4 Chuyển tiếp dòng chảy

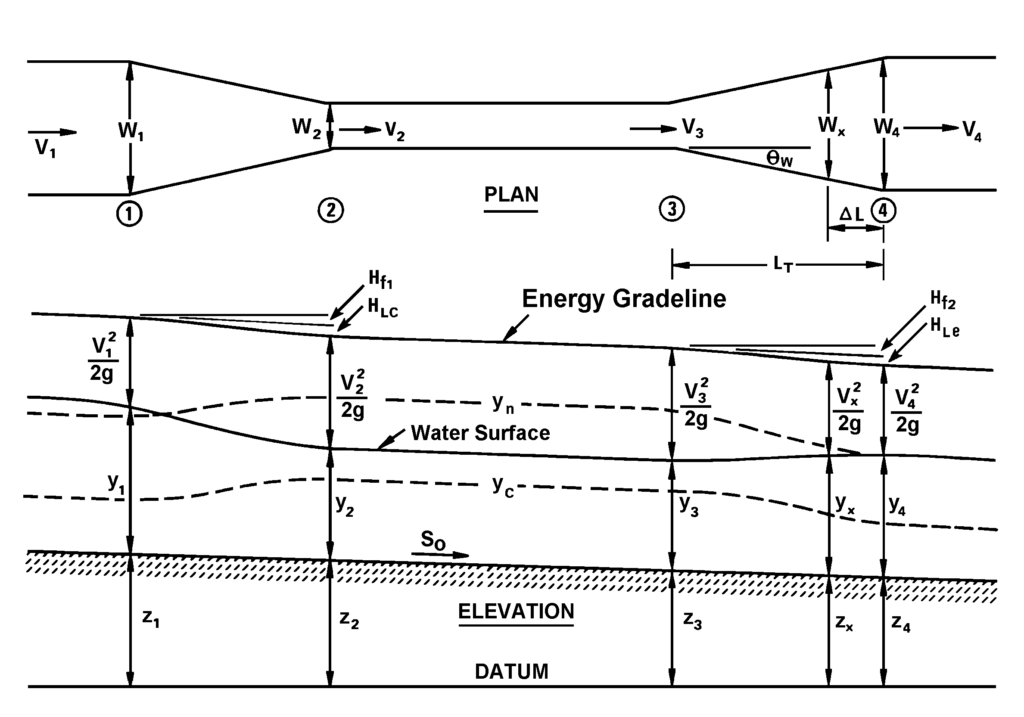
Chuyển tiếp dòng chảy là sự thay đổi mặt cắt dòng chảy kênh hở được thiết kế để thực hiện trong một khoảng cách ngắn với sự xáo trộn dòng chảy tối thiểu. Có năm loại chuyển tiếp được thể hiện trong Hình 4.1: cylindrical quadrant (tứ nón), straight line (đường thẳng), square end (đầu vuông), warped (uốn cong), và wedge (hình nêm). Các hình minh họa là cho trường hợp mở rộng dòng, tuy nhiên các chuyển tiếp thu hẹp dòng sẽ có hình học tương tự.

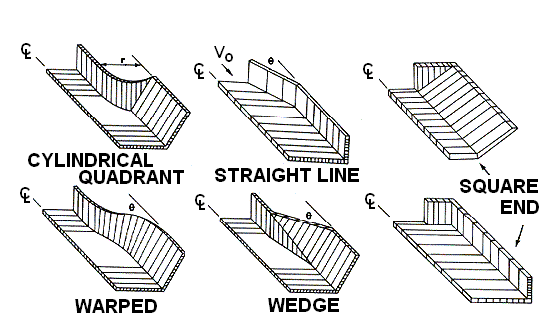
Hình 4.1: Các loại chuyển tiếp

Các loại chuyển tiếp phổ biến nhất là loại square end và mở rộng dòng chảy dạng headwall, cùng với loại tường cánh (straight-line wingwall). Cả hai đều được coi là chuyển tiếp đột ngột và được thảo luận trong Mục 4.1. Các quy trình được cung cấp để xác định vận tốc và độ sâu tại điểm ra của các cấu hình tường đầu tiêu chuẩn này. Một sân đệm (apron), là phần không thể thiếu của các chuyển tiếp này, sẽ bảo vệ đáy kênh tại cửa ra của cống khỏi bị xói lở.

Các chuyển tiếp dòng hở ở miệng vào (thu hẹp) được thiết kế đặc biệt thường không cần thiết đối với cống thoát nước đường bộ. Cống được thiết kế kinh tế để hoạt động với một vùng nước dâng đầu vào (headwater) phía thượng lưu giúp tiêu tán vận tốc dòng chảy tiếp cận và do đó loại bỏ nhu cầu về chuyển tiếp dòng tiếp cận. Các miệng vào cống dạng “thuôn bên” và “thuôn dốc” được thiết kế như các chuyển tiếp ngập nước và không thuộc phạm vi các chuyển tiếp dòng hở được bàn luận trong chương này (xem Normann và các cộng sự, 2001). Các chuyển tiếp miệng vào đặc biệt trở nên hữu ích khi cần thiết phải bảo toàn năng lượng, chẳng hạn do các giới hạn về mức nước dâng đầu vào như trong các công trình tưới tiêu vận hành dưới chế độ dòng chảy dưới tới hạn (xem Mục 4.2), hoặc trong các trường hợp cần duy trì tiết diện nhỏ với dòng chảy siêu tới hạn trong một kênh dốc (xem Mục 4.3). Mục 4.4 bàn về sự mở rộng của dòng chảy siêu tới hạn.

Chuyển tiếp/mở rộng dòng phía thượng lưu của stillings basins (bể tiêu năng) được thiết kế để làm giảm độ sâu dòng chảy, tăng vận tốc, do đó làm tăng số Froude. Các mở rộng siêu tới hạn này bao gồm thiết kế máng dốc và xác định độ hạ thấp cần thiết của đáy suối nhằm ép dòng hình thành cú nhảy thủy lực hiệu quả. Chủ đề này được thảo luận chi tiết tại Mục 8.1.

4.1 Mở rộng đột ngột

Khi một tia nước, không bị giới hạn theo phương ngang, rời khỏi một cống có dòng chảy oulet control, mặt nước sẽ rơi xuống hoặc giảm rất nhanh (xem Hình 4.2). Khi mặt nước giảm xuống và dòng chảy lan rộng, thế năng được lưu trữ dưới dạng độ sâu sẽ chuyển thành động năng hoặc vận tốc. Do đó, vận tốc rời khỏi apron của tường cánh có thể lớn hơn vận tốc tại cửa ra của cống và cần được xem xét trong việc xác định các biện pháp bảo vệ cửa ra. Chuyển tiếp dạng straight-line wingwall cũng có thể được xem là mở rộng đột ngột nếu tan⁡θ lớn hơn 1/3Fr, trong đó θ là góc giữa tường cánh và trục cống.

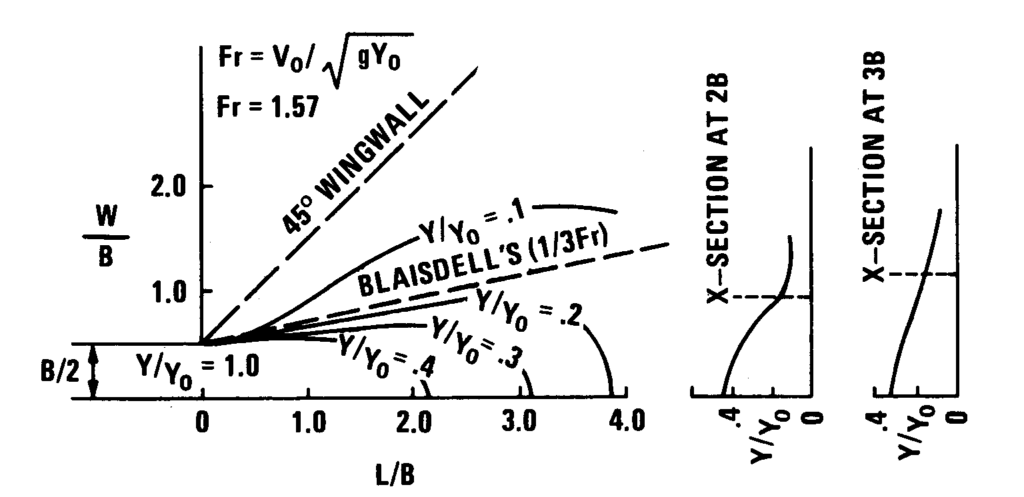
Một cách ước tính hợp lý vận tốc ra tại điểm chuyển tiếp có thể đạt được bằng cách sử dụng phương trình năng lượng và giả định tổn thất không đáng kể. Khi bỏ qua tổn thất do ma sát, một vận tốc cao hơn so với thực tế sẽ được dự đoán, điều này làm cho sai số trở nên an toàn hơn.

Một cách xác định chính xác hơn điều kiện dòng chảy tại điểm ra của chuyển tiếp đã được phát triển bởi Watts (1968). Dữ liệu thực nghiệm của Watts đã được chuyển đổi thành Phương trình 4.1 (cho cống hộp) và Phương trình 4.2 (cho cống tròn) để xác định tỉ số V_A/V₀.

$$\frac{V_A}{V_0} = 1.65 – 0.3Fr \tag{4.1}$$

$$\frac{V_A}{V_0} = 1.65 – 0.45 \left( \frac{Q}{\sqrt{gD^5}} \right) \tag{4.2}$$

trong đó:

• V_A = vận tốc trung bình trên sân đệm (apron), m/s (ft/s)
• V₀ = vận tốc tại cửa ra của cống, m/s (ft/s)

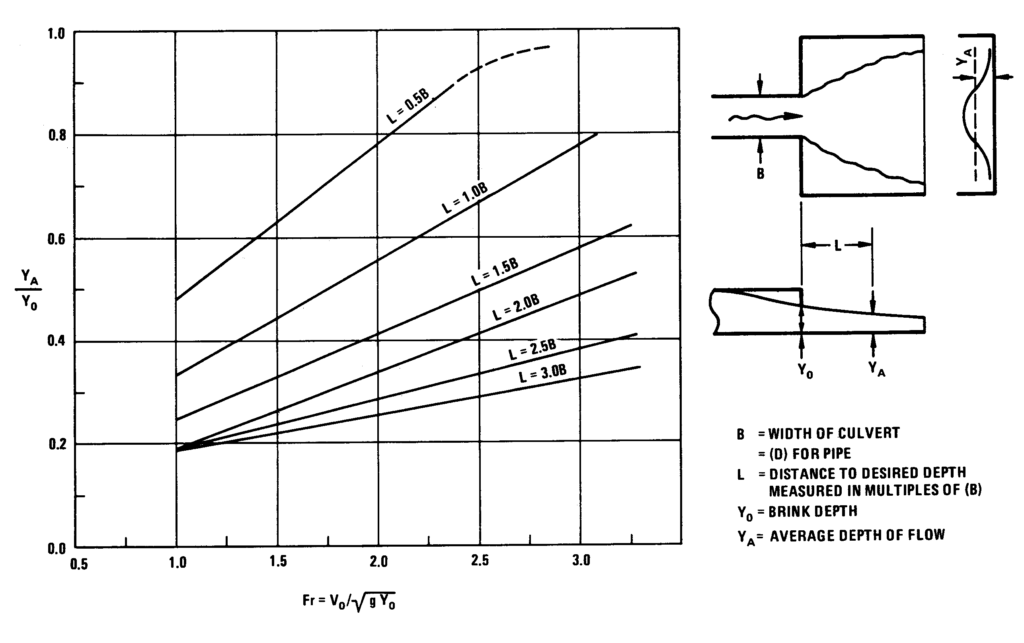
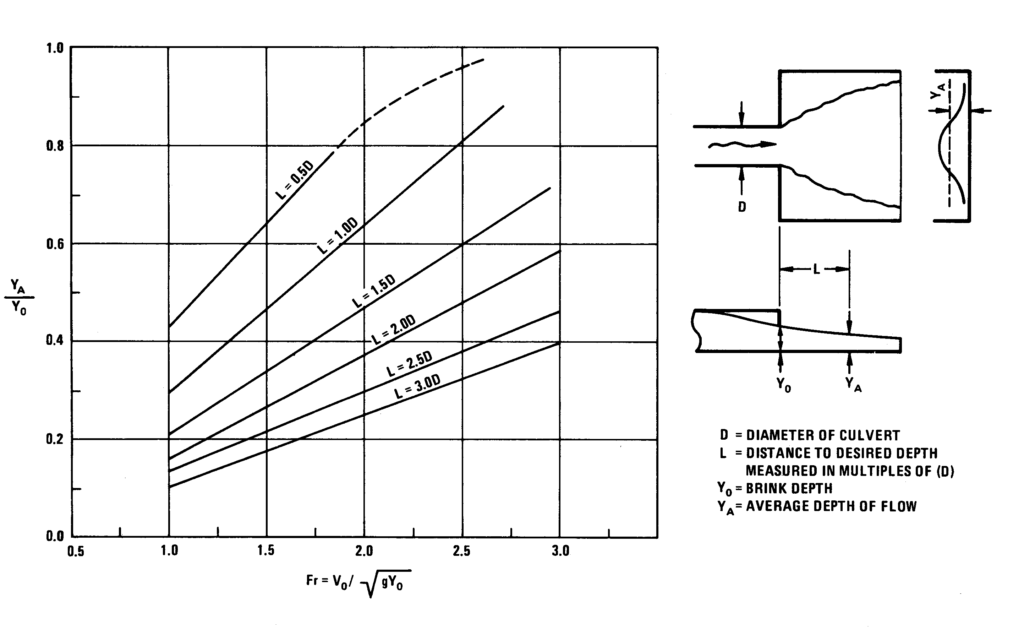
Cũng dựa trên nghiên cứu của Watts, Hình 4.3 và 4.4 liên hệ số Froude (Fr) hoặc Q/(gD⁵)^0.5 với tỷ lệ độ sâu trung bình/độ sâu brink (y_A/y₀). Các phương trình và đường cong này được phát triển cho giá trị Fr từ 1 đến 3, phù hợp với hầu hết các chuyển tiếp cửa ra cống kiểu mở rộng đột ngột. Thông thường, mực nước hạ lưu thấp xảy ra tại cửa ra của cống và dòng chảy là siêu tới hạn trên apron tại cửa ra.

Nước không thể mở rộng hoàn toàn để lấp đầy tiết diện giữa các tường cánh trong một vùng mở rộng đột ngột. Phần lớn dòng chảy sẽ giữ trong một vùng có ranh giới được xác định bởi:

$$\theta = \tan^{-1} \left(\frac{Fr}{3} \right) \tag{4.3}$$

trong đó,
  θ = góc loe tối ưu

Chiều rộng của apron (sân đệm) ở hạ lưu, W₂, được cho bởi:

$$W_2 = W_0 + 2L \tan \theta_w \tag{4.4}$$

trong đó,
  W₂ = chiều rộng apron tại vị trí cách cửa ra của cống một khoảng L (m hoặc ft)
  L  = khoảng cách từ cửa ra cống đến điểm xét (m hoặc ft)
  θ_w = góc loe của tường cánh

Nếu θ_w>θ thì người thiết kế nên xem xét giảm θ_w về θ. Như thể hiện trong Hình 4.2, loe tường cánh nhiều hơn 1/3Fr (ví dụ 45°) sẽ tạo ra vùng không gian không được dòng nước lấp đầy hoàn toàn.

Quy trình thiết kế cho vùng mở rộng đột ngột có thể được tóm tắt như sau:

Bước 1. Xác định điều kiện dòng chảy tại cửa ra cống: V₀ và y₀ (xem Chương 3).

Bước 2. Tính số Froude: \(Fr = V_0 / \sqrt{g y_0}\) tại cửa ra cống.

Bước 3. Tìm góc loe tối ưu, θ, sử dụng Phương trình 4.3. Nếu góc loe tường cánh chọn ban đầu θ_w lớn hơn θ, hãy xem xét giảm θ_w về θ.

Bước 4. Tìm độ sâu trung bình trên apron. Đối với tiết diện hình hộp, sử dụng Hình 4.3. Đối với ống tròn, sử dụng Hình 4.4. Tỷ lệ y_A/y₀ thu được dựa trên số Froude (Fr) và khoảng cách mong muốn đến hạ lưu L.

Bước 5. Tìm vận tốc trung bình trên apron, V_A, sử dụng Phương trình 4.1 hoặc 4.2. V_A=V₂

Bước 6. Tính chiều rộng hạ lưu, W₂, sử dụng Phương trình 4.4.

Bước 7. Tính độ sâu hạ lưu, y₂:
 - Nếu θ được dùng trong Phương trình 4.4, thì:
  \(y_2 = Q / (V_A W_2)\). Độ sâu này sẽ lớn hơn y_A vì dòng chảy hiện tại được giới hạn theo phương ngang.

 - Nếu θ_w được dùng trong Phương trình 4.4, thì \(y_2 = y_A\). Tuy nhiên, hãy ước lượng chiều rộng dòng chảy thực tế \(W_A = Q / (V_A y_A)\). Kiểm tra xem \(W_A < W_2\). Nếu không, thì:
  \(y_2 = Q / (V_A W_2).\)

Ví dụ thiết kế: Chuyển tiếp mở rộng đột ngột (đơn vị SI)

Tìm điều kiện dòng chảy (y₂ và V₂) tại cuối apron dài 3.1 m. Giả định mực nước hạ lưu (tailwater) không đáng kể.

Cho:

• RCB = 1524 mm × 1524 mm (cống hộp BTCT)
• Góc loe tường cánh \(\theta_w = 45^\circ\)
• Chiều dài cống = 61 m
• Độ dốc đáy cống \(S_o = 0.002 \, \text{m/m}\)
• Lưu lượng \(Q = 7.65 \, \text{m}^3/\text{s}\)
• Độ sâu tới hạn \(y_c = 1.37 \, \text{m}\)

Giải:

Bước 1. Tìm vận tốc tại cửa ra cống từ Hình 3.3 với TW/D ≈ 0
Cần giá trị:

$$1.811 \cdot \frac{Q}{BD^{3/2}} = 1.811 \cdot \frac{7.65}{(1.524)(1.524)^{3/2}} = 4.83$$

$$\frac{y_0}{D} = 0.68 \Rightarrow y_0 = 0.68 \cdot 1.524 = 1.036 \, m$$

$$V_0 = \frac{Q}{A} = \frac{7.65}{(1.036)(1.524)} = 4.84 \, m/s$$

Bước 2. Tính số Froude tại cửa ra:

$$Fr = \frac{V_0}{\sqrt{g y_0}} = \frac{4.84}{\sqrt{9.81 \cdot 1.036}} = 1.52$$

Bước 3. Tìm góc loe tối ưu θ:

$$\tan\theta = \frac{1}{3Fr} = \frac{1}{3(1.52)} = 0.22 \Rightarrow \theta = 12.37^\circ$$

Bước 4. Ước lượng độ sâu trung bình:

Tỷ lệ chiều dài apron / đường kính cống: \(\frac{3.1}{1.524} \approx 2\)

Từ Hình 4.3, với \(y_A / y_0 = 0.26\): \(y_A = 0.26 \cdot 1.036 = 0.269 \, m\)

Bước 5. Tìm vận tốc trung bình trên apron V_A, dùng Phương trình 4.1:

$$\frac{V_A}{V_0} = 1.65 – 0.3Fr = 1.65 – 0.3(1.52) = 1.2$$

$$V_A = 4.84 \cdot 1.2 = 5.82 \, m/s \Rightarrow V_A = V_2 = 5.82 \, m/s$$

Bước 6. Tính chiều rộng hạ lưu W₂ dùng Phương trình 4.4
Vì \(\theta_w > \theta\), nên dùng \(\theta_w\):

$$W_2 = W_0 + 2L \tan(\theta_w) = 1.524 + 2(3.1)(1.0) = 7.72 \, m$$

Bước 7. Tính độ sâu hạ lưu y₂:
Vì dùng \(\theta_w\), nên: \(y_2 = y_A = 0.269 \, m\)

Kiểm tra chiều rộng thực tế dòng chảy \(W_A\):

$$W_A = \frac{Q}{V_A \cdot y_A} = \frac{7.65}{5.82 \cdot 0.269} = 4.89 \, m < 7.72 \, m$$

→ Thỏa mãn điều kiện chiều rộng dòng nhỏ hơn apron.

So sánh lời giải ở trên với hai phương án sử dụng phương trình năng lượng.

Phương án 1. Giả sử W₂ bằng toàn bộ khoảng cách giữa hai tường cánh tại cuối apron:

$$W_2 = W_0 + 2L \tan 45^\circ = 7.72 \, m$$

$$A_2 = W_2 \cdot y_2 = 7.72 \cdot y_2$$

$$V_2 = Q / A_2 = 7.65 / (7.72 \cdot y_2) = 0.99 / y_2$$

Cân bằng năng lượng giữa dòng chảy tại cửa ra cống và apron:

$$z_0 + y_0 + \frac{V_0^2}{2g} = z_2 + y_2 + \frac{V_2^2}{2g} + H_f$$

Giả sử \(H_f = 0\) và \(z_0 = z_2\), ta có:

$$1.036 + \frac{(4.84)^2}{2 \cdot 9.81} = y_2 + \frac{(0.99)^2}{2 \cdot 9.81 \cdot y_2^2}$$

$$1.036 + 1.194 = y_2 + \frac{0.050}{y_2^2}$$

$$2.230 = y_2 + \frac{0.050}{y_2^2}$$

→ Giải ra:

$$y_2 = 0.157 \, m \quad (\text{thấp hơn 41% so với lời giải ban đầu})$$

$$V_2 = 0.99 / 0.157 = 6.31 \, m/s \quad (\text{cao hơn 8% so với lời giải ban đầu})$$

Phương án 2. Giả sử \(W_2\) được tính theo góc loe tối ưu với \(\tan \theta = 1 / (3 Fr)\)

$$W_2 = W_0 + 2L \tan 12.41^\circ = 1.524 + 6.2 \cdot 0.22 = 2.89 \, m$$

$$A_2 = 2.89 \cdot y_2 \quad \Rightarrow \quad V_2 = 7.65 / (2.89 \cdot y_2) = 2.65 / y_2$$

Cân bằng năng lượng:

$$2.230 = y_2 + \frac{0.360}{y_2^2}$$

→ Giải ra:

$$y_2 = 0.45 \, m \quad (\text{cao hơn 68% so với lời giải ban đầu})$$

$$V_2 = 2.65 / 0.45 = 5.89 \, m/s \quad (\text{cao hơn 2% so với lời giải ban đầu})$$

4.2 Chuyển tiếp dòng chảy dưới tới hạn (Subcritical Flow Transition)

Dòng chảy dưới tới hạn có thể được chuyển tiếp vào và ra khỏi các công trình mà không gây ảnh hưởng xấu nếu trạng thái dòng dưới tới hạn được duy trì xuyên suốt công trình. Dòng chảy không được tiếp cận hoặc vượt qua độ sâu tới hạn y_c. Phạm vi độ sâu cần tránh là từ 0.9 y_c đến 1.1y_c. Trong phạm vi này, các thay đổi nhỏ về năng lượng riêng sẽ tạo ra thay đổi lớn về độ sâu, tức là có thể phát sinh sóng hoặc dao động dòng chảy.

Loại chuyển tiếp straight line hoặc wedge nên được sử dụng nếu cần bảo toàn năng lượng dòng, ví dụ như trong hệ thống kênh tưới tiêu băng qua đường. Chuyển tiếp dạng cong (warped) và tứ nón (cylindrical) hiệu quả hơn, nhưng chi phí xây dựng cao hơn chỉ có thể biện minh khi cấu trúc phải chịu ảnh hưởng đáng kể từ backwater.

Hình 4.5 minh họa bài toán thiết kế: Dòng chảy bắt đầu ở thượng lưu của tiết diện 1, nơi có thể có hiện tượng backwater phía trước cống, dòng được chuyển tiếp từ kênh vào trong và ra khỏi cống. Góc loe θ_w nên là 12.5°, tương ứng với tỉ lệ 1:4.5 (ngang:dọc) hoặc nhỏ hơn theo Hinds (1928). Tiêu chí này cung cấp một chuyển tiếp biến đổi dần mà có thể được phân tích bằng phương trình năng lượng.

Khi dòng chảy chuyển tiếp vào cống, mặt nước sẽ tiệm cận y_c. Để giảm thiểu sóng, y₂ nên bằng hoặc lớn hơn 1.1y_c. Trong cống, độ sâu sẽ tăng và đạt y_n nếu chiều dài cống đủ dài. Trong vùng mở rộng, độ sâu sẽ tăng lên đến y_n của kênh hạ lưu (xem Phần 4). Cả hai dạng chuyển tiếp đều liên quan đến tổn thất năng lượng tỉ lệ với sự thay đổi động năng trong các chuyển tiếp. Tổn thất năng lượng tại phần thu hẹp \(H_{Lc}\), và phần mở rộng \(H_{Le}\), được tính như sau:

$$H_{Lc} = C_c \left( \frac{V_2^2}{2g} – \frac{V_1^2}{2g} \right) \tag{4.5}$$

$$H_{Le} = C_e \left( \frac{V_3^2}{2g} – \frac{V_4^2}{2g} \right) \tag{4.6}$$

trong đó C_c và C_e được lấy từ Bảng 4.1.

Bảng 4.1. Hệ số tổn thất chuyển tiếp (USACE, 1994)

Loại chuyển tiếp	Cc (thu hẹp)	Ce (mở rộng)
Warped (cong)	0.10	0.20
Cylindrical Quadrant (tứ nón)	0.15	0.25
Wedge (nêm)	0.30	0.50
Straight Line (đường thẳng)	0.30	0.50
Square End (đầu vuông)	0.30	0.75

Độ sâu trong cống, y₃, có thể được tìm bằng phương pháp thử và sai sử dụng phương trình năng lượng, với giả định y₄ = y_n tại kênh hạ lưu và \(H_{f2} = 0\) (xem Hình 4.5). Cao độ dòng tại tiết diện 2 là z₂. Viết phương trình năng lượng giữa đoạn 3 và 4:

$$z_4 + y_4 + \frac{V_4^2}{2g} + H_{Le} + H_{f2} = z_3 + y_3 + \frac{V_3^2}{2g}$$

Giả sử \(H_{f2} = 0\), \(V_3 = Q / (W_3 y_3)\), \(V_4 = Q / (W_4 y_4)\), và thay thế phương trình (4.6), ta có:

$$z_4 + y_4 + \frac{V_4^2}{2g} + C_e \left( \frac{V_3^2}{2g} – \frac{V_4^2}{2g} \right) = z_3 + y_3 + \frac{V_3^2}{2g}$$

$$z_4 + y_4 + (1 – C_e) \frac{V_4^2}{2g} = z_3 + y_3 + (1 – C_e) \frac{V_3^2}{2g}$$

$$z_4 – z_3 + y_4 + (1 – C_e) \frac{Q^2}{2g (W_4 y_4)^2} = y_3 + (1 – C_e) \frac{Q^2}{2g (W_3 y_3)^2} \tag{4.7}$$

Khi thay các giá trị đã biết vào, phương trình (4.7) được rút gọn thành:

$$C_1 = y_3 + \frac{C_2}{y_3^2}$$

Phương trình này có thể được giải bằng phương pháp thử và sai.

Tương tự như vậy, y₁ có thể được xác định bằng cách giả sử \(y_2 = y_3\) và \(h_{f1} = 0\).

$$z_2 + y_2 + \frac{V_2^2}{2g} + H_{Lc} + H_{f1} = z_1 + y_1 + \frac{V_1^2}{2g}$$

$$z_2 + y_2 + \frac{V_2^2}{2g} + C_c \left( \frac{V_2^2}{2g} – \frac{V_1^2}{2g} \right) = z_1 + y_1 + \frac{V_1^2}{2g}$$

$$z_2 + y_2 + (1 + C_c)\frac{V_2^2}{2g} = z_1 + y_1 + (1 + C_c)\frac{V_1^2}{2g}$$

$$z_2 – z_1 + y_2 + (1 + C_c)\frac{Q^2}{(W_2 y_2)^2 \cdot 2g} = y_1 + (1 + C_c)\frac{Q^2}{(W_1 y_1)^2 \cdot 2g} \tag{4.8}$$

Các độ sâu trên chỉ là gần đúng vì đã bỏ qua tổn thất do ma sát.
Chúng nên được kiểm tra lại bằng cách tính toán biên dạng mặt nước sử dụng phương pháp bước tiêu chuẩn (standard step method) trong phần mềm chuyên dụng như HEC-RAS (USACE, 2002).

4.3 Thu hẹp dòng siêu tới hạn (Supercritical Flow Contraction)

Thiết kế chuyển tiếp cho dòng chảy siêu tới hạn rất khó kiểm soát nếu không gây ra hiện tượng nhảy thủy lực (hydraulic jump) hoặc bất thường trên bề mặt dòng chảy. Do đó, nên duy trì tiết diện chảy đầy nếu có thể.

Chuyển tiếp êm đối với dòng siêu tới hạn yêu cầu kết cấu tường cánh dài hơn thông thường, và không nên thực hiện nếu công trình không thật sự quan trọng. Nên tiến hành nghiên cứu mô hình để xác định hình học chuyển tiếp trong trường hợp không muốn xảy ra nhảy thủy lực. Nếu nhảy thủy lực có thể chấp nhận, thì cấu trúc cửa vào có thể được thiết kế như Hình 4.6.

Thiết kế này chỉ áp dụng cho kênh hình chữ nhật, và cho chuyển tiếp kéo dài. Cách tiếp cận thiết kế được trích từ USACE (1994) và Ippen (1951).

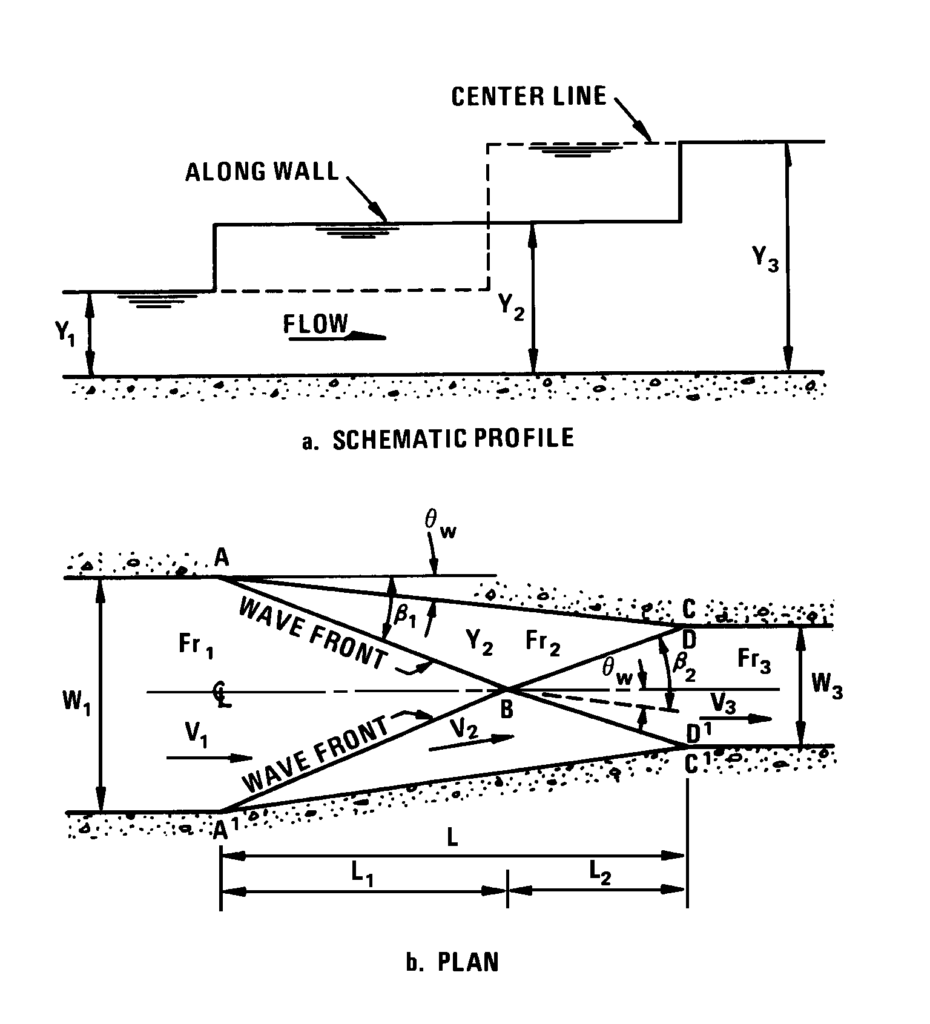
Chiều dài, L, được xác định bởi độ thu hẹp của kênh, \(W_1 – W_3\), và góc lệch tường \(\theta_w\):

$$L = \frac{(W_1 – W_3)}{2 \tan \theta_w} \tag{4.9}$$

Để giảm thiểu nhiễu loạn bề mặt, L cũng nên bằng \(L_1 + L_2\), trong đó:

$$L_1 = \frac{W_1}{2 \tan \beta_1} \tag{4.10}$$

$$L_2 = \frac{W_3}{2 \tan (\beta_2 – \theta_w)} \tag{4.11}$$

$$\tan \theta_w = \frac{\tan \beta_1 \left( \sqrt{1 + 8 Fr_1^2 \sin^2 \beta_1} – 3 \right)}{2 \tan^2 \beta_1 + \sqrt{1 + 8 Fr_1^2 \sin^2 \beta_1} – 1} \tag{4.12}$$

Thiết kế chuyển tiếp yêu cầu một giá trị thử \(\theta_w\) cố định L theo phương trình (4.9). Chiều dài này sau đó được kiểm tra bằng cách tính \(L_1 + L_2\).

Để xác định \(L_1\), \(\beta_1\) được tìm bằng phương pháp thử và sai từ phương trình (4.12) và sau đó thay vào phương trình (4.10).

\(L_2\) được tính từ phương trình (4.11) với \(\beta_2\) được xác định bằng phương trình (4.12), thay \(\beta_2\) vào thay cho \(\beta_1\), và \(Fr_1\) thay bằng \(Fr_2\). Để tìm \(2Fr_2\), đầu tiên tính:

$$\frac{y_2}{y_1} = \frac{1}{2} \left( \sqrt{1 + 8 Fr_1^2 \sin^2 \beta_1} – 1 \right) \tag{4.13}$$

Sau đó:

$$\text{Fr}_2^2 = \frac{y_1}{y_2} \left[ \text{Fr}_1^2 – \left( \frac{y_1}{2y_2} \right) \left( \frac{y_2}{y_1} – 1 \right) \left( \frac{y_2}{y_1} + 1 \right)^2 \right]\tag{4.14}$$

Nếu giá trị thử \(\theta_w\) được chọn đúng, tổng chiều dài L sẽ bằng \(L_1 + L_2\). Nếu không, chọn lại một giá trị thử khác cho \(\theta_w\) và lặp lại quá trình cho đến khi các chiều dài khớp nhau.

Độ sâu \(y_3\), và \(Fr_3\) trong cống có thể được tính bằng phương trình (4.13) và (4.14) nếu thay chỉ số tương ứng. Ví dụ, \(y_2 / y_1\) sẽ là \(y_3 / y_2\).

Thiết kế trên giả định rằng chiều rộng của kênh (\(W_1\)) và cống (\(W_3\)) đã biết, và L được tìm qua phương pháp thử và sai. Nếu W₃ chưa biết, bài toán sẽ phức tạp hơn vì phải dùng thêm một quá trình thử và sai.

4.4 Mở rộng dòng siêu tới hạn (Supercritical Flow Expansion)

Thiết kế mở rộng dòng chảy siêu tới hạn đã được bàn đến một phần trong Mục 4.1. Quy trình được nêu trong Mục 4.1 nên được sử dụng để xác định điều kiện dòng chảy tại apron hoặc vùng mở rộng, nếu số Froude tại cửa ra của cống, Fr, nhỏ hơn 3, vị trí cần xác định điều kiện dòng nằm trong phạm vi 3 đường kính cống tính từ cửa ra, và độ dốc đáy \(S_o\) nhỏ hơn 10%.

Đối với các vùng mở rộng ngoài các giới hạn trên, phương trình năng lượng có thể được sử dụng để xác định điều kiện dòng rời khỏi vùng chuyển tiếp. Thông thường, các tham số này sẽ được dùng làm giá trị đầu vào cho thiết kế bể tiêu năng (basin).