9. Streambed Level Dissipators (Cấu trúc tiêu năng ở đáy suối)

Chương này bao gồm các cấu trúc tiêu năng cho cửa xả cống được thiết kế để hoạt động tại mực đáy dòng suối và khôi phục lại điều kiện dòng chảy tự nhiên ở hạ lưu từ cửa xả cống. Chúng cũng được thiết kế để thoát nước bằng trọng lực khi không vận hành. Các phần sau trình bày giới hạn, hướng dẫn thiết kế và ví dụ thiết kế cho các cấu trúc tiêu năng sau:

• Bể thành cứng của Đại học Bang Colorado (CSU)
• Bể Contra Costa
• Bể Hook
• Bể va Type VI của Cục Khai hoang Hoa Kỳ (USBR)

9.1 Bể thành cứng CSU

Bể thành cứng của Đại học Bang Colorado (CSU), minh họa trong Hình 9.1, sử dụng các hàng phần tử gồ so le để tạo ra nhảy thủy lực (Simons, 1970). CSU đã thử nghiệm một số bể với các cấu hình gồ khác nhau để xác định hệ số cản trung bình trên phần đáy gồ của bể. Ảnh hưởng của các phần tử gồ được phản ánh trong hệ số cản được xác định thực nghiệm đối với mỗi cấu hình. Quy trình thực nghiệm là đo độ sâu và vận tốc tại mỗi đầu của thể tích điều khiển minh họa trong Hình 9.2, và tính hệ số cản của bể, \(C_B\), từ phương trình động lượng bằng cách cân bằng lực tác dụng lên thể tích chất lỏng.

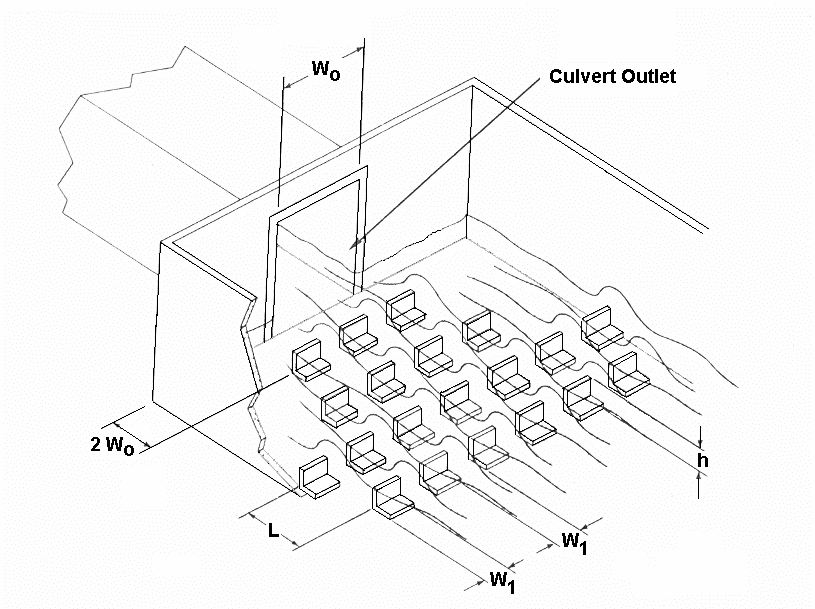
Kết quả thử nghiệm CSU chỉ ra một số giới hạn thiết kế. Chiều cao của các phần tử gồ ghề, hh, phải nằm trong khoảng từ 0.31 đến 0.91 của độ sâu trung bình dòng chảy đến, \(y_A\), và khoảng cách tương đối giữa các hàng phần tử, L/h, phải là 6 hoặc 12. Yêu cầu này không phải là một giới hạn nghiêm ngặt vì khoảng cách tương đối thường là một tham số cố định trong quy trình thiết kế, và các thử nghiệm khác (Morris, 1968) đã cho thấy khoảng từ 6 đến 12 là tốt nhất cho việc tiêu tán năng lượng.

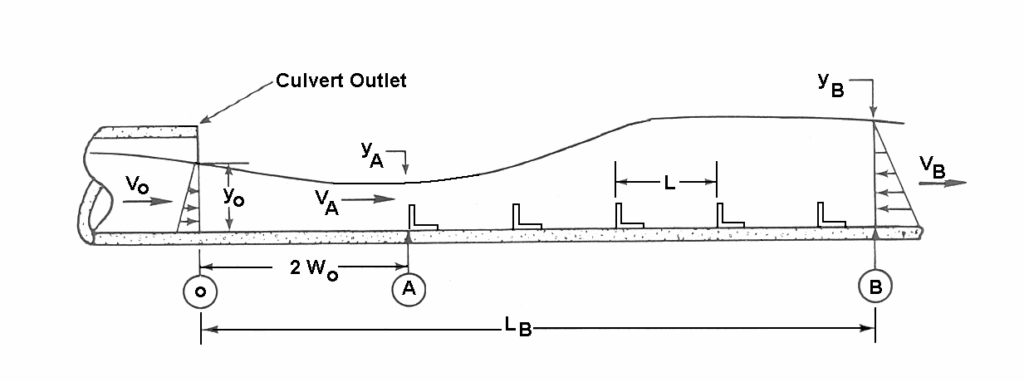
Các cấu hình gồ đã thử nghiệm và kết quả tương ứng cho \(C_B\) được thể hiện trong Hình 9.3 và Bảng 9.1. Để thiết kế một bể, người thiết kế chọn một bể từ Hình 9.3 và sử dụng giá trị \(C_B\) từ Bảng 9.1 trong phương trình động lượng sau để xác định vận tốc trong bể \(V_B\) nếu độ dốc nhỏ hơn 10%:

$$\rho V_0 Q + C_P \gamma \left( \frac{y_0^2}{2} \right) W_0 = C_B A_F N \rho \frac{V_A^2}{2} + \rho V_B Q + \gamma \frac{Q^2}{2 V_B^2 W_B} \tag{9.1}$$

trong đó:

• \(y_0\) = độ sâu tại cửa ra cống, m (ft)
• \(V_0\) = vận tốc tại cửa ra cống, m/s (ft/s)
• \(W_0\) = chiều rộng cống tại cửa ra, m (ft)
• \(V_A\) = vận tốc dòng chảy tại vị trí cách cửa ra hai bề rộng cống, m/s (ft/s)
• \(V_B\) = vận tốc ra, ngay sau hàng cuối cùng của các phần tử gồ, m/s (ft/s)
• \(W_B\) = chiều rộng bể, ngay sau hàng cuối cùng của các phần tử gồ, m (ft)
• N = tổng số phần tử gồ trong bể
• \(A_F\) = diện tích mặt trước của một phần tử gồ ghề, m² (ft²)
• \(C_B\) = hệ số cản của bể (xem Hình 9.3)
• \(C_P\) = hệ số hiệu chỉnh động lượng cho áp lực tại cửa ra cống (xem Hình 9.4)
• γ = trọng lượng riêng của nước, 9810 N/m³ (62.4 lb/ft³)
• ρ = khối lượng riêng của nước, 1000 kg/m³ (1.94 slugs/ft³)

Các giá trị \(C_B\) được liệt kê tương ứng với tỉ lệ mở rộng \(W_B / W_0\), từ 4 đến 8, dựa trên các cấu hình đã thử nghiệm. Các giá trị \(C_B\) phát triển cho cấu hình \(W_B / W_0 = 4\) cũng có thể áp dụng cho các tỉ lệ mở rộng nhỏ hơn 4 nhưng lớn hơn hoặc bằng 2, miễn là cùng số lượng phần tử gồ, N, được đặt trong bể. Với các tỉ lệ mở rộng nhỏ hơn này, có thể cần tăng số hàng, \(N_r\), để đạt được N yêu cầu như thể hiện trong Hình 9.3. Các phần tử trong tất cả các bể đều được bố trí đối xứng qua trục giữa của bể. Tất cả các bể đều được mở loe đến chiều rộng \(W_B\) của bể mở rộng đột ngột tương ứng.

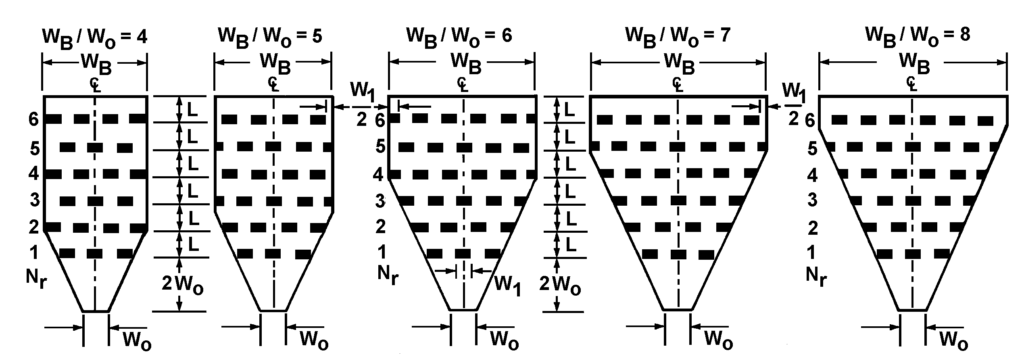
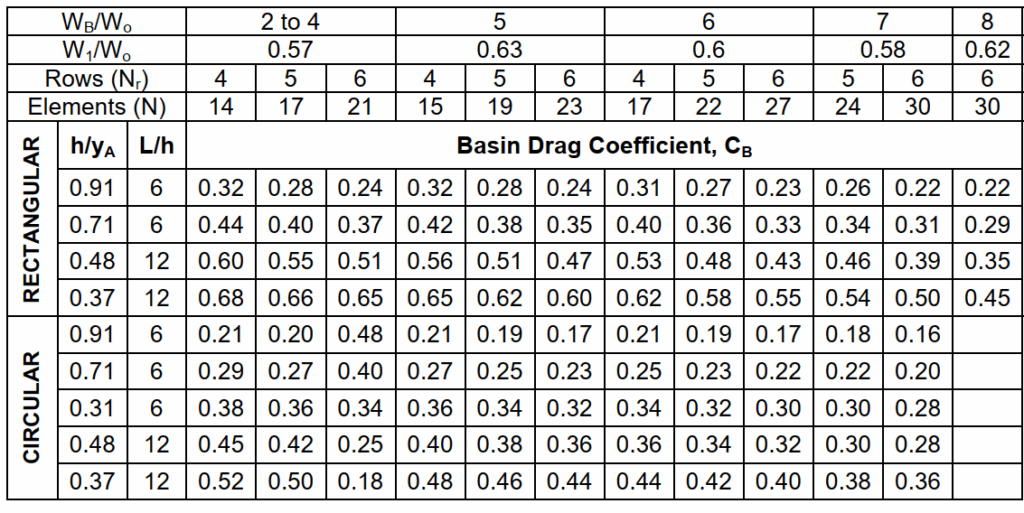
Phương trình 9.1 áp dụng cho các bể có độ dốc nhỏ hơn 10 phần trăm. Với các bể có độ dốc lớn hơn, trọng lượng của nước trong vùng nhảy thủy lực cần được xét đến trong biểu thức. Phương trình 9.2 bao gồm thành phần trọng lượng bằng cách giả định mặt nước thẳng qua vùng nhảy.

$$C_P\, \gamma\, y_0^2\, W_0 / 2 + \rho\, V_0 Q + w\, (\sin\theta) = C_B\, A_F\, N\, \rho\, V_A^2 / 2 + \gamma\, Q^2 / (2 V_B^2 W_B) + \rho\, V_B Q \tag{9.2}$$

trong đó:

w = trọng lượng nước trong bể

\(\text{Thể tích} = (y_0 W_0 + y_A W_A) W_0 + \left( \frac{0.75 L Q}{V_B} \right) \left[ (N_r – 1) – \left( \frac{W_B}{W_0} – 3 \right) \left( 1 – \frac{W_A}{W_B} \right)/2 \right]\)

\(\text{Trọng lượng} = \text{Thể tích} \cdot \gamma\)

θ = arc tan của độ dốc kênh, \(S_o\)
\(N_r\) = số hàng phần tử gồ
L = khoảng cách dọc giữa các hàng phần tử

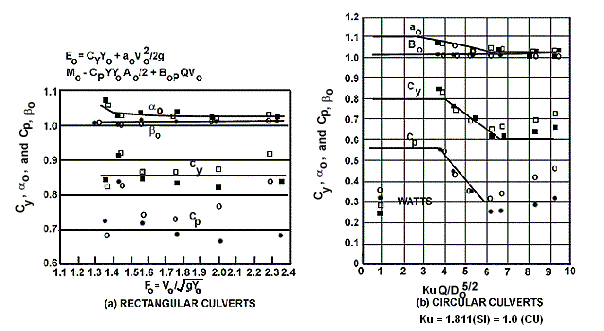
Độ sâu \(y_A\) tại đầu các phần tử gồ ghề có thể được xác định từ Hình 4.3 và Hình 4.4. Các hình này dựa trên các độ dốc nhỏ hơn 10 phần trăm. Vận tốc \(V_A\) có thể được tính bằng các Phương trình 4.1 hoặc 4.2. Khi độ dốc lớn hơn 10 phần trăm, \(V_A\) và \(y_A\) có thể được tính bằng phương trình năng lượng sau đây, viết giữa cuối cống (điểm o) và vị trí cách cửa xả hai lần chiều rộng cống (điểm A):

$$2W_0 S_0 + y_A + 0.25 \left( \frac{Q}{W_A y_A} \right)^2 / (2g) = y_0 + 0.25 \left( \frac{V_0^2}{2g} \right) \tag{9.3}$$

trong đó:
\(W_A = W_0 \left[ \frac{4}{3Fr} + 1 \right]\) (được điều chỉnh từ Phương trình 4.3 và 4.4)

Việc bắn tung nước qua hàng đầu tiên của các phần tử gồ sẽ xảy ra nếu các phần tử quá lớn và vận tốc dòng đến cao. Vấn đề này có thể được giải quyết bằng cách đặt thiết bị tiêu năng một phần hoặc toàn bộ bên trong thân cống, cung cấp khoảng trống (freeboard) đủ trong vùng hắt nước, hoặc cung cấp tấm chắn hắt nước. Nếu khả thi cả về kết cấu lẫn thủy lực, việc đặt thiết bị tiêu năng một phần hoặc toàn bộ bên trong thân cống có thể mang lại lợi ích về kinh tế, an toàn và thẩm mỹ.

Khoảng trống yêu cầu (freeboard) có thể được xác định từ:

$$FB = h + y_A + 0.5 (V_A \sin \phi)^2 / g \tag{9.4}$$

trong đó:
FB = khoảng trống (freeboard) cần thiết, m (ft)
h = chiều cao phần tử gồ ghề, m (ft)
\(y_A\) = độ sâu dòng đến trước hàng phần tử đầu tiên, m (ft)
g = 9.81 m/s² (32.2 ft/s²)
\(\phi = 45^\circ\) (là hàm của \(y_A/h\) và số Froude, nhưng chưa có quan hệ cụ thể được xác lập)

ϕ được cho là phụ thuộc vào tỉ lệ \(y_A/h\) và số Froude, nhưng chưa có mối quan hệ cụ thể được thiết lập. Góc 45° là một xấp xỉ hợp lý.

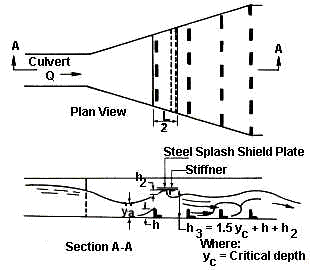
Một giải pháp khác là tấm chắn hắt nước (splash shield), đã được nghiên cứu tại Phòng Thí nghiệm Thủy lực FHWA bởi J.S. Jones (nghiên cứu chưa công bố). Tấm chắn hắt là một tấm có thanh tăng cứng được treo giữa hai hàng phần tử gồ đầu tiên như minh họa trong Hình 9.5. Chiều cao tấm được chọn khá tùy ý như một hàm của độ sâu tới hạn vì dòng thường chuyển qua trạng thái tới hạn gần các phần tử gồ lớn.

Mặc dù các thử nghiệm được thực hiện với các cấu hình mở rộng đột ngột, nhưng cấu hình được khuyến nghị sử dụng là các bể mở loe–mở rộng kết hợp như thể hiện trong Hình 9.3 và các hình phía trên. Các bể này chứa cùng số lượng phần tử gồ ghề như bể mở rộng đột ngột. Góc mở loe, \(u_e\), là một hàm của khoảng cách dọc giữa các hàng phần tử, L, và chiều rộng cống,

$$u_e = \frac{4}{7} + \left(\frac{10}{7}\right)\frac{L}{W_0} \tag{9.5}$$

Quy trình thiết kế cho bể thành cứng CSU có thể được tóm tắt như sau:

Bước 1.
Tính vận tốc \(V_0\), độ sâu \(y_0\), và số Froude Fr tại cửa ra cống, hoặc nếu bể được đặt một phần hay toàn bộ trong thân cống, thì tại phần mở loe của thân cống.

Bước 2.
Chọn một bể từ Bảng 9.1 dựa trên tỷ lệ mở rộng \(W_B / W_0\) phù hợp nhất với hình học thực tế hoặc đáp ứng các ràng buộc khác. Chọn \(W_B / W_0\), số hàng \(N_r\), số phần tử N, và các tỷ lệ \(h / y_A\) vàhL/h.

Bước 3.
Xác định điều kiện dòng \(V_A\) và \(y_A\) tại vị trí dòng tiếp cận vùng phần tử gồ (cách cửa xả hai lần chiều rộng cống).

• Tính \(V_A\) bằng Phương trình 4.1 hoặc 4.2
• Với \(4 < W_B/W_0 < 8\), đọc \(y_A\) từ Hình 4.3 và 4.4
• Với \(W_B / W_0 < 4\), tính \(y_A\) bằng Phương trình 9.3
• Với độ dốc > 10%, dùng Phương trình 9.3 để tìm cả \(V_A\) và \(y_A\)

Bước 4.
Với giá trị thử nghiệm của tỷ lệ chiều cao phần tử gồ trên độ sâu dòng đến \(h / y_A \)và tỷ lệ chiều dài trên chiều cao L/h, xác định các thông số tiêu năng từ Hình 9.3:
a. chiều cao phần tử gồ ghề h
b. khoảng cách dọc giữa các hàng phần tử L
c. chiều rộng bể \(W_B\)
d. chiều rộng phần tử \(W_1\), bằng khoảng cách giữa các phần tử
e. độ mở loe \(u_e\)
f. hệ số cản bể \(C_B\)
g. diện tích mặt trước phần tử gồ \(A_F = W_1 h\)
h. hệ số áp lực \(C_P\) từ Hình 9.4
i. tổng chiều dài bể \(L_B = 2W_0 + L(N_r)\). Điều này đảm bảo phần hạ lưu của hàng phần tử cuối cùng có chiều dài bằng L

Bước 5.
Kiểm tra rằng bể thử nghiệm tạo ra vận tốc ra \(V_B\) và độ sâu \(y_B\) phù hợp với điều kiện hạ lưu.

• Nếu \(W_B\) trùng với chiều rộng kênh hạ lưu hoặc tailwater điều khiển, theo tùy chọn 1
• Nếu \(W_B\) nhỏ hơn chiều rộng kênh, theo tùy chọn 2

Tùy chọn 1:
Sử dụng độ sâu hạ lưu \(y_n\) hoặc tailwater nếu lớn hơn để giải Phương trình 9.1 hoặc 9.2 cho đại lượng \(C_B A_F N\).

• Tính \(C_B A_F N\) cho bể
• Nếu giá trị tính được từ phương trình nhỏ hơn giá trị bể → chọn lại cấu hình gồ

Tùy chọn 2:
Sử dụng \(C_B, A_F\), và N từ Bước 2 và 4 để giải \(V_B\) trong Phương trình 9.1 hoặc 9.2

• Có 3 nghiệm cho \(V_B\): 2 nghiệm dương, 1 âm
• Loại nghiệm âm, thường dùng nghiệm lớn hơn
• Nếu không phù hợp với điều kiện hạ lưu → đổi cấu hình
• Nếu phù hợp → tính \(y_B\)
• Nếu \(y_B < y_n\) → dùng nghiệm nhỏ hơn để tính lại \(y_B\)

Lưu ý:
Nếu tailwater lớn hơn \(y_B\), thì \(V_B\) nên được tính bằng cách sử dụng độ sâu tailwater và bể thử nghiệm được kiểm tra lại theo phương án 1.

Bước 6.
Phác họa bể. Bố trí bể được thể hiện trong Hình 9.3. Các phần tử được bố trí đối xứng qua trục giữa của bể và khoảng cách giữa các phần tử xấp xỉ bằng chiều rộng phần tử. Trong mọi trường hợp, khoảng cách này không được nhỏ hơn 75% chiều rộng phần tử. Tỷ lệ /(W_1 / h\) phải nằm trong khoảng từ 2 đến 8, và ít nhất một nửa số hàng phần tử phải có phần tử nằm gần tường để ngăn dòng tia vận tốc cao đi suốt chiều dài bể. Các hàng nên được sắp lệch nhau để làm gián đoạn tất cả các dòng chảy.

Bước 7.
Xem xét bảo vệ chống xói lở ở hạ lưu của bể. Nếu áp dụng phương án 1 (bước 5), điều kiện dòng chảy rời khỏi bể khớp với điều kiện dòng chảy hạ lưu, và không cần thêm lớp đá hộc (riprap) ở hạ lưu trừ khi có mối quan ngại cụ thể về nhiễu loạn cục bộ. Tuy nhiên, nếu áp dụng phương án 2 (bước 5), thì có khả năng cần riprap cho đến khi dòng chảy chuyển hoàn toàn sang điều kiện hạ lưu. Chương 10 có phần hướng dẫn tính toán riprap cần thiết.

Ví dụ thiết kế: Bể tiêu năng CSU Rigid Boundary (SI)

Thiết kế một bể tiêu năng CSU rigid boundary để chuyển tiếp từ cống RCB sang kênh tự nhiên. Bể này cần làm giảm vận tốc dòng chảy xấp xỉ bằng mực nước hạ lưu.

Cho:

RCB = Cống 2438 x 2438 mm
L = 71.6 m
S = 0.02 m/m
Q = 39.64 m³/s
n = 0.013
y_c = 2.987 m
y_n = 1.829 m

Kênh tự nhiên phía hạ lưu:
W = 12.5 m (bề rộng)
TW = 1.00 m (từ mực nước khống chế hạ lưu)

Giải:

Bước 1. Tính vận tốc \(V_0\), độ sâu \(y_0\) và số Froude Fr tại cửa ra của cống:

• \(y_0 = y_n = 1.829 m\)
• \(V_0 = V_n = 8.87 m/s\)
• \(Fr = \frac{V_0}{\sqrt{g \cdot y_0}} = \frac{8.87}{\sqrt{9.81 \cdot 1.829}} = 2.1\)

Bước 2. Chọn thử một bể từ Bảng 9.1 dựa trên tỷ số mở rộng \(W_B/W_0\) phù hợp với hình học thực tế hoặc các ràng buộc khác. Chọn \(W_B/W_0\), số hàng \(N_r\), số phần tử N, và các tỷ số \(h/y_A\) và L/h.

• Tỷ số bề rộng kênh/cống: 12.5/2.438=5.1
• Thử bể hình chữ nhật như sau:
  • \(W_B/W_0 = 5\)
  • \(W_1/W_0 = 0.63\)
  • \(N_r = 4, N=15\)
  • \(h/y_A = 0.71, L/h=6L/h = 6\)

Bước 3. Xác định điều kiện dòng chảy \(V_A\) và \(y_A\) tại vị trí tiếp cận trường phần tử gồ (cách 2 lần chiều rộng cống về phía hạ lưu):

• \(W_0 = 2(2.438) = 4.876 m\)

Tính \(V_A\) theo Công thức 4.1 hoặc 4.2:

• \(V_A/V_0 = 1.65 – 0.3Fr = 1.65 – 0.3(2.1) = 1.02\)
• \(V_A = 8.87 \cdot 1.02 = 9.047 m/s\)

Với \(4 < W_B/W_0 < 8\), tra \(y_A\) từ Hình 4.3 hoặc 4.4:

• \(y_A/y_0 = 0.33\) với Fr=2.1 và L=2B
• \(y_A = 1.829 \cdot 0.33 = 0.604 m\)

Bước 4. Với tỷ số chiều cao phần tử gồ trên độ sâu \(h/y_A\) và tỷ số chiều dài trên chiều cao L/h, xác định các thông số tiêu tán từ Bảng 9.1:

a. Chiều cao phần tử gồ:
$$h = (h/y_A)y_A = 0.71 \cdot 0.604 = 0.429 m$$

b. Khoảng cách giữa các hàng phần tử:
$$L = (L/h)h = 6 \cdot 0.429 = 2.574 m$$

c. Chiều rộng bể:
$$W_B = (W_B/W_0) \cdot W_0 = 5 \cdot 2.438 = 12.190 m$$

d. Chiều rộng phần tử:
$$W_1 = (W_1/W_0) \cdot W_0 = 0.63 \cdot 2.438 = 1.536 m$$
→ Dùng 1.524 m

e. Góc mở rộng (divergence):
$$\theta = 4/7 + 10L/(7W_0) = 4/7 + 10(2.574)/(7 \cdot 2.438) = 2.07$$
→ Dùng giá trị 2

f. Hệ số cản đáy:
$$C_B = 0.42$$

g. Diện tích cản của phần tử gồ:
$$A_F = W_1 \cdot h = 1.524 \cdot 0.429 = 0.65 m²$$

h. Hệ số \(C_P\):
$$C_P = 0.7 (theo Mục 9.4)$$

i. Tổng chiều dài bể:
$$L_B = 2W_0 + L \cdot N_r = 2(2.438) + 4(2.574) = 15.172 m$$

Bước 5.
Vì chiều rộng của bể \(W_B = 12.190 m\) gần bằng chiều rộng kênh hạ lưu (12.5 m), xác nhận phương án bể thử theo tùy chọn 1. Dùng điều kiện dòng chảy normal \(V_n và y_n\) và giải phương trình 9.1 để tìm \(C_B A_F N\), sau đó so sánh với giá trị \(C_B A_F N\) của bể:

Tính \(C_B A_F N\) từ phương trình 9.1:

• \(y_n\) hạ lưu = 1.001 m
• \(V_B = Q / (W_B y_n) = 39.64 / (12.190 \cdot 1.001) = 39.64 / 12.178 = 3.255 m/s\)

Áp dụng phương trình 9.1:

$$\rho V_0 Q + C_P \cdot \gamma \cdot Y_0^2 W_0 /2 = C_B A_F N \cdot \rho V_A^2 / 2 + \rho V_B Q + \gamma Q^2 / (2 V_B^2 W_B)$$

Các hạng tử với \(V_0\) và \(y_0\): \(1000(8.870)(39.64) + 0.7(9810)(1.829)^2 (2.438)/2 = 379609\)

Các hạng tử với \(V_B\): \(1000(3.255)(39.64) + 9810(39.64)^2 /(2(3.225)^2(12.190)) = 189820\)

Hạng tử với \(C_B A_F N\): \(C_B A_F N \cdot 1000(9.047)^2/2 = 40924 C_B A_F N\)

Từ đó: \((379609 – 189820) = 40924 C_B A_F N \Rightarrow C_B A_F N = 4.63\)

Tính \(C_B A_F N\) cho bể dựa trên các thông số xác định ở bước 2 và 4 (\(N = 15, C_B = 0.42, A_F =\) 0.65 m²). Sử dụng \(C_B A_F N = 0.42 \cdot 0.65 \cdot 15 = 4.12\). Vì 4.12 nhỏ hơn 4.63 (giá trị từ phương trình 9.1), cần thử phương án bể có sức cản lớn hơn (5 hàng phần tử).

Bước 4 (lặp lại lần 2). Với tỷ số \(h/y_A\) và tỷ L/h, xác định lại thông số tiêu tán từ Bảng 9.1: \(W_B/W_0 = 5, N_r = 5, N=19, h/y_A = 0.71, L/h=6,C_B = 0.38\)

a. \(h = 0.71(0.604) = 0.429 m\)
b. \(L = 6(0.429) = 2.574 m\)
c. \(W_B = 5(2.438) = 12.190 m\)
d. \(W_1 = 0.63(2.438) = 1.536 m\) → dùng 1.524 m
e. Góc mở rộng: \(u_e = 4/7 + 10L/(7W_0) = 4/7 + 10(2.574)/(7 \cdot 2.438) = 2.07\) → dùng 2

f. \(C_B = 0.38\)
g. \(A_F = 1.524 \cdot 0.429 = 0.654 m²\)
h. \(C_P = 0.7\)
i. Tổng chiều dài bể: \(L_B = 2W_0 + L \cdot N_r = 2(2.438) + 5(2.574) = 17.746 m\)

Bước 5 (lặp lại lần 2). Tính \(C_B A_F N\) từ phương trình 9.1:

Từ phương trình 9.1: \(C_B A_F N = 4.63\) (vì chiều rộng bể không đổi)

Tính \(C_B A_F N\) cho bể: \(C_B A_F N = 0.38 \cdot 0.654 \cdot 19 = 4.72 > 4.63\)

→ Đáp ứng yêu cầu, OK

Bước 6.
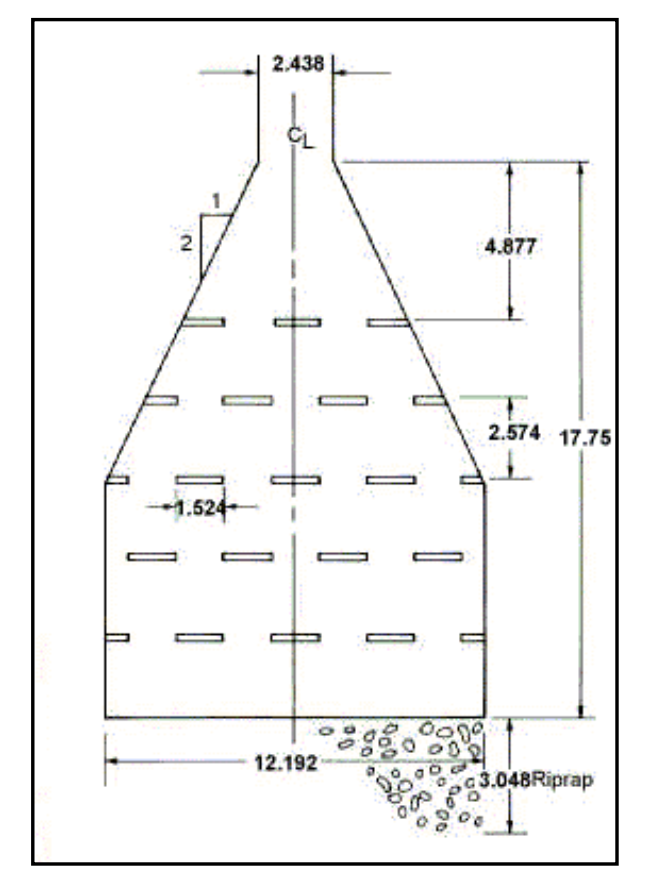
Vẽ sơ đồ bể và bố trí các phần tử thô (xem bản vẽ).
Tất cả kích thước tính bằng mét.

Tỷ lệ \(W_1/h = 1.524 / 0.429 = 3.55\), nằm trong khoảng mục tiêu từ 2 đến 8.

Bước 7.
Vì thiết kế phù hợp với điều kiện hạ lưu, cần tối thiểu lớp đá riprap.
Xem Chương 10 để được hướng dẫn bố trí riprap.

9.2 CONTRA COSTA Basin

Cấu trúc tiêu năng Contra Costa (Keim, 1962) được phát triển tại Đại học California, Berkeley, phối hợp với Hạt Contra Costa, California. Thiết bị này được thiết kế chủ yếu để sử dụng trong các khu vực đô thị có kênh thoát nước hạ lưu rõ ràng. Hình minh họa cấu trúc tiêu năng được thể hiện trong Hình 9.6.

Cấu trúc tiêu năng này được thiết kế để tự làm sạch với yêu cầu bảo trì tối thiểu. Nó phù hợp nhất với các cống nhỏ và trung bình có bất kỳ mặt cắt ngang nào, khi mực nước tại cửa ra nhỏ hơn hoặc bằng một nửa chiều cao cống. Tuy nhiên, nó có thể áp dụng cho nhiều loại kích thước cống và điều kiện vận hành khác nhau như đã nêu ở Bảng 1.1. Dòng chảy rời khỏi cấu trúc tiêu năng sẽ ở trạng thái năng lượng tối thiểu khi không có mực nước hạ lưu. Khi có mực nước hạ lưu, hiệu suất của cấu trúc sẽ được cải thiện.

Kinh nghiệm thực tế với cấu trúc này còn hạn chế. Người thiết kế không nên nội suy các giá trị ngoài phạm vi tham khảo trong hướng dẫn này vượt quá các phạm vi đã được kiểm nghiệm trong mô hình thử nghiệm.

Phương trình 9.6 được xác lập bằng cách thử nghiệm các mô hình tiêu năng Contra Costa có tỷ lệ \(L_2/h_2\) từ 2.5 đến 7. Phương trình này dựa trên vận tốc tại cửa ra của cống \(V_0\), độ sâu \(y_0\), và áp dụng cho cống tròn:

$$\frac{L_2}{h_2} = 1.2 Fr^2 \left( \frac{h_2}{y_0} \right)^{-1.83} \tag{9.6}$$

trong đó:

• \(y_0\) = độ sâu tại cửa ra (m hoặc ft)
• \(V_0\) = vận tốc tại cửa ra (m/s hoặc ft/s)
• \(Fr = \frac{V_0}{\sqrt{g y_0}}\) = số Froude
• \(h_2\) = chiều cao của tấm baffle lớn (m hoặc ft)
• \(L_2\) = chiều dài từ cửa ra đến tấm baffle lớn (m hoặc ft)

Phương trình 9.6 được tổng quát hóa cho các hình dạng khác bằng cách thay độ sâu tương đương của dòng chảy, \(y_e\), thay cho \(y_0\).
Độ sâu tương đương được xác định bằng cách chuyển diện tích dòng chảy tại cửa ra của cống thành tiết diện hình chữ nhật tương đương với bề rộng bằng hai lần độ sâu dòng chảy.
Với cống hộp, \(y_e = y_n\) hoặc \(y_{\text{brink}}\)

$$\frac{L_2}{h_2} = 1.35 Fr^2 \left( \frac{h_2}{y_e} \right)^{-1.83} \tag{9.7a}$$

hoặc:

$$\left( \frac{h_2}{y_e} \right) = \left( \frac{1.35 Fr^2}{L_2/h_2} \right)^{0.546} \tag{9.7b}$$

trong đó:
  \(y_e\) = độ sâu tương đương, \((A/2)^{1/2}\), m (ft)
  A = diện tích dòng chảy tại cửa ra, m² (ft²)
  \(V_0\) = vận tốc tại cửa ra, m/s (ft/s)
  \(Fr = \frac{V_0}{(g \cdot y_e)^{1/2}}\)

Phương trình 9.7b được giải bằng cách giả định một giá trị của \(L_2/h_2\) nằm trong khoảng từ 2.5 đến 7. Từ đó, có thể xác định chiều cao thử nghiệm của tấm baffle thứ hai, \(h_2\). Nếu giá trị khuyến nghị \(L_2/h_2 = 3.5\) được thay vào phương trình 9.7, phương trình thiết kế sẽ trở thành phương trình 9.8. Giá trị \(h_2/y_e\) luôn phải lớn hơn 1.

$$\frac{h_2}{y_e} = 0.595 Fr^{1.092} \tag{9.8}$$

Sau khi xác định được giá trị của \(h_2\) và \(L_2\), chiều dài từ tấm baffle lớn đến đập cuối, \(L_3\), có thể được tính bằng phương trình 9.9:

$$\frac{L_3}{L_2} = 3.75 \left( \frac{h_2}{L_2} \right)^{0.68} \tag{9.9}$$

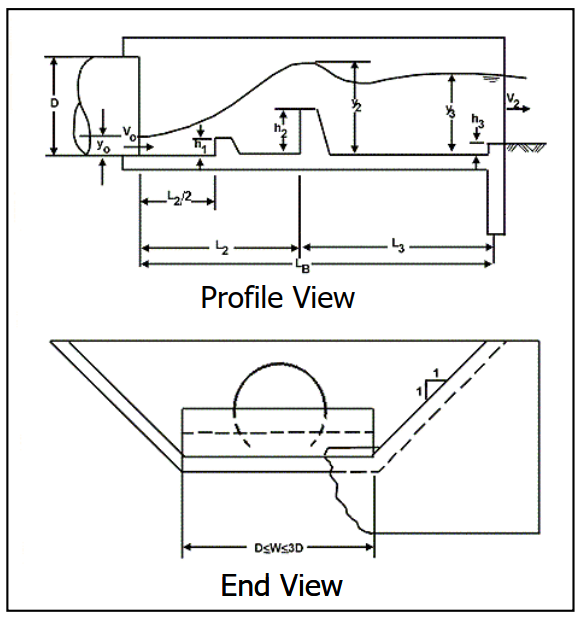
Chiều cao của tấm baffle nhỏ, /(h_1\), bằng một nửa chiều cao của tấm baffle lớn, \(h_2\). Vị trí của tấm baffle nhỏ nằm ở giữa cửa ra của cống và tấm baffle lớn hoặc cách cửa ra một đoạn bằng \(L_2/2\). Độ dốc thành bên của bể thí nghiệm dạng hình thang là 1:1 (V:H). Bề rộng của bể, W, có thể từ một đến ba lần bề rộng của cống. Đáy bể phải gần như nằm ngang. Chiều cao của end still (đập cuối) , h_3, có thể thay đổi từ \(0.062y_2\) đến \(0.10y_2\). Sau khi có được các kích thước bể phù hợp, mực nước mặt tối đa gần đúng, \(y_2\), khi không có mực nước hạ lưu, có thể được xác định theo phương trình 9.10, áp dụng cho bể có tỷ số \(W_B/W_0 = 2\). Độ sâu \(y_3\) bằng với \(y_c\) tại bể cộng với \(h_3\).

$$\frac{y_2}{h_2} = 1.3 \left( \frac{L_2}{h_2} \right)^{0.36} \tag{9.10}$$

Các bước sau đây phác thảo quy trình thiết kế cho cấu tiêu năng Contra Costa:

Bước 1.
Xác định điều kiện dòng chảy tại cửa ra của cống với lưu lượng thiết kế. Nếu độ sâu dòng chảy tại cửa ra, \(y_0\), nhỏ hơn hoặc bằng (D/2, thì có thể áp dụng bể Contra Costa.

Bước 2.
Tính độ sâu tương đương \(y_e\) và số Froude Fr.
  \(y_e = y_0\) đối với cống hình chữ nhật
  \(y_e = (A/2)^{1/2}\) đối với các hình dạng khác
  \(Fr = V_0 / (g y_e)^{1/2}\)

Bước 3.
Chiều rộng đáy bể \(W_B\) được chọn để phù hợp với kênh tự nhiên, nhưng phải nằm trong khoảng từ \(1W_0 đến 3W_0\). Nếu không có kênh tự nhiên xác định, chiều rộng không nên lớn hơn 3 lần bề rộng cống. Độ dốc thành bên của bể nên là 1:1.

Bước 4.
Giả sử một giá trị \(L_2/h_2\) nằm trong khoảng từ 2.5 đến 7. Nếu \(L_2/h_2 = 3.5\), sử dụng Phương trình 9.8 để xác định \(h_2\). Dùng Phương trình 9.7 cho các giá trị khác. Tính \(L_2 = 3.5 \cdot h_2\). Tính chiều cao của tấm baffle thứ nhất, \(h_1 = 0.5 h_2\) và vị trí của nó, \(L_1 = 0.5 L_2\).

Bước 5.
Xác định chiều dài từ tấm baffle lớn đến end still, \(L_3\), sử dụng Phương trình 9.9. Lặp lại quy trình nếu cần thiết cho đến khi xác định được một cấu trúc tiêu năng đáp ứng các yêu cầu thiết kế.

Bước 6.
Ước tính mực nước mặt tối đa gần đúng khi không có mực nước hạ lưu, \(y_2\), sử dụng Phương trình 9.10 trong đó \(W_B = 2W_0\). Đặt chiều cao end still, \(h_3\), trong khoảng từ \(0.06y_2 đến 0.1y_2\). Nếu các kích thước trên phù hợp với địa hình tại hiện trường, thì đó là kích thước cuối cùng. Nếu không, chọn một giá trị \(L_2/h_2\) khác và lặp lại quy trình thiết kế.

Bước 7.
Xác định độ sâu đầu ra của bể \(y_3 = y_c\) và vận tốc đầu ra \(V_2 = V_c\).

$$Q^2/g = (A_c^3)/T_c = [y_c(W_B + y_c)]^3 / (W_B + 2y_c) \quad \text{(thay \(A_c\) và \(T_c\) theo đặc tính hình thang)} Vc=Q/AcV_c = Q / A_c$$

Bước 8.
Có thể cần lát đá riprap ở hạ lưu, đặc biệt với trường hợp không có mực nước hạ lưu. Xem Chương 10 để biết hướng dẫn về bố trí riprap. Freeboard để ngăn tràn và bảo vệ bờ tại phần hạ lưu của bể cũng nên được xem xét.

Ví dụ thiết kế: Bể Contra Costa (SI)

Xác định các kích thước thiết kế cho một bể Contra Costa.

Cho:

• D = 1.219 m (cống RCP đường kính 1.219 m)
• Q = 8.49 m³/s
• \(y_0 = 0.701 m\)
• \(V_0 = 12.192 m/s\)

Chiều rộng đáy kênh = 2.438 m

Giải:

Bước 1.
Xác định điều kiện dòng chảy tại cửa ra của cống với lưu lượng thiết kế.
\(y_0 = 0.701 m\) xấp xỉ D/2, OK.

Bước 2.
Tính độ sâu tương đương \(y_e\) và số Froude .
Dùng Phương trình 7.11 và 7.13, diện tích dòng chảy trong cống = 0.696 m².

$$y_e = (A/2)^{1/2} = (0.696 / 2)^{1/2} = 0.590 \text{ m}$$

$$Fr = \frac{V_0}{(g y_e)^{1/2}} = \frac{12.192}{[9.81 \cdot (0.590)]^{1/2}} = 5.07$$

Bước 3.
Chiều rộng đáy bể \(W_B\) được chọn để phù hợp với kênh tự nhiên. Độ dốc thành bên của bể là 1:1 (V:H).
Chọn W = 2.438 m (chiều rộng đáy kênh). 1≤W/D≤31, OK.

Bước 4.
Giả sử \(L_2/h_2 = 3.5\), dùng Phương trình 9.8 để xác định \(h_2\). Tính \(L_2 = 3.5 h_2\). Tính chiều cao tấm baffle thứ nhất \(h_1 = 0.5 h_2\) và vị trí \(L_1 = 0.5 L_2\).

\(\frac{h_2}{y_e} = 0.595 Fr^{1.092} = 0.595 \cdot (5.07)^{1.092} = 3.5\)

\(h_2 = y_e \cdot (h_2 / y_e) = 0.590 \cdot (3.50) = 2.065 \text{ m} \)

\(L_2 = 3.5 \cdot h_2 = 3.5 \cdot (2.065) = 7.228 \text{ m} \)

\(h_1 = 0.5 h_2 = 0.5 \cdot (2.065) = 1.032 \text{ m} \)

\(L_1 = 0.5 L_2 = 0.5 \cdot (7.228) = 3.614 \text{ m} \)

Bước 5.
Xác định chiều dài từ tấm baffle lớn đến end still \(L_3\) bằng Phương trình 9.9.
Lặp lại nếu cần để tối ưu thiết kế.

\(\frac{L_3}{L_2} = 3.75 \left( \frac{h_2}{L_2} \right)^{0.68} = 3.75 (2.065 / 7.228)^{0.68} = 1.6 \)

\(L_3 = \left( \frac{L_3}{L_2} \right) \cdot L_2 = 1.6 \cdot (7.228) = 11.56 \text{ m}\)

Bước 6.
Ước tính mực nước mặt tối đa gần đúng khi không có mực nước hạ lưu \(y_2\), dùng Phương trình 9.10 với \(W_B = 2D\).
Xác định chiều cao end still \(h_3 = 0.1 y_2\)

\(\frac{y_2}{h_2} = 1.3 \left( \frac{L_2}{h_2} \right)^{0.36} = 1.3 (3.5)^{0.36} = 2.04\)

\(y_2 = \left( \frac{y_2}{h_2} \right) \cdot h_2 = 2.04 \cdot 2.065 = 4.21 \text{ m}\)

\(h_3 = 0.1 y_2 = 0.1 \cdot (4.21) = 0.42 \text{ m}\)

Tóm tắt các kích thước vật lý được thể hiện trong bảng sau.

	First Baffle	Second Baffle	End Sill
Distance from exit (m)	3.61	7.23	18.79
Height (m)	1.03	2.07	0.42

Bước 7.
Xác định độ sâu tại cửa ra của bể \(y_3 = y_c\) và vận tốc đầu ra \(V_2 = V_c\).

\({Q^2}{g T_c} = \frac{(A_c)^3}{T_c} = \frac{[y_c(W_B + y_c)]^3}{W_B + 2y_c}\)

\(\frac{8.49^2}{9.81} = 7.35 = \frac{[y_c(2.438 + y_c)]^3}{2.438 + 2y_c}\)

Bằng phương pháp thử và sai, \(y_c = 0.938 m, T_c = 4.314 m, A_c = 3.17 m² \)

\(V_c = \frac{Q}{A_c} = \frac{8.49}{3.17} = 2.68 \text{ m/s}\)

Bước 8.
Có thể cần lát đá riprap ở hạ lưu, đặc biệt trong trường hợp không có mực nước hạ lưu. Xem Chương 10 để biết các khuyến nghị thiết kế.
Cần xem xét khoảng không chống tràn (freeboard) để ngăn dòng nước tràn và một tường chắn chân để tránh xói lở bên dưới đáy bể.

9.3 HOOK Basin

Hook basin được phát triển tại Đại học California phối hợp với Cục Đường cao tốc California và Cục Đường công cộng (MacDonald, 1967). Bể này ban đầu được thiết kế cho các cống vòm lớn với mực nước hạ lưu thấp, nhưng cũng có thể sử dụng cho cống hộp hoặc cống tròn. Thiết bị tiêu năng này có thể được sử dụng cho các cửa ra cống với số Froude từ 1.8 đến 3.0.

Hai nghiên cứu mô hình thủy lực đã được thực hiện:
(1) một bể với tường cánh cong từ phương thẳng đứng tại cửa ra cống chuyển dần về độ dốc thành 1:1.5 (V:H) tại end still (đập cuối) và đáy bể thu hẹp dần được trình bày trong Mục 9.3.1
(2) một kênh hình thang có tiết diện đều được trình bày trong Mục 9.3.2

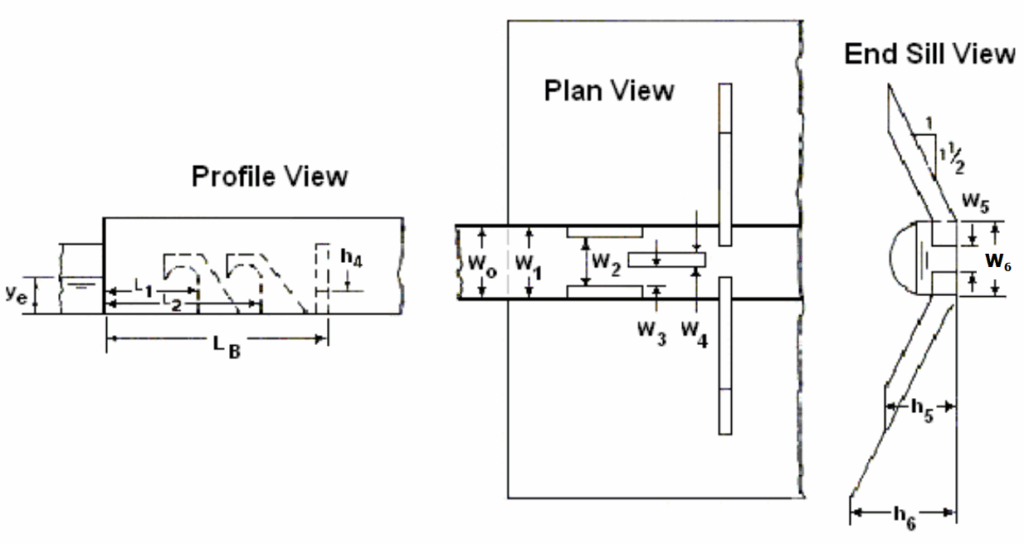
9.3.1 Hook Basin with Warped Wingwalls

Hook basin với tường cánh warped được minh họa trong Hình 9.7. Quy trình thiết kế là xác định được ngoại trừ việc lựa chọn chiều rộng của phần hook. Cần sử dụng phán đoán kỹ thuật để chọn chiều rộng sao cho đủ lớn để tiêu tán năng lượng hiệu quả, nhưng không quá lớn đến mức dòng chảy giữa các hook không đủ. Tỷ số \(W_4/W_0 = 0.16\), là giá trị nhỏ nhất đã thử nghiệm, được khuyến nghị. Mỗi thiết kế cần được kiểm tra để đảm bảo rằng khoảng cách giữa các hook nằm trong khoảng từ 1.5 đến 2.5 lần chiều rộng hook.

Chiều cao của tường cánh, \(h_6\), nên bằng ít nhất hai lần độ sâu dòng chảy tại cửa ra cống hoặc \(2y_e\). Chiều cao này dựa trên mực nước mặt cao nhất quan sát được trong bể trong quá trình nghiên cứu. Vì vậy, chọn \(h_6 = 2y_e\) không cung cấp khoảng an toàn (freeboard) để chứa nước bắn tung. Tùy thuộc vào điều kiện thực địa, người thiết kế nên dự phòng thêm khoảng an toàn chống tràn.

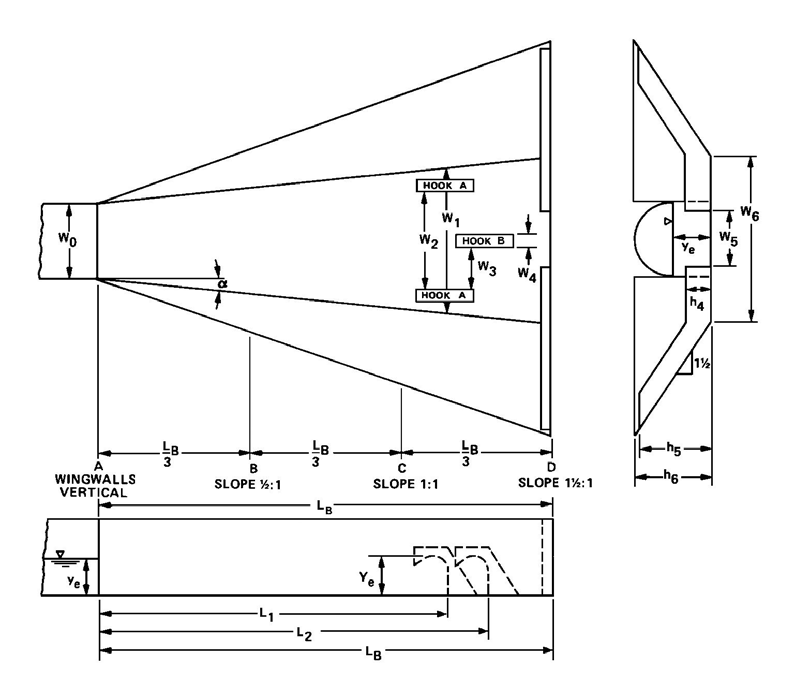
(nd: Warped Wingwall)

Warpped wingwalls là tường cánh được uốn dần từ dạng thẳng đứng tại cửa ra cống sang độ dốc nghiêng tại phần cuối của bể (ví dụ: nghiêng 1:1.5).

Mục đích là để hướng dòng chảy và giảm sốc thủy lực, giúp tiêu năng hiệu quả hơn.

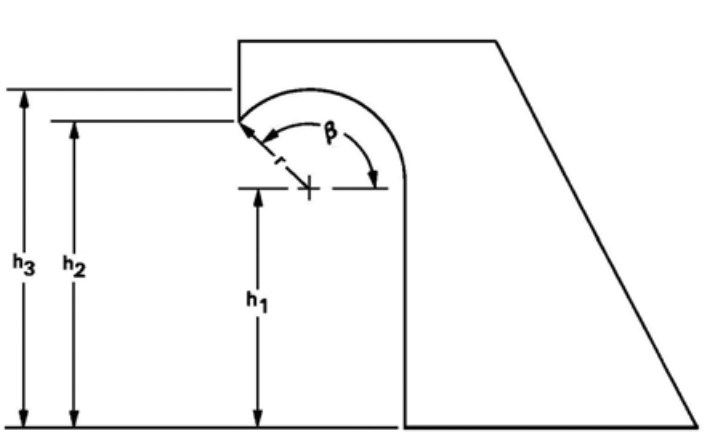
Phạm vi kích thước thiết kế tốt nhất đã được kiểm nghiệm được nêu trong quy trình thiết kế. Trong hầu hết các trường hợp, tỷ lệ cho ra kích thước nhỏ nhất đã được sử dụng. Cấu hình hook được khuyến nghị được thể hiện trong Hình 9.8. Các kích thước khuyến nghị là:

1. \(h_3 = y_e\)
2. \(h_2 = 1.28 h_1\)
3. \(h_1 = y_e / 1.4\)
4. \(\beta = 135^\circ\)
5. \(r = 0.4 h_1\)

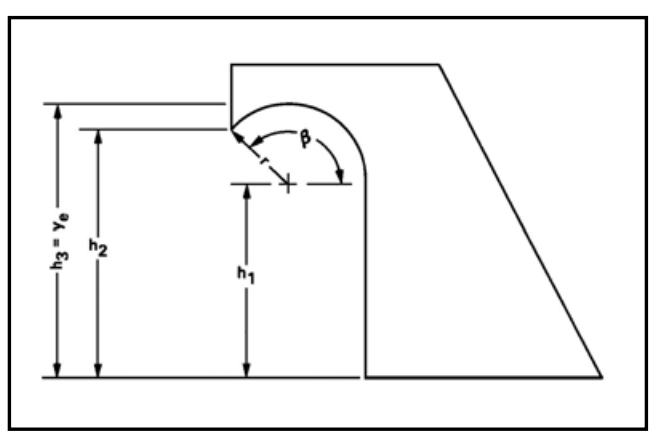
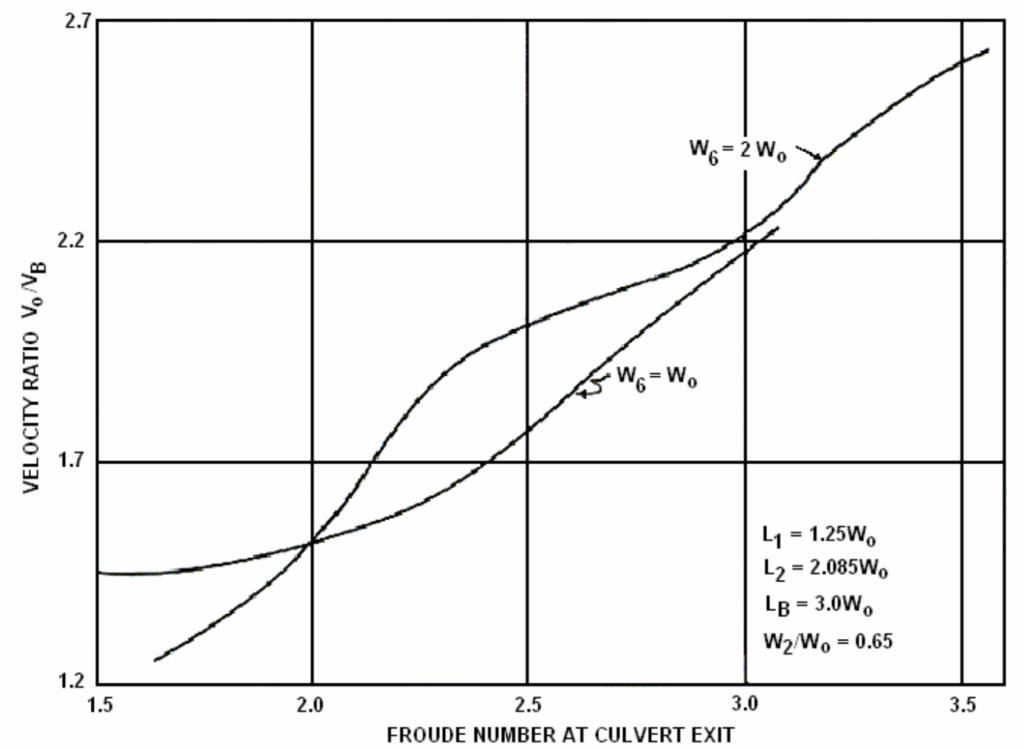
Một góc mở rộng (flare angle), α, là 5.7 độ mỗi bên (với tan⁡α=0.10) là giá trị tối ưu khi Fr > 2.45. Tăng chiều dài bể vượt quá \(L_B = 3W_0\) sẽ không cải thiện hiệu suất của bể.
Hiệu quả của cấu trúc này giảm nhanh khi số Froude tăng, bất kể chiều rộng của hook, nếu góc mở rộng vượt quá 5.7 độ.

Vận tốc tại cửa ra của cấu trúc, \(V_B\), được ước lượng từ Hình 9.9.
Tỷ số vận tốc càng cao, \(V_0 / V_B\), thì tiêu năng càng hiệu quả trong việc tiêu tán năng lượng và phân phối dòng chảy về hạ lưu.

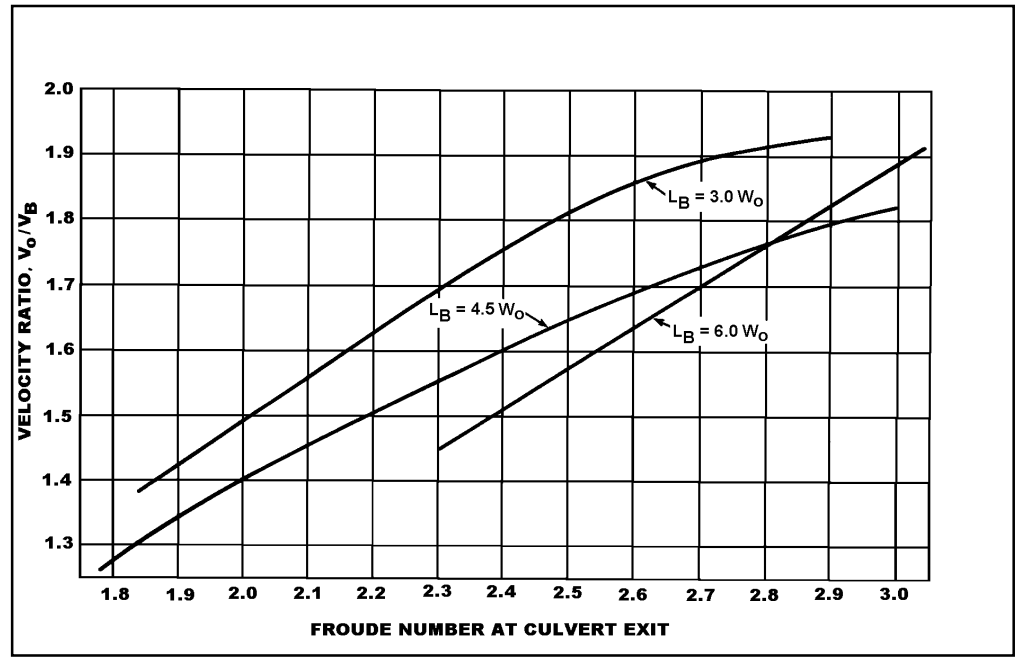
Tùy thuộc vào vận tốc cuối cùng và điều kiện đất, có thể xảy ra hiện tượng xói lở ở hạ lưu của bể.
Người thiết kế nếu cần thiết, cần bố trí lớp bảo vệ riprap tại khu vực này. Chương 10 cung cấp hướng dẫn thiết kế riprap.
Nếu dự đoán có mảnh vụn lớn (debris), nên bọc thép mặt hướng thượng lưu của hook để bảo vệ.

Quy trình thiết kế được khuyến nghị cho Hook basin với Warped Wingwall (tường cánh uốn) như sau:

Bước 1.
Tính vận tốc tại cửa ra cống \(V_0\), độ sâu tương đương \(y_e\), và số Froude \(Fr = \frac{V_0}{(g y_e)^{1/2}}\)

Nếu 1.8<Fr<3.0, tiếp tục thiết kế.

Bước 2.
Tính vận tốc kênh hạ lưu \(V_n\) và độ sâu \(y_n\).

Bước 3.
Chọn chiều rộng của bể tại cửa ra \(W_B\) (hay \(W_6\)), và tính \(L_B\).
Nếu có kênh hạ lưu, \(W_6\) nên xấp xỉ bằng chiều rộng kênh.

\(L_B = \frac{W_6 – W_0}{2 \tan \alpha}, \quad \text{dùng } \alpha = 5.7^\circ \text{ (} \tan \alpha = 0.10 \text{)}\)

Bước 4.
Tính vị trí và khoảng cách các hook (xem Hình 9.7):

a. Khoảng cách đến hàng hook đầu tiên:

\(L_1 = 0.75 L_B \quad (\text{phạm vi cho phép: } 0.75 < L_1/L_B < 0.80)\)

b. Chiều rộng tại hàng hook đầu tiên:

\(W_1 = 2L_1 (\tan \alpha) + W_0\)

c. Khoảng cách giữa các hook trong hàng A:

\(W_2 = 0.66 W_1 \quad (\text{phạm vi cho phép: } 0.66 < W_2/W_1 < 0.70)\)

d. Khoảng cách đến hàng hook thứ hai (hàng B):

\(L_2 = 0.83 L_B \quad (\text{phạm vi cho phép: } 0.83 < L_2/L_B < 0.89)\)

e. Chiều rộng của các hook:

\(W_4 = 0.16 W_0\)

f. Khoảng cách ngang giữa hook hàng A và B:

\(W_3 = \frac{W_2 – W_4}{2}\)

Nếu không thỏa mãn \(1.5 < W_3/W_4 < 2.5\), điều chỉnh \(W_4\) cho phù hợp.

Bước 5.
Tính các kích thước của hook (xem Hình 9.8):

a. Chiều cao đến tâm bán kính:
  \(h_1 = y_e / 1.4\)

b. Chiều cao đến đỉnh:
  \(h_2 = 1.28 h_1\)

c. Chiều cao đến đỉnh bán kính:
  \(h_3 = y_e\)

d. Góc bán kính:
  \(\beta = 135^\circ\)

e. Bán kính:
  \(r = 0.4 h_1\)

Bước 6.
Tính kích thước của end still (đập cuối) và tường cánh (xem Hình 9.7):

a. Chiều cao end stilli:
  \(h_4 = 0.67 y_e\)

b. Chiều rộng khe mở trên end still:
  \(W_5 = 0.33 W_6\)

c. Chiều cao đến đỉnh tường cánh :
  \(h_6 = 2 y_e \) (tối thiểu)

d. Chiều cao đến đỉnh end still:
  \(h_5 = 0.94 h_6\)

Bước 7.
Tìm tỷ số \(V_0 / V_B\) từ Hình 9.9 và tính vận tốc tại cửa ra của bể \(V_B\). So sánh \(V_B\) với \(V_n\) từ bước 2. Nếu \(V_B\) không chấp nhận được, điều chỉnh chiều dài bể.
Đánh giá khả năng xói ở hạ lưu dựa trên điều kiện đất và vận tốc đầu ra. Nếu cần riprap, xem Chương 10.

Bước 8.
Khi dự đoán có mảnh vụn lớn, mặt thượng lưu của các hook nên được bọc thép.

Ví dụ thiết kế: Hook Basin với Warped Wingwalls (SI)

Xác định các kích thước cho một Hook basin (xem Hình 9.7) cho một cống vòm bán nguyệt bằng bê tông dài có kích thước 3.658 m chiều rộng và 3.658 m từ đáy đến đỉnh vòm.

Cho:

• \(S_0 = 0.020 m/m\)
• n = 0.012
• Q = 76.41 m³/s
• \(y_e\) = 1.829 m
• \(V_0 = 11.43 m/s\)

Kênh hạ lưu có dạng hình thang với các đặc tính sau:

• \(W_c = 6.096 m\)
• \(S_0 = 0.020 m/m\)
• Z=1.5
• n = 0.030
• \(V_n = 5.27 m/s\)
• \(y_n = 1.676 m\)

Giải :

Bước 1.
Tính vận tốc tại cửa ra cống \(V_0\), độ sâu tương đương \(y_e\), và số Froude Fr, \(V_0 / \sqrt{g y_e}\).
Đã cho \(V_0 = 11.43 m/s\) và \(y_e = 1.829 m\). \(Fr_0 = \frac{11.43}{\sqrt{9.81 \cdot 1.829}} = 2.70\)

Vì 1.8 < 2.70 < 3, tiếp tục sang bước 2.

Bước 2.
Tính vận tốc và độ sâu dòng chảy hạ lưu \(V_n = 5.27 m/s\) và \(y_n = 1.676 m\) (đã cho).

Bước 3.
Chọn \(W_6\) và tính \(L_B\).
Dùng \(W_6 = W_c = 6.096 m\) và tan⁡α=0.10

\(L_B = \frac{W_6 – W_0}{2 \tan \alpha} = \frac{6.096 – 3.658}{2 \cdot 0.10} = 12.19 \text{ m (hay } 3.3 W_0\text{)}\)

Bước 4.
Tính vị trí và khoảng cách các hook (xem Hình 9.7):

a. Khoảng cách đến hàng hook đầu tiên:

\(L_1 = 0.75 L_B = 0.75 \cdot 12.19 = 9.143 \text{ m}\)

b. Chiều rộng tại vị trí hook đầu tiên:

\(W_1 = 2L_1 \tan \alpha + W_0 = 2(9.143)(0.1) + 3.658 = 5.487 \text{ m}\)

c. Khoảng cách giữa các hook hàng A:

\(W_2 = 0.66 W_1 = 0.66 \cdot 5.487 = 3.621 \text{ m}\)

d. Khoảng cách đến hàng hook thứ hai (hàng B):

\(L_2 = 0.83 L_B = 0.83 \cdot 12.19 = 10.118 \text{ m}\)

e. Chiều rộng các hook:

\(W_4 = 0.16 W_0 = 0.16 \cdot 3.658 = 0.585 \text{ m}\)

f. Khoảng cách ngang giữa hook A và B:

\(W_3 = \frac{W_2 – W_4}{2} = \frac{3.621 – 0.585}{2} = 1.518 \text{ m}\)

\(\frac{W_3}{W_4} = \frac{1.518}{0.585} = 2.6 \text{ (không thỏa mãn } 1.5 < \frac{W_3}{W_4} < 2.5\text{)}\)

Điều chỉnh: \(W_4 = \frac{W_3}{2.5} = \frac{1.518}{2.5} = 0.607 \text{ m}\)

Bước 5.
Tính kích thước hook (xem Hình 9.8):

a. Chiều cao đến tâm bán kính: \(h_1 = y_e / 1.4 = 1.829 / 1.4 = 1.306 \text{ m}\)

b. Chiều cao đến đỉnh: \(h_2 = 1.28 h_1 = 1.28 \cdot 1.306 = 1.672 \text{ m}\)

c. Chiều cao đến đỉnh bán kính: \(h_3 = y_e = 1.829 \text{ m}\)

d. Góc: \(\beta = 135^\circ\)

e. Bán kính: \(r = 0.4 h_1 = 0.4 \cdot 1.306 = 0.522 \text{ m}\)

Bước 6.
Tính kích thước end still và tường cánh (xem Hình 9.7):

a. Chiều cao end still: \(h_4 = 0.67 y_e = 0.67 \cdot 1.829 = 1.225 \text{ m}\)

b. Chiều rộng khe mở trong end still: \(W_5 = 0.33 W_6 = 0.33 \cdot 6.096 = 2.012 \text{ m}\)

c. Chiều cao đến đỉnh tường cánh: \(h_6 = 2 y_e = 2 \cdot 1.829 = 3.658 \text{ m}\)

d. Chiều cao đến đỉnh end still: \(h_5 = 0.94 h_6 = 0.94 \cdot (2 y_e) = 0.94 \cdot 3.658 = 3.439 \text{ m}\)

Bước 7.
Tìm \(V_0 / V_B\) từ Hình 9.9 và tính \(V_B\). So sánh với \(V_n\) ở Bước 2. Đánh giá khả năng xói ở hạ lưu dựa trên điều kiện đất và vận tốc đầu ra. Nếu cần riprap, xem Chương 10.

Với FFr = 2.7 và \(L_B = 3.3 W_0\), thì \(V_0 / V_B < 1.9\)

\(V_B = \frac{11.43}{1.9} \approx 6.016 \text{ m/s}\)

Vận tốc này cao hơn một chút so với vận tốc kênh hạ lưu, cho thấy có thể cần riprap để bảo vệ. Xem Chương 10.

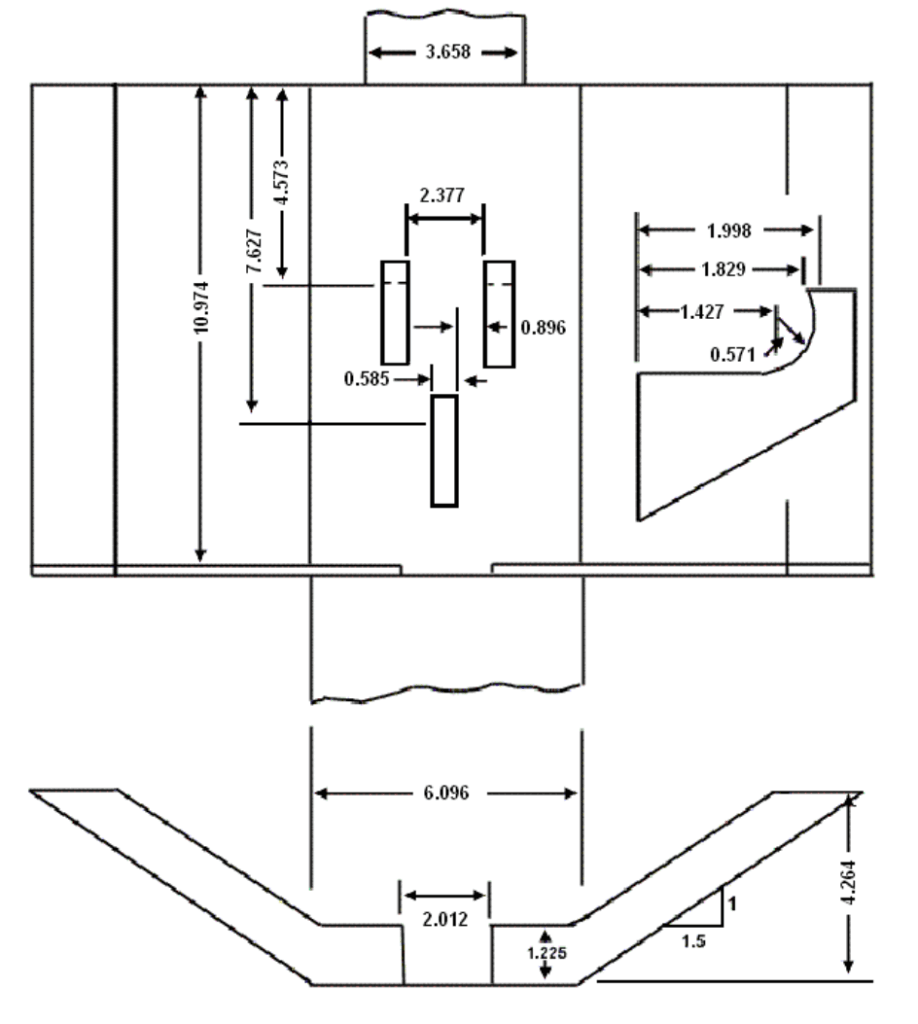
Bản vẽ thiết kế thiết bị tiêu năng được thể hiện bên dưới. (Tất cả kích thước tính bằng mét.)

Bước 8.
Vì không có mảnh vụn lớn được dự đoán tại vị trí này, nên mặt trước của hook sẽ không được bọc thép.

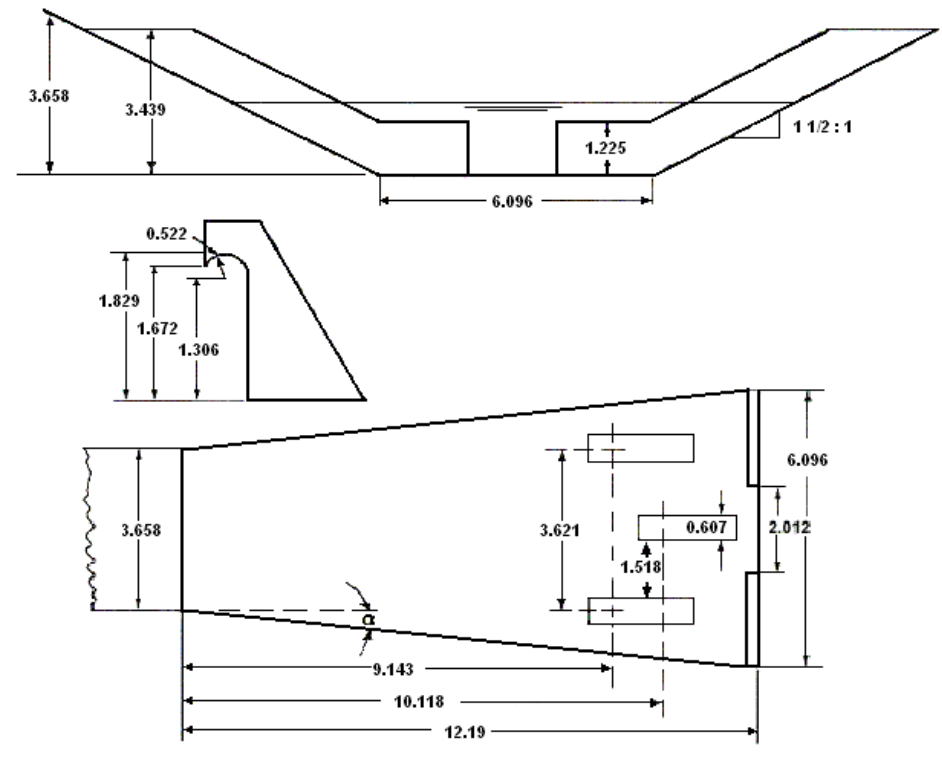
9.3.2 Hook Basin with Uniform Trapezoidal Channel

Hook basin với kênh hình thang đều và end sill được minh họa trong Hình 9.10. Các hook và end sill nằm gần cửa ra của cống hơn so với hook và end sill trong cấu hình có warped wingwalls.

Báo cáo nghiên cứu (MacDonald, 1967) trình bày nhiều biểu đồ cho thấy ảnh hưởng của các biến số khác nhau đến hiệu suất của cấu trúc này. Các biểu đồ này chỉ ra rằng, với một điều kiện lưu lượng xác định, việc mở rộng bể sẽ làm giảm phần nào vận tốc ở hạ lưu, và việc làm phẳng độ dốc thành bên sẽ cải thiện hiệu suất của cấu trúc với số Froude lên đến 3.0.

Phạm vi tốt nhất của các kích thước thiết kế đã được kiểm nghiệm và thể hiện trong quy trình thiết kế. Trong hầu hết các trường hợp, tỷ lệ tạo ra kích thước nhỏ nhất được sử dụng.
Cấu hình hook được khuyến nghị thể hiện trong Hình 9.11.
Các kích thước chiều cao khác với loại sử dụng warped wingwalls. Các kích thước khuyến nghị là:

1. \(h_2\) = y_e
2. \(h_3 = 1.4 h_1\)
3. \(\beta = 135^\circ\)
4. \(r = 0.4 h_1\)

Vận tốc dòng chảy tại cửa ra của cấu trúc này, \(V_B\), được ước lượng từ Hình 9.12.

Quy trình thiết kế cho Hook basin với kênh hình thang đều được thực hiện như sau:

Bước 1.
Tính vận tốc tại cửa ra của cống \(V_0\), độ sâu tương đương \(y_e = \sqrt{A/2}\), và số Froude: \(Fr = \frac{V_0}{\sqrt{g y_e}}\)

Chiều rộng \(W_0\) = bề rộng của cống chữ nhật, hoặc \(W_0 = 2 y_e\) đối với cống tròn và các dạng khác.

Nếu 1.8 < Fr < 3.0, tiếp tục thiết kế.

Bước 2.
Tính vận tốc dòng chảy và độ sâu kênh hạ lưu: \(V_n, y_n\)

Bước 3.
Chọn chiều rộng bể \(W_B\) (với \(W_6 = W_B\)), độ dốc thành bên và chiều dài bể L_B.

\(W_6\) nên xấp xỉ bằng chiều rộng kênh nếu đã xác định kênh hạ lưu. \(W_6 = W_0 \text{ đến } 2 W_0\)

Độ dốc thành bên bể có thể từ 1:1.5 đến 1:2 (V:H) \(L_B = 3.0 W_0\)

Bước 4.
Tính vị trí và khoảng cách các hook (xem Hình 9.10):

a. Khoảng cách đến hook hàng đầu tiên:
  \(L_1 = 1.25 W_0\(

b. Chiều rộng tại hook đầu tiên:
  \(W_1 = W_0\)

c. Khoảng cách giữa các hook hàng đầu tiên:
  \(W_2 = 0.65 W_0\)

d. Khoảng cách đến hook hàng thứ hai:
  \(L_2 = 2.085 W_0\)

e. Chiều rộng hook:
  \(W_4 = 0.16 W_0\)

f. Khoảng cách giữa hook hàng A và B:
  \(W_3 = \frac{W_2 – W_4}{2}\)
  Nếu không thỏa mãn \(W_3 / W_4 \geq 1.0\), điều chỉnh \(W_6\)

Bước 5.
Tính kích thước hook (xem Hình 9.11):

a. Chiều cao đến tâm bán kính:
  \(h_1 = 0.78 y_e\)

b. Chiều cao đến đỉnh hook:
  \(h_2 = y_e\)

c. Chiều cao đến đỉnh bán kính:
  \(h_3 = 1.4 h_1\)

d. Góc của bán kính cong:
  \(\beta = 135^\circ\)

e. Bán kính cong:
  \(r = 0.4 h_1\)

Bước 6.
Tính kích thước end sill và tường cánh (xem Hình 9.10):

a. Chiều cao end sill:
  \(h_4 = 0.67 y_e\)

b. Chiều rộng khe mở trong end sill:
  \(W_5 = 0.33 W_B\)

c. Chiều cao đến đỉnh thành bên:
  \(h_6 = 3.33 y_e\) với dốc 1:1.5
  \(h_6 = 2.69 y_e\) với dốc 1:2

d. Chiều cao đến đỉnh end sill:
  \(h_5 = 0.70 h_6\)

Bước 7.
Tìm \(V_0 / V_B\) từ Hình 9.12 và tính \(V_B\). So sánh với \(V_n\) từ bước 2.
Nếu \(V_B\) không chấp nhận được, điều chỉnh \(W_6\) nếu có thể. Đánh giá khả năng xói ở hạ lưu dựa trên điều kiện đất và vận tốc đầu ra. Nếu cần riprap, xem Chương 10.

Bước 8.
Nếu có mảnh vụn lớn, mặt thượng lưu của hook nên được bọc thép.

Ví dụ thiết kế: Hook Basin với Kênh Hình Thang Đều (SI)

Xác định các kích thước cho một Hook basin với kênh hình thang đều cho một cống vòm bán nguyệt bê tông dài có kích thước 3.658 m chiều rộng và 3.658 m từ đáy đến đỉnh vòm.

Cho:

• \(S_0 = 0.020 m/m\)
• n = 0.012
• Q = 76.41 m³/s
• \(y_e = 1.829 m\)
• \(V_0 = 11.43 m/s\)

Kênh hạ lưu có dạng hình thang với các đặc tính sau:

• \(W_c = 6.096 m\)
• \(S_0 = 0.020 m/m\)
• Z = 1.5
• n = 0.030
• \(V_n = 5.27 m/s\)
• \(y_n = 1.676 m\)

Giải:

Bước 1.
Tính vận tốc tại cửa ra cống \(V_0\), độ sâu tương đương \(y_e\), và số Froude

\(Fr = \frac{V_0}{\sqrt{g y_e}} = \frac{11.43}{\sqrt{9.81 \cdot 1.829}} = 2.70\)

Vì 1.8 < 2.70 < 3, tiếp tục sang bước 2.

Bước 2.
Tính vận tốc và độ sâu của kênh hạ lưu:
Đã cho: \(V_n = 5.273 m/s\) và\(y_n = 1.676 m\)

Bước 3. Chọn chiều rộng bể, \(W_6\), độ dốc thành bên, và chiều dài, \(L_B\). \(W_6\) nên xấp xỉ bằng chiều rộng kênh nếu kênh hạ lưu đã được xác định.

\(W_6 = W_c = 6.096 \text{ m}, \text{ tức là } \frac{6.096}{3.658} = 1.67 \, W_0\)

Độ dốc thành bên của bể sẽ là 1:1.5 (V:H)

\(L_B = 3.0 W_0 = 3.0(3.658) = 10.974 \text{ m}\)

Bước 4. Tính vị trí và khoảng cách các hook (xem Hình 9.10):

a. khoảng cách đến hook đầu tiên, \(L_1 = 1.25 \, W_0 = 1.25(3.658) = 4.573 m\)

b. chiều rộng tại hook đầu tiên, \(W_1 = W_0 = 3.658 m\)

c. khoảng cách giữa các hook đầu tiên, \(W_2 = 0.65 \, W_0 = 0.65(3.658) = 2.377 m\)

d. khoảng cách đến hook thứ hai, \(L_2 = 2.085 \, W_0 = 2.085(3.658) = 7.627 m\)

e. chiều rộng của hook, \(W_4 = 0.16 \, W_0 = 0.16(3.658) = 0.585 m\)

f. khoảng cách giữa hook hàng đầu tiên và hàng thứ hai, \(W_3\)

\(W_3 = \frac{W_2 – W_4}{2} = \frac{2.377 – 0.585}{2} = 0.896 \text{ m}\)

\(\frac{W_3}{W_4} = \frac{0.896}{0.585} = 1.5, \text{ thỏa mãn điều kiện } W_3/W_4 \geq 1.0\)

Bước 5. Tính các kích thước hook (xem Hình 9.11):

a. chiều cao đến tâm bán kính, \(h_1 = 0.78 y_e = 0.78(1.829) = 1.427 m\)

b. chiều cao đến đỉnh, \(h_2 = y_e = 1.829 m\)

c. chiều cao đến đỉnh bán kính, \(h_3 = 1.4 h_1 = 1.4(1.427) = 1.998 m\)

d. góc bán kính, \(\beta = 135^\circ\)

e. bán kính, \(r = 0.4 h_1 = 0.4(1.427) = 0.571 m\)

Bước 6. Tính kích thước end sill và tường chắn (xem Hình 9.10):

a. chiều cao end sill, \(h_4 = 0.67 y_e = 0.67(1.829) = 1.225 m\)

b. chiều rộng khe mở trên end sill, \(W_5 = 0.33 W_B = 0.33(6.096) = 2.012 m\)

c. chiều cao đến đỉnh mái taluy, với dốc 1:1.5 (V:H): \(h_6 = 3.33 y_e = 3.33(1.829) = 6.091 m\)

d. chiều cao đến đỉnh end sill, /(h_5 = 0.70 h_6 = 0.70(6.091) = 4.264 m/)

Bước 7. Tìm \(V_0 / V_B\) từ Hình 9.12 và tính \(V_B\). So sánh với \(V_n\) từ bước 2.

Đánh giá nguy cơ xói lở ở hạ lưu dựa trên điều kiện đất và vận tốc dòng chảy. Nếu cần riprap, xem Chương 10.

Từ Hình 9.12 với số Froude bằng 2.70 và \(W_6/W_0 = 1.67\), thì: \(V_0 / V_B \approx 2.0 \Rightarrow V_B = \frac{11.43}{2} = 5.72 \, \text{m/s}\)

Giá trị này hơi lớn hơn vận tốc trong kênh hạ lưu Vn=5.273V_n = 5.273 m/s → có thể cần riprap tối thiểu.

Bước 8. Nếu có mảnh vụn lớn, mặt thượng lưu của hook nên được bọc thép.
Vì không có mảnh vụn lớn được dự đoán, mặt hook sẽ không được bọc thép.

Các kích thước ví dụ thiết kế cho cả hai loại bể warped wingwall và trapezoidal được trình bày trong bảng sau.

Bảng kích thước ví dụ thiết kế cho Hook Basin

Hạng mục	Thành phần	Ký hiệu	Warped Wingwall (m)	Trapezoidal (m)
Basin	Chiều dài	\(L_B\)	12.19	10.974
	Chiều rộng	\(W_6\)	6.096	6.096
First Hooks	Khoảng cách	\(L_1\)	9.143	4.573
	Khoảng cách giữa	\(W_2\)	3.621	2.377
Second Hook	Khoảng cách	\(L_2\)	10.118	7.682
	Khoảng cách giữa	\(W_3\)	1.518	0.896
End Wall	Chiều cao	\(h_4\)	1.225	1.225
	Khe mở (Slot)	\(W_5\)	2.012	2.012
	Đỉnh	\(h_5\)	3.439	4.264
Hooks	Chiều cao	\(h_3\)	1.829	1.998
	Chiều rộng	\(W_4\)	0.607	0.585

9.4 USBR TYPE VI Impact Basin

Bể tiêu năng loại VI của USBR (USBR Type VI Impact Basin) được phát triển tại Phòng Thí nghiệm của Cục Khai hoang Hoa Kỳ (USBR), theo ASCE (1957). Thiết bị tiêu năng này nằm trong một cấu trúc dạng hộp khá nhỏ gọn, và yêu cầu có mực nước hạ lưu (tailwater) để hoạt động hiệu quả. Mặc dù tài liệu này nhấn mạnh việc sử dụng tại cửa ra của cống, cấu trúc cũng có thể được sử dụng cho các kênh hở.

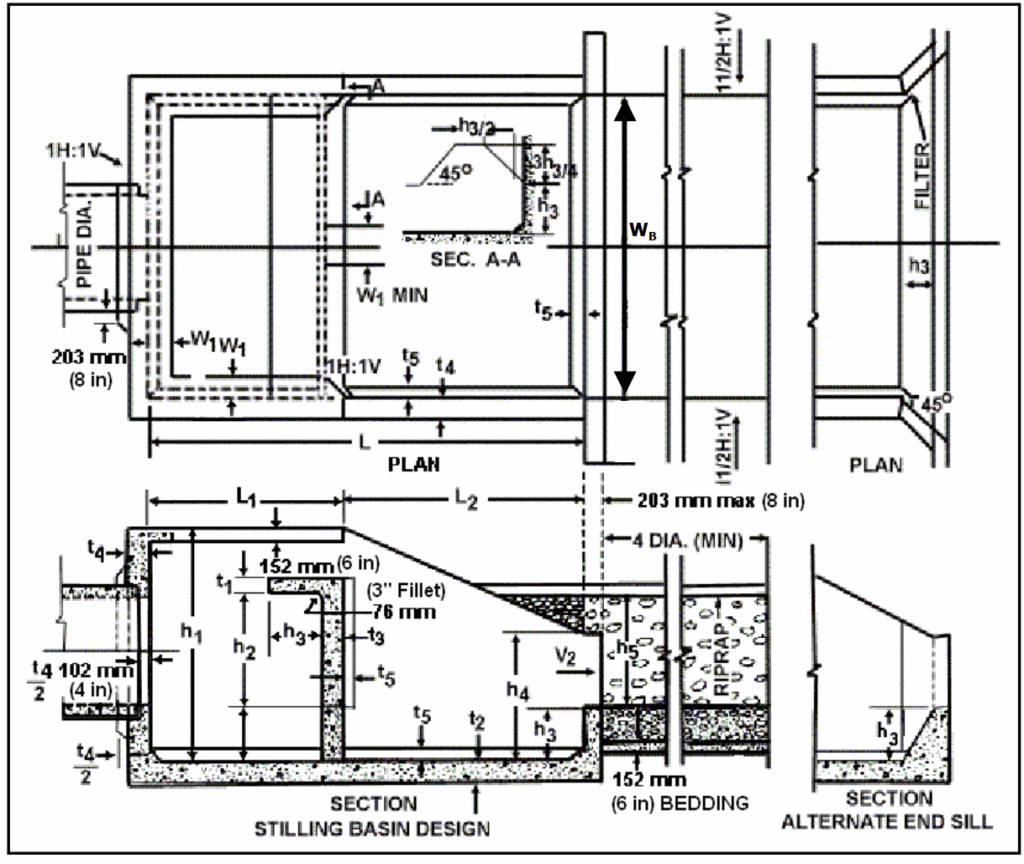
Hình dạng của bể đã được phát triển qua nhiều thử nghiệm, tuy nhiên bị giới hạn trong phạm vi thực tế yêu cầu ở hiện trường. Với nhiều kết hợp của lưu lượng, vận tốc, và độ sâu dòng chảy đầu vào, nhu cầu rõ ràng là cần một cấu trúc có thể hiệu quả trong toàn bộ phạm vi. Tấm chắn đứng treo (vertical hanging baffle) thể hiện trong Hình 9.13 là thiết bị được chọn. Quá trình tiêu năng xảy ra khi dòng chảy đập vào tấm chắn treo thẳng đứng, bị phản hướng ngược lại bởi phần ngang của tấm chắn và bởi đáy bể, tạo ra các xoáy ngang.

Các rãnh (notch) được bố trí trên tấm chắn để hỗ trợ làm sạch bể sau các khoảng thời gian lưu lượng thấp hoặc không có dòng chảy. Nếu bể bị lắng đầy trầm tích, các rãnh này sẽ tạo ra tia nước tập trung giúp xối sạch. Bể được thiết kế để dòng chảy có thể tràn hoàn toàn qua đỉnh tấm chắn nếu không gian phía dưới bị nghẽn hoàn toàn. Mặc dù đây không phải là chế độ vận hành lý tưởng, nó vẫn chấp nhận được trong thời gian ngắn.

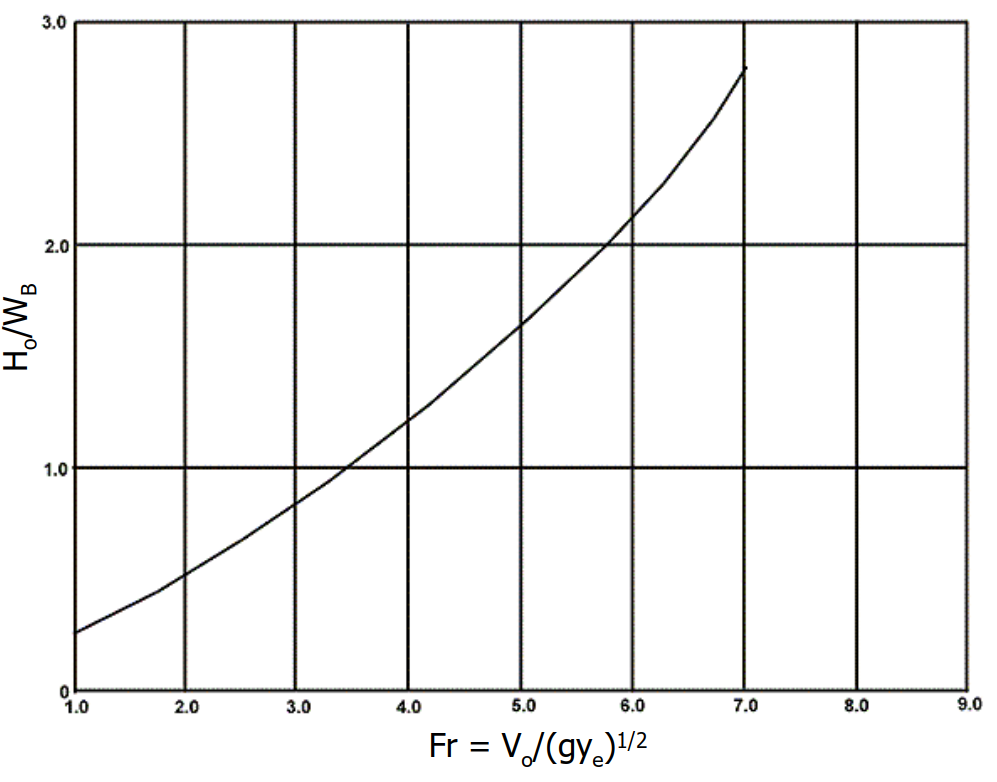
Thông tin thiết kế được trình bày dưới dạng đường cong không thứ nguyên trong Hình 9.14. Đường cong này tổng hợp dữ liệu từ ASCE (1957) và kết quả từ các thí nghiệm bổ sung do Sở Công chánh thành phố Los Angeles thực hiện.

Đường cong thể hiện mối quan hệ giữa số Froude và tỷ số giữa năng lượng đầu vào tại cấu trúc với chiều rộng cần thiết của cấu trúc. Các thử nghiệm tại Los Angeles cho thấy rằng việc nội suy giới hạn dựa trên đường cong này là chấp nhận được.

Khi chiều rộng bể, \(W_B\), đã được xác định, nhiều kích thước khác thể hiện trong Hình 9.13 sẽ được lấy theo Bảng 9.2. Để sử dụng Bảng 9.2, làm tròn giá trị \(W_B\) đến mục gần nhất trong bảng để xác định các kích thước còn lại. Không cần nội suy.

Khi tính toán năng lượng và số Froude, cần xác định độ sâu tương đương của dòng chảy \(y_e = \sqrt{A/2}\), tại vị trí dòng chảy đi vào cấu trúc từ một ống hoặc kênh có tiết diện không đều. Nói cách khác, diện tích tiết diện dòng chảy trong ống được quy đổi thành tiết diện chữ nhật tương đương có chiều rộng gấp đôi chiều sâu dòng chảy. Đoạn ống dẫn vào cấu trúc này có thể là kênh hở, kênh kín hoặc có bất kỳ hình dạng tiết diện nào.

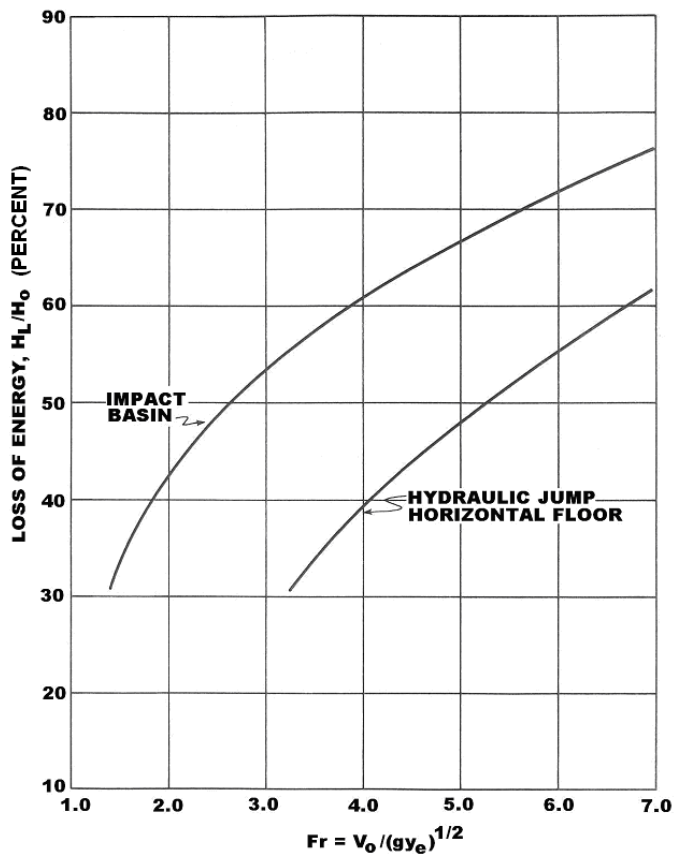
Hiệu quả của cấu trúc này được thể hiện rõ nhất khi so sánh tổn thất năng lượng trong cấu trúc với một cú nhảy thủy lực tự nhiên, như minh họa trong Hình 9.15. Tổn thất năng lượng được tính dựa trên đo đạc độ sâu và vận tốc tại ống vào và tại kênh hạ lưu không có mực nước hạ lưu (tailwater). So với cú nhảy thủy lực tự nhiên, bể tiêu năng kiểu VI của USBR thể hiện khả năng tiêu năng vượt trội hơn.

Mặc dù tailwater không bắt buộc để cấu trúc hoạt động hiệu quả, một mức tailwater vừa phải sẽ cải thiện hiệu suất. Để đạt hiệu quả tối ưu, nên thiết kế bể sao cho mực nước tailwater tối đa không vượt quá \(h_3 + \frac{h_2}{2}\), tức là bằng một nửa chiều cao tấm chắn đứng.

Đáy bể nên được xây dựng nằm ngang và có thể hoạt động hiệu quả với ống dẫn đầu vào có độ dốc đến 15° (27%). Với các ống dẫn vào có độ dốc lớn hơn 15°, nên bổ sung một đoạn ống nằm ngang dài tối thiểu bằng bốn lần chiều rộng ống, đặt ngay trước cấu trúc tiêu năng. Thực tế cho thấy rằng, ngay cả với các ống có độ dốc nhỏ hơn 15°, hiệu suất vẫn được cải thiện khi sử dụng đoạn ống nằm ngang như khuyến nghị cho trường hợp dốc hơn. Trong mọi trường hợp, cần duy trì đúng vị trí đáy vào (entrance invert) như thể hiện trong Hình 9.13.

Nếu đoạn ống nằm ngang được bố trí trước thiết bị tiêu năng, cần phân tích để xác định xem có hình thành cú nhảy thủy lực bên trong ống hay không. Khi dự đoán sẽ có bước nhảy thủy lực và dòng chảy tại cửa ra ống là đầy, thì nên lắp đặt một lỗ thông hơi (vent) có đường kính bằng khoảng một phần sáu đường kính ống tại vị trí thích hợp phía thượng lưu của điểm nhảy.

Để gia cố kết cấu cho tấm chắn treo, nên bố trí một gối đỡ ngắn bên dưới trung tâm của vách chắn. Gối đỡ này cũng đóng vai trò như một phần tử bổ sung tiêu năng cho dòng chảy.

Bảng 9.2 (SI). Kích thước USBR Type VI Impact Basin (m) (AASHTO, 1999)

Kích thước hình học chính

\(W_B\)	\(h_1\)	\(h_2\)	\(h_3\)	\(H_4\)	L	\(L_1\)	\(L_2\)
1.0	0.79	0.38	0.17	0.43	1.40	0.59	0.79
1.5	1.16	0.57	0.25	0.62	2.00	0.88	1.16
2.0	1.54	0.75	0.33	0.83	2.68	1.14	1.54
2.5	1.93	0.94	0.42	1.04	3.33	1.43	1.93
3.0	2.30	1.12	0.50	1.25	4.02	1.72	2.30
3.5	2.68	1.32	0.58	1.46	4.65	2.00	2.68
4.0	3.12	1.51	0.67	1.67	5.33	2.28	3.08
4.5	3.46	1.68	0.75	1.88	6.00	2.56	3.46
5.0	3.82	1.87	0.83	2.08	6.52	2.84	3.82
5.5	4.19	2.03	0.91	2.29	7.29	3.12	4.19
6.0	4.60	2.25	1.00	2.50	7.98	3.42	4.60

Chi tiết cấu tạo tường, rãnh, lớp đệm (tính theo mét)

\(W_B\)	\(W_1\)	\(W_2\)	\(t_1\)	\(t_2\)	\(t_3\)	\(t_4\)	\(t_5\)
1.0	0.08	0.26	0.15	0.15	0.15	0.15	0.08
1.5	0.13	0.42	0.15	0.15	0.15	0.15	0.08
2.0	0.15	0.55	0.15	0.15	0.15	0.15	0.08
2.5	0.18	0.68	0.16	0.18	0.18	0.16	0.08
3.0	0.22	0.83	0.20	0.20	0.20	0.20	0.08
3.5	0.26	0.91	0.20	0.23	0.23	0.21	0.10
4.0	0.30	0.91	0.20	0.28	0.25	0.25	0.10
4.5	0.36	0.91	0.20	0.30	0.30	0.30	0.13
5.0	0.39	0.91	0.22	0.31	0.30	0.30	0.15
5.5	0.41	0.91	0.22	0.33	0.33	0.33	0.18
6.0	0.45	0.91	0.25	0.36	0.35	0.35	0.19

Để giảm xói mòn và giúp bể hoạt động hiệu quả hơn, nên sử dụng phương án end sill thay thế và tường cánh (wingwall) nghiêng 45° như thể hiện trong Hình 9.13. End sill nên được đặt càng thấp càng tốt để tránh sự suy thoái phía hạ lưu. Để đạt hiệu quả tối ưu, đáy kênh hạ lưu nên có cao độ bằng với đỉnh của sill. Một rãnh (slot) nên được tạo tại end sill để thoát nước trong điều kiện dòng chảy thấp. Mặc dù bể được đặt thấp, rãnh này cho phép nước thấm ra đất xung quanh.

Để bảo vệ chống xói ngầm, cần xây một tường cutoff ở cuối bể. Chiều sâu của tường này phụ thuộc vào loại đất tại hiện trường. Riprap nên được bố trí phía hạ lưu bể với chiều dài ít nhất bằng bốn lần chiều rộng ống dẫn. Để biết khuyến nghị về kích thước riprap, tham khảo Chương 10.

Các thí nghiệm tại Los Angeles mô phỏng lưu lượng đến 11.3 m³/s và vận tốc dòng vào đến 15.2 m/s. Do đó, việc sử dụng bể này được giới hạn trong phạm vi các thông số đó. Vận tốc đến 15.2 m/s có thể sử dụng mà không gây tổn hại cấu trúc do xâm thực. Một số công trình hiện hữu vượt quá các giới hạn này, cho thấy có thể có sự linh hoạt trong thiết kế. Với những công trình lớn mà lưu lượng có thể phân chia, có thể sử dụng hai hay nhiều bể song song. Tuy nhiên, USBR Type VI không được khuyến nghị tại những nơi có mảnh vỡ hoặc đóng băng vì dễ gây nghẽn tắc nghiêm trọng.

Quy trình thiết kế được khuyến nghị cho USBR Type VI Impact Basin như sau:

Bước 1. Xác định lưu lượng thiết kế lớn nhất Q, vận tốc \(V_0\) và kiểm tra giới hạn thiết kế.
Tính diện tích dòng chảy tại cuối ống dẫn đầu vào A.
Tính độ sâu tương đương: \(y_e = \sqrt{A/2}\)

Bước 2. Tính số Froude và năng lượng tại cuối ống \(H_0\).

Bước 3. Xác định tỉ số \(H_0 / W_B\) từ Hình 9.14.

Tính chiều rộng bể yêu cầu \(W_B = \frac{H_0}{H_0/W_B}\)

Bước 4. Tra các kích thước còn lại từ Bảng 9.2 tương ứng với giá trị \(W_B\) đã tính được ở bước 3.

Bước 5. Xác định vận tốc tại cửa ra bể \(V_B = V_2\) bằng phương pháp thử – sai, sử dụng cân bằng năng lượng giữa cửa ra ống và cửa ra bể.

Xem xét xem vận tốc này có chấp nhận được hay không và có cần riprap hạ lưu hay không (xem Chương 10).

Áp dụng phương trình năng lượng:

$$H_B = \frac{Q}{W_B V_B} + \frac{V_B^2}{2g} = H_0 \left(1 – \frac{H_L}{H_0} \right)$$

Đây là một phương trình bậc ba có ba nghiệm: hai dương, một âm.

• Nghiệm âm bị loại bỏ.
• Hai nghiệm dương: một tương ứng với dòng chảy dưới tới hạn, một trên tới hạn.
• Nếu không có hoặc rất ít tailwater, chọn nghiệm trên tới hạn.
• Nếu tailwater đủ lớn, chọn nghiệm dưới tới hạn.

Ví dụ thiết kế: USBR Type VI Impact Basin (SI)

Xác định kích thước bể tiêu năng Type VI của USBR để sử dụng tại cửa ra của ống bê tông.
So sánh thiết kế với một cấu trúc tiêu năng tại cuối kênh chữ nhật bê tông.

Cho:

• D=1.219 m (đường kính ống và chiều rộng kênh)
• \(S_o = 0.15 \, \text{m/m}\)
• \(Q = 8.5 \, \text{m}^3/\text{s}\) (ống)
• \(Q = 10.6 \, \text{m}^3/\text{s}\) (kênh)
• n = 0.015
• \(V_0 = 12.192 \, \text{m/s}\)
• \(y_0 = 0.701 \, \text{m}\) (cho cả ống và kênh)

Giải:
Thiết kế bể tiêu năng đầu tiên cho ống tròn.

Bước 1.

Xác định lưu lượng cực đại Q, vận tốc \(V_0\).

Tính diện tích dòng chảy tại cuối ống dẫn đầu vào A.

Tính độ sâu tương đương \(y_e = \sqrt{A/2}\)

• Vì \(Q < 11.3 \, \text{m}^3/s \) và \(V_0 < 15.2 \, \text{m/s}\), có thể sử dụng bể tiêu năng tại vị trí này.
• \(A = Q / V_0 = 8.5 / 12.192 = 0.697 \, \text{m}^2\)
• \(y_e = \sqrt{A / 2} = \sqrt{0.697 / 2} = 0.590 \, \text{m}\)

Bước 2.

Tính số Froude và năng lượng tại cuối ống \(H_0\)

$$Fr = \frac{V_0}{\sqrt{g y_e}} = \frac{12.192}{\sqrt{9.81 \times 0.590}} = 5.07$$

$$H_0 = y_e + \frac{V_0^2}{2g} = 0.590 + \frac{(12.192)^2}{19.62} = 8.166 \, \text{m}$$

Bước 3.

Xác định \(H_0 / W_B\) từ Hình 9.14.

Tính chiều rộng bể yêu cầu \(W_B\):

$$W_B = \frac{H_0}{H_0 / W_B} = \frac{8.166}{1.68} = 4.86 \, \text{m}$$

Bước 4.
Tra các kích thước còn lại của bể USBR Type VI từ Bảng 9.2 với \(W_B = 5.0 \, \text{m}\) (làm tròn đến 0.5 m gần nhất)

Bước 5.
Xác định vận tốc ra bể \(V_B = V_2\) bằng phương pháp thử và sai, dùng cân bằng năng lượng:

$$H_B = \frac{Q}{W_B V_B} + \frac{V_B^2}{2g} = H_0 \left(1 – \frac{H_L}{H_0} \right)$$

Thay số:

$$H_B = \frac{8.5}{5.0 V_B} + \frac{V_B^2}{19.62} = 8.166(1 – 0.67) = 2.695$$

=> Dùng thử – sai, ta được \(V_B = 6.9 \, \text{m/s}\)

Vì không có tailwater, chọn nghiệm trên tới hạn. Vận tốc đã được giảm từ 12.2 m/s xuống còn 6.9 m/s.

So sánh thiết kế bể tiêu năng USBR Type VI giữa ống tròn và kênh chữ nhật

Một bể USBR Type VI thứ hai được thiết kế tại cuối kênh bê tông hình chữ nhật dài để so sánh với thiết kế dành cho ống tròn. Các kết quả tính toán và so sánh được trình bày trong bảng dưới đây với chiều rộng bể \(W_B = 5.5 \, \text{m}\):

Thông số	Ống tròn (Circular Pipe)	Kênh chữ nhật (Rectangular Channel)
Độ sâu dòng \(y_0 (m)\)	0.701	0.701
Diện tích dòng A (m²)	0.697	0.855
Vận tốc \(V_0\) (m/s)	12.192	12.419
Độ sâu tương đương \(y_e\) (m)	0.590	0.701
Cột vận tốc \(V_0^2 / 2g\) (m)	7.576	7.861
Tổng năng lượng \(H_0\) (m)	8.166	8.562
Số Froude	5.07	4.74
\(H_0 / W_B\) từ Hình 9.14	1.68	1.55
Chiều rộng bể \(W_B\) (m)	5.0	5.5
\(H_L / H_0\) từ Hình 9.15	67%	65%

Nhận xét:

• Vận tốc và tổng năng lượng đầu vào của kênh chữ nhật cao hơn một chút.
• Kênh chữ nhật yêu cầu chiều rộng bể lớn hơn để đạt hiệu quả tương đương.
• Hiệu suất tiêu tán năng lượng (thể hiện qua tỉ số \(H_L / H_0)\) của hai cấu hình là tương đương (65–67%).