- 4.1 Giới thiệu
- 4.2 Dòng chảy trong kênh phù sa
- 4.3 Dòng chảy ổn định đều
- 4.4 Dòng chảy không ổn định
- 4.5 Dòng chảy ổn định không đều
- 4.6 Dòng chảy Ổn Định Thay Đổi Nhanh (Steady Rapidly Varied Flow)
- 4.7 Dòng chảy Thay Đổi Chậm (Garadually varied flow)
4.1 Giới thiệu
Dòng chảy hở phức tạp hơn so với dòng chảy trong ống kín đầy nước, vì mực nước được xác định bởi các yếu tố chuyển động của dòng chảy. Ngoài ra, nếu đáy kênh có thể biến đổi (như sông tự nhiên), thì yếu tố biến đổi địa hình đáy kênh làm tăng thêm độ phức tạp. Trong trường hợp kênh có thể di chuyển, lực cản của dòng chảy cũng phụ thuộc vào chính dòng chảy đó.
Trong chương này, chúng ta sẽ trình bày các khái niệm và phương trình áp dụng cho điều kiện dòng chảy đơn giản nhất (dòng chảy ổn định, đồng nhất), cũng như các dạng địa hình đáy kênh thường gặp trong tự nhiên như sông.
Ngoài ra, các điều kiện dòng chảy và phương trình giải quyết các bài toán có mức độ phức tạp tăng dần cũng sẽ được đề cập. Phương pháp một chiều sẽ được sử dụng để mô tả các phương trình.
(nd: một số định nghĩa)
Dòng chảy hở: Dòng chảy xảy ra trong các kênh, sông, suối, nơi mặt trên của chất lỏng tiếp xúc với không khí.
Kênh phù sa: Kênh có đáy và bờ được cấu tạo bởi vật liệu dễ bị xói mòn như cát, bùn.
Dòng chảy ổn định: Dòng chảy mà các thông số như vận tốc, lưu lượng không thay đổi theo thời gian tại một điểm bất kỳ trong dòng chảy.
Dòng chảy đều: Dòng chảy mà các thông số thủy lực không thay đổi theo chiều dài của dòng chảy.
Phương pháp một chiều: Phương pháp giải toán trong đó chỉ xét sự thay đổi của các đại lượng theo một hướng duy nhất (thường là theo chiều dài của kênh).
4.2 Dòng chảy trong kênh phù sa
4.2.1 Kênh phù sa
Kênh phù sa là các kênh được hình thành từ vật liệu có thể bị vận chuyển bởi dòng chảy. Chúng thường bao gồm vật liệu đáy là cát, sỏi, hoặc đá cuội.
Những vật liệu này đóng vai trò quan trọng trong thiết kế thoát nước, vì chúng ảnh hưởng đến sức cản dòng chảy và xói mòn. Ngay cả các kênh bê tông và cống cũng có thể có biên dòng chảy phù sa do sự lắng đọng của vật liệu trong đáy cống.
4.2.2 Hình thái đáy kênh cát
Trong các dòng sông có đáy cát, vật liệu chính của đáy sông dao động từ bùn thô đến cát. Mặc dù có thể có các hạt mịn hoặc thô hơn, nhưng kích thước hạt chủ yếu vẫn là cát (chiếm ít nhất 50%).
Trong các dòng sông có đáy cát, vật liệu đáy dễ bị xói mòn và liên tục bị dòng chảy di chuyển và tái định hình.
Sự tương tác giữa dòng nước mang trầm tích và đáy cát tạo ra các dạng địa hình đáy khác nhau, làm thay đổi:
- Sức cản dòng chảy,
- Vận tốc nước,
- Độ cao mặt nước,
- Vận chuyển bùn cát.
Do đó, cần hiểu rõ các hình thái đáy sẽ xuất hiện để có thể ước tính sức cản dòng chảy, từ đó tính toán mực nước lũ, độ sâu dòng chảy và biên dạng mặt nước nhằm thiết kế các kênh thoát nước hiệu quả.
4.2.3 Chế độ dòng chảy
Dòng chảy trong các kênh phù sa được chia thành hai chế độ, ngăn cách bởi một vùng chuyển tiếp. Các hinh thái đáy kênh cát được thể hiện trong Hình 4.1. Các chế độ dòng chảy gồm:
- Chế độ dòng chảy thấp, trong đó lực cản dòng chảy lớn và vận chuyển bùn cát nhỏ. Dạng đáy kênh có thể là gợn (ripple) hoặc cồn (dune), hoặc sự kết hợp của cả hai (dunes with ripples superposed). Mặt nước không đồng pha với bề mặt đáy, và có vùng tách dòng tương đối lớn phía sau đỉnh của mỗi ripple hoặc dune (hình 4.1-2). Vận tốc chuyển động xuôi dòng của các ripple hoặc dune phụ thuộc vào chiều cao của chúng và vận tốc của các hạt di chuyển lên phía sau.
- Vùng chuyển tiếp, trong đó hình thái đáy có thể thay đổi từ dạng đặc trưng của chế độ dòng chảy thấp sang dạng đặc trưng của chế độ dòng chảy cao, chủ yếu phụ thuộc vào điều kiện ban đầu. Nếu hình thái đáy ban đầu là dune, độ sâu hoặc độ dốc có thể được tăng lên tới các giá trị phù hợp với chế độ dòng chảy cao mà không cần thay đổi hình thái đáy; ngược lại, nếu hình thái đáy ban đầu là phẳng, độ sâu và độ dốc có thể được giảm xuống tới các giá trị phù hợp với chế độ dòng chảy thấp mà không cần thay đổi hình thái đáy.
Lực cản dòng chảy và vận chuyển bùn cát cũng biến đổi tương ứng với sự thay đổi hình thái đáy trong vùng chuyển tiếp. Hiện tượng này có thể được giải thích bằng sự thay đổi lực cản dòng chảy, từ đó dẫn đến sự thay đổi độ sâu và độ dốc khi hình thái đáy thay đổi. - Chế độ dòng chảy cao (hình 4.1-6 & 7), trong đó lực cản dòng chảy nhỏ và vận chuyển bùn cát lớn. Hình thái đáy thường là phẳng hoặc antidune (cồn ngược). Mặt nước thường đồng pha với bề mặt đáy, trừ khi antidune bị phá vỡ, và thông thường dòng chảy không tách rời khỏi đáy.
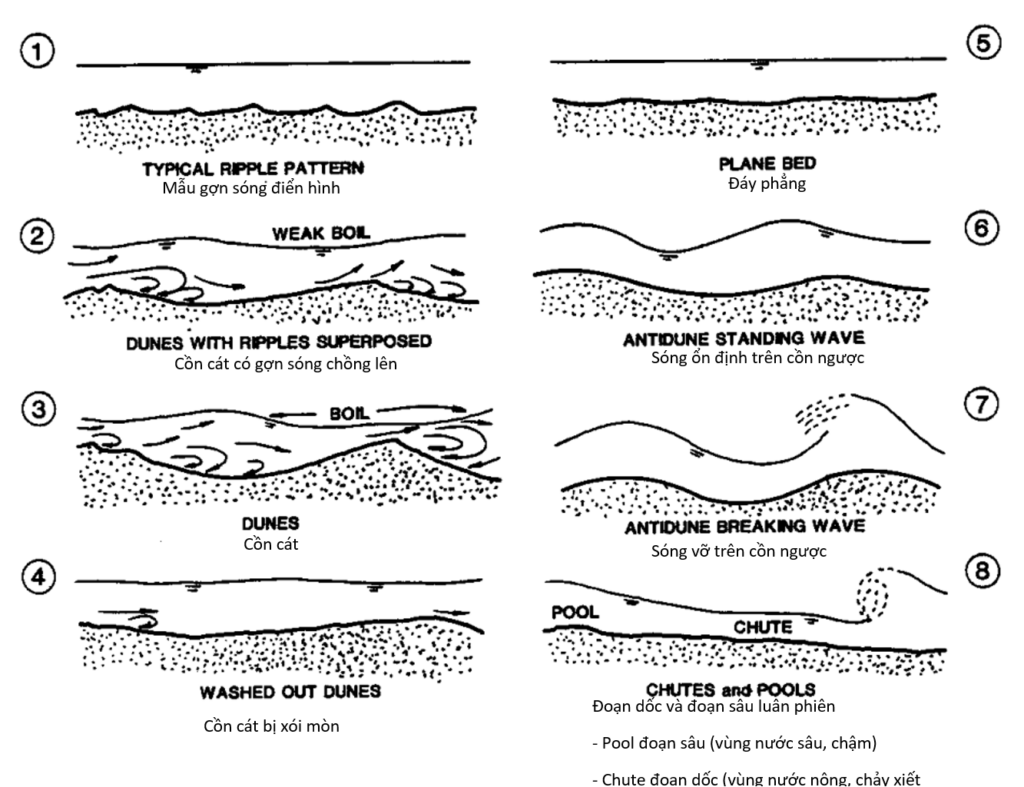
Sức cản dòng chảy đối với các hình thái đáy khác nhau và vật liệu đáy thô hơn sẽ được trình bày ở phần sau của mục này. Để biết thêm thông tin về vận chuyển bùn cát và các thông tin bổ sung về hình thái đáy, người đọc được giới thiệu đến HDS 6 (Richardson et al. 2001).
Khi lưu lượng lớn, hầu hết các kênh dòng có đáy cát chuyển từ dạng đáy dune sang vùng chuyển tiếp hoặc đáy phẳng. Nếu độ dốc lớn, antidune có thể xảy ra. Khi đó, sức cản dòng chảy sẽ giảm xuống còn một nửa đến một phần ba so với trước khi thay đổi dạng đáy. Việc tăng vận tốc và giảm độ sâu tương ứng có thể làm tăng xói mòn và khoét lở xung quanh các trụ cầu và mố cầu, đồng thời làm tăng kích thước cần thiết của lớp đá bảo vệ (riprap). Nếu dòng chảy chuyển sang dạng dòng antidune, có thể xuất hiện các tác động sóng đáng kể.
(nd: giải thích thêm về hình thái đáy)
Không nhất thiết một con sông luôn “một nửa chế độ thấp – vùng chuyển tiếp – một nửa chế độ cao”. “Hai chế độ và vùng chuyển tiếp” là cách mô tả trạng thái đáy theo điều kiện thủy lực (lực kéo đáy, độ sâu, dốc, hạt…); chúng có thể biểu hiện theo không gian hoặc theo thời gian – tùy tình huống.
Bạn có thể gặp ba kiểu điển hình:
- Đồng nhất theo không gian (một chế độ trên cả đoạn)
Nếu bề rộng, độ sâu, dốc và vật liệu khá đồng đều, cả đoạn có thể toàn chế độ thấp (ripples/dunes) hoặc toàn chế độ cao (plane bed/antidunes). Lúc này không nhìn thấy “vùng chuyển tiếp” trong không gian. - Khảm theo không gian (vá chắp nhiều mảng)
Ở nơi có thay đổi hình học/hydraulic (thu hẹp, mở rộng, dốc đổi, công trình…), một số đoạn có dune, đoạn khác plane bed/antidune. Giữa hai đoạn sẽ có một vùng ngắn nơi điều kiện đang “lửng lơ” → đó là vùng chuyển tiếp trong không gian. - Chuyển tiếp theo thời gian tại một mặt cắt
Khi lưu lượng tăng trong trận lũ, cùng một vị trí có thể đi qua chuỗi: ripples → dunes → washed-out dunes → plane bed → antidunes. Khi lưu lượng giảm, nó đi ngược lại, nhưng không trùng hệt mức ngưỡng do hysteresis (phụ thuộc tiền trạng/“antecedent bed”): đáy đang là dune có thể tồn tại thêm dù điều kiện đã tiệm cận chế độ cao, và ngược lại. Ở đây “vùng chuyển tiếp” là một khoảng thời gian chứ không phải một dải cố định theo chiều dài sông.
Vì vậy, trong không gian tham số (shear, độ sâu, dốc…) có hai miền ổn định của dạng đáy, và tồn tại một dải điều kiện chuyển tiếp nơi kết quả phụ thuộc vào tiền trạng đáy. Trên thực địa, bạn có thể thấy:
- Một chế độ chiếm ưu thế trên cả đoạn; hoặc
- Các mảng khác chế độ với đoạn ngắn chuyển tiếp giữa chúng; hoặc
- Một điểm duy nhất nhưng thay đổi theo thời gian khi thủy lực biến động.
Quy tắc nhớ nhanh
+ Vùng chuyển tiếp: dải điều kiện mà cùng một điều kiện có thể cho hai kết quả khác nhau tùy antecedent bed.
+ Chế độ thấp: sức cản lớn, vận chuyển nhỏ; bedform chính: ripples/dunes; mặt nước lệch pha với mặt đáy.
+ Chế độ cao: sức cản nhỏ, vận chuyển lớn; bedform chính: plane bed/antidunes; mặt nước đồng pha với mặt đáy (trừ khi antidune vỡ).
(nd: Dune, Atidune, Standing waver)
Dune: hình thành khi dòng chảy dưới tới hạn (subcritical), cát đẩy trôi về hạ lưu.
- Cấu tạo: Là các đụn cát lớn hình thành dưới đáy sông hoặc kênh do trầm tích bị vận chuyển và lắng đọng. Trên bề mặt các cồn này có thể xuất hiện các gợn nhỏ hơn (ripples).
- Hướng di chuyển: Di chuyển về phía hạ lưu (cùng chiều dòng chảy).
- Dòng chảy: Dòng chảy phía trên tạo xoáy cuộn nhẹ (weak boil), vận tốc không quá lớn.
- Điều kiện hình thành: Tốc độ dòng chảy vừa phải (dưới vận tốc tới hạn).
Antidune: hình thành khi dòng chảy siêu tới hạn (supercritical), và cát bị nâng lên ngược dòng hoặc dao động tại chỗ. Là dạng địa hình đáy hình thành dưới điều kiện dòng chảy siêu tới hạn (supercritical flow, Fr > 1)
- Cấu tạo: Là các dạng cồn ngược hướng với dòng chảy, thường có hình dạng đối xứng hơn và ít dốc.
- Hướng di chuyển: Khác với dune, antidune di chuyển ngược dòng hoặc có thể dao động tại chỗ (standing wave).
- Dòng chảy: Dòng chảy phía trên rất mạnh, có thể đạt hoặc vượt vận tốc tới hạn (supercritical flow).
- Hiện tượng sóng: Có thể xuất hiện các standing wave ở mặt nước trên các antidune này (như mô tả trong hình).
- Điều kiện hình thành: Vận tốc dòng chảy cao, điều kiện siêu tới hạn (Fr > 1).
Standing wave: Là dạng sóng không di chuyển, đỉnh và đáy sóng dao động tại chỗ như thể “đứng yên”; hình thành phía trên các antidune, thường ổn định tạm thời, rồi biến mất khi điều kiện dòng chảy thay đổi; xuất hiện ở mặt thoáng nước do tác động tương hỗ giữa dòng chảy mạnh và hình dạng đáy sông (antidune)
| Đặc điểm | Dune | Antidune |
|---|---|---|
| Hướng di chuyển | Theo dòng chảy | Ngược dòng hoặc dao động tại chỗ |
| Dạng dòng chảy | Tới hạn hoặc dưới tới hạn | Siêu tới hạn (supercritical) |
| Hiện tượng mặt nước | Mặt nước phẳng hoặc có sóng nhỏ | Standing wave |
| Ổn định | Tương đối ổn định | Thường không ổn định |
4.2.4 Vật liệu đáy thô
Ở lưu lượng thấp, vật liệu thô ở đáy sông phù sa có thể không di chuyển, nhưng ở lưu lượng trung bình hoặc lớn, vật liệu có thể bắt đầu di chuyển. Khi vật liệu thô ở đáy di chuyển, các dải cát hoặc sỏi có thể hình thành và tồn tại ở lưu lượng thấp. Những dải này có thể làm đổi hướng dòng chảy và gây ra xói bờ, hố xói và làm tắc nghẽn các kênh thoát nước.
Sức cản đối với dòng chảy do vật liệu thô ở đáy gây ra là do độ nhám hạt của vật liệu và tổn thất hình dạng do các dải gây ra. Tuy nhiên, vật liệu thô ở đáy trong các kênh thoát nước có thể mang lại hiệu quả tích cực bằng cách giảm xói mòn nhờ vào quá trình bảo vệ bề mặt đáy. Thông tin về quá trình bảo vệ này được trình bày trong HEC-20 (Lagasse et al. 2001) và HDS 6 (Richardson et al. 2001). Việc xác định hệ số Manning’s n cho vật liệu ở đáy sẽ được trình bày sau.
4.3 Dòng chảy ổn định đều
Trong dòng chảy ổn định, đều trong kênh hở, không có gia tốc, các đường dòng chảy là thẳng và song song, và phân bố áp suất là thủy tĩnh. Độ dốc của mặt nước Sw, mặt đáy So, và năng lượng Sf là bằng nhau (Hình 3.2). Đây là điều kiện dòng chảy đơn giản nhất để phân tích. Dòng chảy đều ổn định là một khái niệm lý tưởng trong dòng chảy kênh hở và khó đạt được ngay cả trong các máng thử nghiệm.
Trong nhiều ứng dụng, dòng chảy về cơ bản là ổn định và các thay đổi về chiều rộng, chiều sâu hoặc hướng chảy (dẫn đến dòng chảy không đều) là rất nhỏ nên dòng chảy có thể được coi là đều. Trong các trường hợp khác, các thay đổi diễn ra trên một khoảng cách rất dài khiến dòng chảy trở thành dòng chảy biến đổi dần.
Chiều sâu trong dòng chảy ổn định đều được gọi là normal depth và ký hiệu là yo. Vận tốc (V) thường được ký hiệu với cùng chỉ số dưới, tức là Vo. Các biến khác quan trọng trong dòng chảy đều ổn định là (1) lưu lượng (Q), (2) phân bố vận tốc theo phương thẳng đứng vy, (3) tổn thất năng lượng hL theo chiều dài đoạn chảy, và (4) ứng suất cắt, cả tại đáy và trên mặt, τo. Tất cả các biến này có mối liên hệ lẫn nhau.
Trong phần lựa chọn thiết kế, các phương trình kỹ thuật sẽ được đưa ra cùng với các ví dụ áp dụng để xác định giá trị các biến này.
(nd: ý nghĩa của normal depth)
Normal Depth là một khái niệm quan trọng trong các tính toán thủy lực sau này! Giá trị Normal Depth chỉ có khi “dòng chảy đều ổn định” như đã nêu ở trên, do đó giá trị này trong thực tế rất khó xẩy ra! Tuy nhiên, ý nghĩa lý thuyết của nó rất quan trọng vì từ đó các tính toán thủy lực trở nên đơn giản hơn nhiều! Các thử nghiệm đã cho thấy sai số từ cách đơn giản hóa như vậy là có thể chấp nhận được trong thực tế.
4.3.1 Phương trình Manning cho Vận tốc Trung bình và Lưu lượng
Nước chảy trong kênh thoát nước có độ dốc là do tác động của trọng lực. Dòng chảy bị cản trở bởi ma sát giữa nước và bề mặt ướt của kênh. Lưu lượng dòng chảy (Q), độ sâu dòng chảy (y), và vận tốc dòng chảy (V) phụ thuộc vào hình dạng kênh, độ nhám (n), và độ dốc đáy kênh (S₀).
Nhiều phương trình đã được thiết lập để xác định vận tốc và lưu lượng trong kênh hở. Một phương trình quan trọng và được sử dụng rộng rãi là phương trình Manning, đặt theo tên Robert Manning, một kỹ sư người Ireland. Phương trình Manning để tính vận tốc dòng chảy trong kênh hở được viết như sau:
$$V = \frac{K_u}{n} \, R^{2/3} \, S^{1/2} \tag{4.1}$$
trong đó:
- V = Vận tốc trung bình, m/s (ft/s)
- n = Hệ số nhám Manning của kênh
- R = Bán kính thủy lực, m (ft)
- S = Độ dốc năng lượng, m/m (ft/ft), đối với dòng chảy ổn định đồng nhất, S = S₀ (độ dốc đáy kênh)
- Kₙ = Hệ số chuyển đổi đơn vị, bằng 1 trong hệ SI (1.49 trong hệ Anh)
Trong nhiều thập kỷ qua, các giá trị Manning’s n tiêu biểu đã được tổng hợp, giúp kỹ sư ước tính giá trị phù hợp dựa trên đặc điểm chung của bề mặt kênh. Hầu hết các sách giáo khoa thủy lực và hướng dẫn thiết kế thoát nước đều cung cấp bảng tra giá trị Manning’s n tiêu biểu.
Danh sách rút gọn của các hệ số nhám Manning có thể được tìm thấy trong Phụ lục B, Bảng B.2. Ngoài ra, cũng có nhiều tài liệu minh họa bằng hình ảnh về các giá trị Manning’s n cho các loại kênh và vùng ngập lũ khác nhau (Barnes, 1967; Acrement & Schneider, 1984). Đối với kênh có độ dốc rất lớn, cần có các điều chỉnh đặc biệt (Jarrett, 1985). Một phương pháp xác định n theo hướng số học là:
- Chọn giá trị nhám cơ bản cho một kênh thẳng, đồng nhất và trơn nhẵn với vật liệu tương ứng.
- Bổ sung các yếu tố nhám bổ sung để phù hợp với đặc điểm thực tế của kênh.
$$n = (n_0 + n_1 + n_2 + n_3 + n_4) \, m_5 \tag{4.2}$$
trong đó:
- n₀ = Giá trị nhám cơ bản cho kênh thẳng và đồng nhất
- n₁ = Giá trị cộng thêm do sự không đều của mặt cắt ngang
- n₂ = Giá trị cộng thêm do biến đổi trong hình dạng kênh
- n₃ = Giá trị cộng thêm do vật cản trong kênh
- n₄ = Giá trị cộng thêm do thảm thực vật trong kênh
- m₅ = Hệ số nhân do độ uốn khúc của kênh
Phương pháp này và các hệ số liên quan được thảo luận trong Cowan (1956) và Chow (1959). Phương pháp này có thể hữu ích đối với kênh tự nhiên, nhưng ít được áp dụng trong thiết kế thoát nước đường giao thông.
Đối với kênh có lớp đá bảo vệ (rock riprap channels), hệ số Manning’s n thường được biểu diễn như một hàm của kích thước đá. Một số phương trình xác định Manning’s n cho kênh đá bảo vệ được trình bày trong HEC-15, bao gồm:
$$n = \frac{K_u \, y^{1/6}}{2.25 + 5.23 \log \left( \frac{y}{D_{50}} \right)} \tag{4.3}$$
trong đó:
- y = Độ sâu trung bình của dòng chảy trong kênh, m (ft)
- D₅₀ = Kích thước trung bình của đá bảo vệ/sỏi, m (ft)
- Kᵤ = Hằng số chuyển đổi đơn vị, 0.319 (hệ SI) và 2.262 (hệ Anh)
Phương trình này có hiệu lực khi tỷ số \(\frac{y}{D_{50}}\) nằm trong khoảng từ 1.5 đến 185, đây là phạm vi điển hình cho hầu hết các kênh thoát nước ven đường và kênh nhỏ khác. Đối với các điều kiện nằm ngoài phạm vi này, tham khảo HEC-15 để có phương pháp phù hợp hơn.
(nd: \(D_{50}\))
D50 là kích thước trung vị của đá hộc hoặc sỏi trong lòng kênh hoặc lớp bảo vệ bờ, nghĩa là:
- 50% khối lượng (hoặc thể tích) vật liệu có kích thước nhỏ hơn hoặc bằng giá trị D50.
- Đây là đại lượng phổ biến để đặc trưng kích thước trung bình của vật liệu đá trong các thiết kế công trình thủy như kênh, mái dốc, đê bảo vệ, hoặc lớp riprap chống xói.
Trong thực tế
- Nếu bạn lấy một mẫu riprap và sàng qua một loạt rây, kích thước D50 là kích thước lỗ rây mà tại đó 50% trọng lượng vật liệu đã lọt qua.
- Giá trị này dùng để ước tính độ nhám (Manning’s n), khả năng chống xói của lớp đá, hoặc để tính toán thủy lực như trong công thức
Độ nhám trên vùng ngập lũ phức tạp do sự xuất hiện của:
- Thảm thực vật,
- Địa hình tự nhiên và nhân tạo không đều,
- Công trình xây dựng,
- Hướng dòng chảy không xác định,
- Độ dốc thay đổi,
- Và nhiều yếu tố khác.
Các hệ số cản trở dòng chảy phản ánh những yếu tố này thường được xác định dựa trên kinh nghiệm thực tế với các điều kiện tương tự. Nhìn chung, sức cản dòng chảy trên vùng ngập lũ là rất lớn. Trong một số trường hợp, tình hình trở nên phức tạp hơn do:
- Sự lắng đọng trầm tích,
- Sự hình thành cồn cát và bãi bồi,
Những yếu tố này làm thay đổi sức cản dòng chảy và hướng dòng chảy.
Sự xuất hiện của băng làm thay đổi độ nhám kênh và sức cản dòng chảy theo nhiều cách khác nhau. Khi mặt nước bị đóng băng, dòng chảy hở sẽ gần giống như dòng chảy trong ống kín hơn. Lúc này, sẽ xuất hiện ứng suất cắt giữa nước chảy và mặt băng, làm thay đổi đặc tính thủy lực của kênh.
Lực cắt tại bề mặt băng lớn hơn nhiều so với ứng suất cắt thông thường phát sinh tại mặt phân cách không khí – nước. Mặt tiếp xúc băng – nước không phải lúc nào cũng nhẵn. Trong nhiều trường hợp, mặt dưới của lớp băng bị biến dạng, tạo thành các cấu trúc tương tự như gợn cát hoặc cồn cát quan sát thấy ở đáy kênh cát. Điều này có thể làm tăng thêm sức cản tổng thể của dòng chảy trong kênh. Khi có băng che phủ một phần hoặc toàn bộ, lực cản của băng làm chậm dòng chảy, giảm vận tốc trung bình và làm tăng độ sâu dòng chảy.
Bán kính thủy lực (R) là một hệ số hình dạng, chỉ phụ thuộc vào kích thước kênh và độ sâu dòng chảy. Giá trị này được tính theo phương trình:
$$R = \frac{A}{P} \tag{4.4}$$
trong đó:
- A = Diện tích mặt cắt dòng chảy, vuông góc với hướng dòng, m² (ft²)
- P = Chu vi ướt – chiều dài tiếp xúc ướt giữa dòng nước và lòng kênh, vuông góc với hướng dòng chảy
Lưu lượng xả (Q) được xác định theo phương trình liên tục (xem Chương 3):
$$Q = V A$$
trong đó:
- Q = Lưu lượng xả, m³/s (ft³/s)
- A = Diện tích mặt cắt dòng chảy, m² (ft²)
- V = Vận tốc trung bình, m/s (ft/s)
Kết hợp phương trình (4.1) và (4.4), ta có thể tính trực tiếp lưu lượng theo phương trình Manning:
$$Q = \frac{K_u}{n} A R^{2/3} S^{1/2} \tag{4.5}$$
Trong một số phép tính, các đặc tính mặt cắt được gom lại thành một đại lượng gọi là hệ số dẫn nước (conveyance), ký hiệu là K:
$$K = \frac{K_u}{n} A R^{2/3} \tag{4.6}$$
Khi đó:
$$Q = K S^{1/2} \tag{4.7}$$
Khi một mặt cắt ngang kênh có hình dạng không đều, chẳng hạn như một kênh chính hẹp và sâu cùng với vùng ngập tràn rộng và nông, thì mặt cắt phải được chia nhỏ và dòng chảy phải được tính riêng biệt cho kênh chính và vùng ngập tràn. Quy trình tương tự cũng được áp dụng khi các phần khác nhau của mặt cắt ngang có hệ số nhám khác nhau. Khi tính bán kính thủy lực của từng phần, độ sâu nước chung giữa hai phần liền kề sẽ không được tính là chu vi ướt (xem Ví dụ Bài toán 4.3).
Có thể tính toán năng suất truyền dẫn (conveyance) và vẽ đường cong cho bất kỳ mặt cắt kênh nào. Diện tích và bán kính thủy lực được tính toán cho các độ sâu giả định khác nhau, và giá trị tương ứng của K được tính từ phương trình. Các giá trị năng suất truyền dẫn được biểu diễn theo độ sâu dòng chảy và một đường cong mượt nối các điểm được vẽ chính là đường cong conveyance.
Nếu mặt cắt được chia nhỏ, thì năng suất truyền dẫn của từng phần (Ka, Kb,…Kn) sẽ được tính, và tổng conveyance của kênh là tổng conveyance của các phần. Lưu lượng sau đó có thể được tính bằng Phương trình 4.7. Ví dụ 4.3 minh họa đường cong conveyance cho một mặt cắt phức hợp.
Khái niệm conveyance của kênh rất hữu ích khi tính toán phân bố dòng chảy lũ tràn qua vùng ngập trong mặt cắt dòng và sự phân bố dòng chảy qua các lối mở trong một thiết kế vượt qua dòng nước. Dòng chảy qua mỗi lối có thể được giả định có tỷ lệ bằng với tỷ lệ lưu lượng tổng so với năng suất truyền dẫn của từng lối.
4.3.2 Hỗ trợ trong việc giải phương trình Manning
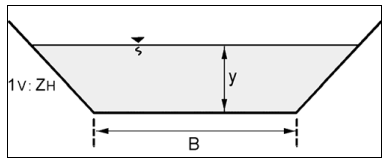
Các phương trình tính diện tích mặt cắt ngang (A), chu vi ướt (P), và bán kính thủy lực (R) cho kênh chữ nhật và kênh hình thang (Hình 4.2) được viết như sau:
$$A = By + Zy^2 \tag{4.8}$$
$$P = B + 2y \sqrt{1 + Z^2} \tag{4.9}$$
$$R = \frac{By + Zy^2}{B + 2y \sqrt{1 + Z^2}} \tag{4.10}$$
Trong đó:
- A = Diện tích mặt cắt dòng chảy, m²
- P = Chu vi ướt, m
- R = Bán kính thuỷ lực, m
- B = Đáy kênh ngang (chiều rộng đáy ngang), m
- y = Chiều sâu dòng chảy, m
- Z = Hệ số mái dốc hai bên (tức là mỗi bên nghiêng Z đơn vị ngang cho 1 đơn vị đứng)
(nd: thủy lực online)
WebSite hỗ trợ tính toán thủy lực cơ bản tại đây
Ví dụ 4.1 – Tính vận tốc và lưu lượng
Cho: Một kênh đất hình thang có các thông số sau:
- B = 2 m (chiều rộng đáy kênh)
- Độ dốc thành kênh = 1V:2H (tức là mỗi mét chiều cao tăng 2 mét chiều ngang)
- S = 0.003 m/m (độ dốc đáy kênh)
- Độ sâu dòng chảy đều ổn định (normal depth) y = 0.5 m
- n = 0.02 (hệ số nhám Manning)
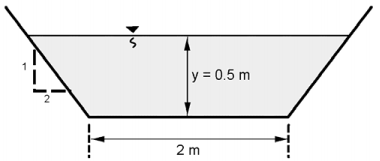
Hỏi: Vận tốc V và lưu lượng Q
Giải
$$V = \frac{K_u}{n} \, R^{2/3} \, S^{1/2}$$
Trong hệ SI: \(K_u = 1\)
$$R = \frac{By + Zy^2}{B + 2y\sqrt{1 + Z^2}} = \frac{2(0.5) + 2(0.5)^2}{2 + 2(0.5)\sqrt{1 + (2)^2}} = \frac{1.50}{4.24} = 0.35\, \text{m} $$
$$V = \left(\frac{1}{0.02}\right) \cdot (0.35^{2/3}) \cdot (0.003^{1/2}) = 1.36\, \text{m/s} $$
$$Q = V \cdot A = 1.36 \cdot \left[2(0.5) + 2(0.5)^2\right] = 2.0\, \text{m}^3/\text{s}$$
Ví dụ 4.2 – Tính độ sâu và vận tốc V
Cho: Một kênh bê tông hình thang có các thông số sau:
- B = 1.5 m (chiều rộng đáy kênh)
- Độ dốc thành kênh = 1V:2H (mỗi mét chiều cao tăng 2 mét chiều ngang)
- n = 0.013 (hệ số nhám Manning)
- Độ dốc đáy kênh = 0.002
- Lưu lượng dòng chảy = 3 m³/s
Hỏi: Độ sâu y và vận tốc V
Giải:
- Sử dụng phương trình Manning
$$Q = \frac{K_u}{n} A R^{2/3} S^{1/2}$$
với \(K_u = 1\) và các mối quan hệ cho A và R là:
$$A = By + Zy^2 = 1.5y + 2y^2$$
$$R = \frac{By + Zy^2}{B + 2y\sqrt{1 + Z^2}} = \frac{1.5y + 2y^2}{1.5 + 4.47y}$$
Thay A và R vào phương trình Manning:
$$Q = \left( \frac{1}{0.013} \right)(1.5y + 2y^2) \left( \frac{1.5y + 2y^2}{1.5 + 4.47y} \right)^{2/3} (0.002)^{1/2}$$
- Dùng phương pháp thử – sai để tìm giá trị y sao cho Q = 3 m³/s
Thử với y = 0.70:
$$Q = \left( \frac{1}{0.013} \right)(1.05 + 0.98) \left( \frac{1.05 + 0.98}{4.629} \right)^{2/3} (0.002)^{1/2} = 4.03 \, \text{m}^3/\text{s}$$
Vì 4.03 > 3.0, giá trị y giả định quá lớn. Hãy thử giá trị nhỏ hơn, ví dụ y = 0.60.
Thử với y = 0.60:
$$Q = \left( \frac{1}{0.013} \right)(0.9 + 0.72) \left( \frac{0.9 + 0.72}{4.18} \right)^{2/3} (0.002)^{1/2} = 2.96 \, \text{m}^3/\text{s}$$
Vì 2.96 ≈ 3.0, nên giá trị y giả định là hợp lý.
Vậy: sử dụng y=0.60 m, và dùng phương trình liên tục để tìm vận tốc
$$V = Q/A$$
$$V = \frac{3.0}{0.9 + 0.72} = 1.85 \, \text{m/s}$$
Ví dụ 4.3 – Tính lưu lượng kênh phức tạp
Cho: Một kênh phức hợp như hình minh họa, với các thông số sau:
- Hệ số nhám Manning (n) = 0.03
- Độ dốc dọc kênh = 0.002 m/m
- Độ dốc thành kênh = 1V:1H (mỗi mét chiều cao tăng 1 mét chiều ngang)
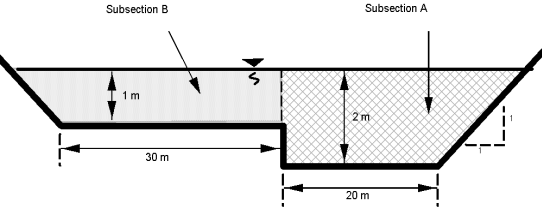
Hỏi: Lưu lượng Q
Giải:
1. Phần tiết diện A
A = (2)(20)+\(\frac{1}{2}\)(2)(2) = 42 m2
WP = 20 + 2(2)\(\frac{1}{2}\) +1 = 23.83 m
R = \(\frac{42}{23.83}\) = 1.76 m
V = \(\frac{1}{0.03}\)(1.76)2/3(0.002)1/2 = 2.17 m/s
Q = 42(2.17) = 91.17 m3/s
2. Phần tiết diện B
A = (30)(1)+\(\frac{1}{2}\)(1)(1) = 30.5 m2
WP = 30 + 1(2)\(\frac{1}{2}\) = 32.41 m
R = \(\frac{30.5}{31.41}\) = 0.97 m
V = \(\frac{1}{0.03}\)(0.97)2/3(0.002)1/2 = 1.46 m/s
Q = 30.5(1.46) = 44.53 m3/s
3. Đối với toàn bộ kênh
A = 42 + 30.5 = 72.5 m2
Q = 91.14 + 44.53 = 135.67 m3/s hay 136m3/s
4. Nếu kênh được xem xét như một tổng thể mà không chia nhỏ, kết quả thu được sẽ như sau.
A = 72.5m2
WP = 23.82+31.41=55.23m
R = 72.5/55.23 = 1.31m
V = (1/0.03)(1.31)2/3(0.002)1/2 = 1.78 m/s
Q = 72.5(1.78) = 129.05 m3/s
Lưu lượng tính toán khi sử dụng toàn bộ kênh nhỏ hơn đáng kể so với lưu lượng thu được khi chia nhỏ kênh để tính toán riêng từng phần.
5. Vẽ đường cong khả năng dẫn nước cho mặt cắt ngang này và tính tổng lưu lượng bằng Phương trình 4.7.
Với một mặt cắt được chia nhỏ, khả năng dẫn nước tại một độ sâu dòng chảy nhất định cần được tính riêng cho từng phần mặt cắt, sau đó cộng lại để thu được tổng khả năng dẫn nước tại độ sâu đó. Quá trình tính toán này và đồ thị khả năng dẫn nước được minh họa bên dưới:
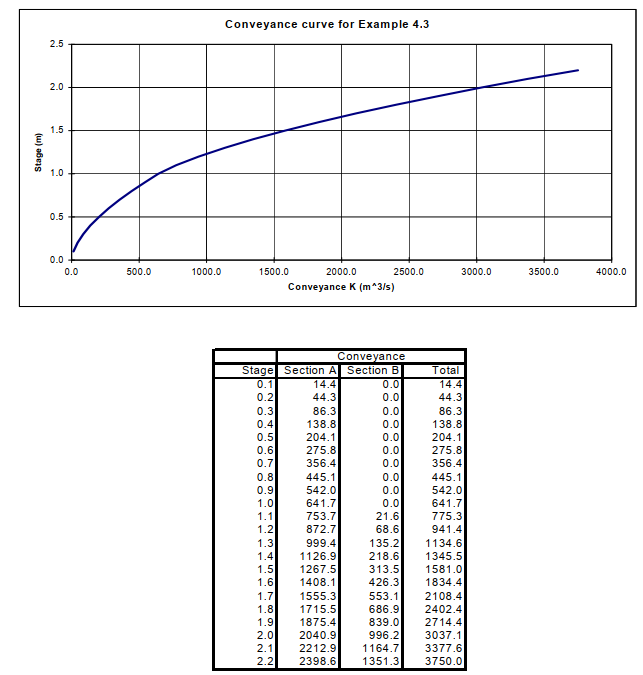
Ở độ sâu dòng chảy chính 2 m, tổng khả năng dẫn nước là 3037.1.
Tổng lưu lượng dòng chảy được tính theo Phương trình 4.7 như sau:
Q = K S1/2 = 3037.1(0.002)1/2 = 135.8 m3/s hay 136m3/s
Kết quả này khớp với giá trị lưu lượng đúng cho độ sâu dòng chảy 2 m, như đã tính toán ở mục 3 phía trên.
4.3.3 Phân bố vận tốc
Trong một số trường hợp, khi thiết kế công trình thoát nước đường giao thông, cần phải biết phân bố vận tốc theo phương thẳng đứng (ví dụ: khi thiết kế đá bảo vệ chống xói lở và kiểm soát xói mòn).
Do ảnh hưởng của độ nhám bề mặt đáy, vận tốc dòng chảy thay đổi theo phương thẳng đứng, từ giá trị nhỏ nhất gần đáy kênh đến giá trị lớn nhất gần mặt nước (Hình 4.3).
Trong phần này, sẽ trình bày dạng Einstein của phương trình phân bố vận tốc theo phương thẳng đứng dựa trên mô hình Karman-Prandtl, cũng như phương trình vận tốc trung bình trong dòng chảy ổn định đều (Einstein, 1950).
Để xem chi tiết quá trình suy diễn các phương trình này, người đọc có thể tham khảo các giáo trình cơ học chất lỏng tiêu chuẩn hoặc HDS 6 (Richardson et al., 2001).
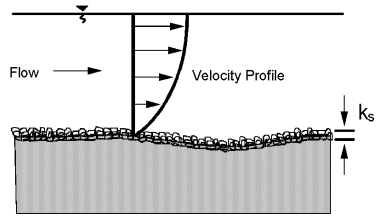
Các phương trình biểu diễn phân bố vận tốc (v) và vận tốc trung bình (V) có thể được viết dưới các dạng không thứ nguyên sau:
$$\frac{v}{V_*} = 5.75 \log \left(30.2 \, \frac{Xy}{k_s} \right) \tag{4.11}$$
và
$$\frac{V}{V_*} = 5.75 \log \left(12.27 \, \frac{Xy_0}{k_s} \right) \tag{4.12}$$
trong đó:
- X = Hệ số được cho trong Hình 4.4
- ks = Độ nhám đặc trưng, giá trị ks thay đổi từ D84 đối với kênh có đáy cát thuần, đến 3.5 lần D84 đối với dòng chảy có vật liệu đáy thô; trong ứng dụng thực tế, sử dụng 3.5 lần D84, đơn vị m (ft)
- y = Độ sâu đến vị trí cần xét, m (ft)
- v = Vận tốc trung bình tại độ sâu y, m/s (ft/s)
- yo = Độ sâu dòng chảy, m (ft)
- V = Vận tốc trung bình theo độ sâu, m/s (ft/s)
- V∗ = Vận tốc cắt, được tính theo (τo/ρ)1/2, m/s (ft/s)
- τo = Ứng suất cắt tại ranh giới, N/m² (lb/ft²)
- δ′ = Bề dày của lớp dưới nhớt, được tính theo 11.6μ/V∗, m (ft)
- μ = Độ nhớt động lực của nước, tham khảo Bảng A.6, đơn vị N·s/m² (lb·s/ft²)
- ρ = Mật độ của nước, đơn vị kg/m³ (lb·s²/ft⁴)
4.3.4 Ứng suất cắt
Ứng suất cắt (shear stress) là lực mà nước tác động lên đáy và bờ kênh khi nó chảy qua bề mặt này.
Các phương trình sau có thể được sử dụng để xác định ứng suất cắt tại ranh giới kênh, phát sinh do lực của dòng chảy. Để xem quá trình suy diễn các phương trình này, tham khảo các giáo trình cơ học chất lỏng hoặc HDS 6 (Richardson et al., 2001).
- Phương trình đầu tiên (Phương trình 4.13) là phương trình chính xác, cho ứng suất cắt trung bình trên chu vi ướt.
- Các phương trình tiếp theo là bán thực nghiệm, được suy ra từ việc giải phương trình vận tốc Karman-Prandtl.
$$\tau_o = \gamma \, R \, S_o \tag{4.13}$$
trong đó:
- τₒ = Ứng suất tiếp trung bình trên chu vi ướt, N/m² (lb/ft²)
- γ = Trọng lượng riêng của nước, N/m³ (lb/ft³)
- R = Bán kính thuỷ lực, m (ft)
- Sₒ = Độ dốc đáy kênh, m/m (ft/ft). Trong dòng chảy biến đổi dần, Sₒ là độ dốc của đường năng lượng, Sₒ = Sf
$$\tau_o = \frac{\rho (v_1 – v_2)^2}{\left[5.75 \log \left( \frac{y_1}{y_2} \right) \right]^2} \tag{4.14}$$
$$\tau_o = \frac{\rho V^2}{\left[5.75 \log \left(12.27 \, \frac{y_0}{k_s} \right) \right]^2} \tag{4.15}$$
trong đó:
- ρ = Khối lượng riêng của nước, kg/m³
- v₁, v₂ = Vận tốc tại hai điểm khác nhau trong dòng chảy
- V = Vận tốc trung bình của dòng chảy
- y₁, y₂, y₀ = Chiều sâu tại các vị trí tương ứng trong dòng chảy, m
- kₛ = Độ nhám tương đương, m
Ví dụ 4.4 – Tính ứng suất
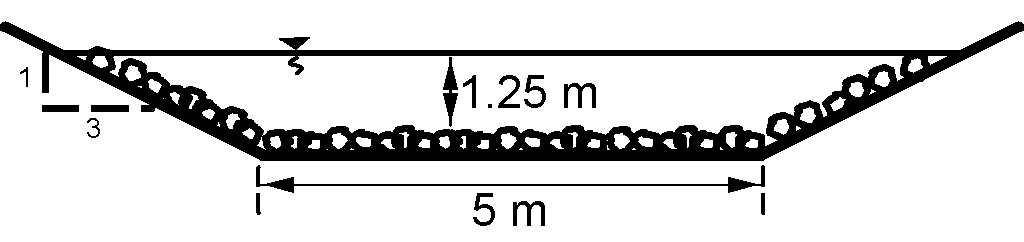
Ứng suất cắt dọc theo chu vi ướt của kênh hình thang; Ứng suất cắt tác động lên một hạt vật liệu nằm ở đáy kênh.
Cho:
- Kênh hình thang như minh họa
- Độ dốc đáy kênh (So) = 0.005
- Trọng lượng đơn vị của nước (γ) = 9800 N/m³
- Vận tốc trung bình (V) = 1.8 m/s
- Kích thước trung vị của hạt đáy (D84}) = 0.15 m
Hỏi:
- τo dọc theo chu vi ướt.
- τo dọc theo đáy kênh.
Giải:
(1) Ứng suất tiếp tuyến dọc theo chu vi ướt được xác định theo:
$$\tau_o = \gamma \, R \, S_0$$
trong đó:
$$R = \frac{A}{P}$$
$$A = 5 \cdot (1.25) + 3 \cdot (1.25)^2 = 10.94 \, \text{m}^2$$
$$P = 5 + 2(1.25)\sqrt{10} = 12.91 \, \text{m}$$
$$R = \frac{10.94}{12.91} = 0.85 \, \text{m}$$
$$\tau_o = 9800 \cdot 0.85 \cdot 0.005 = 41.7 \, \text{N/m}^2$$
(2) Ứng suất tiếp tuyến tại đáy tại một điểm được tính theo:
$$\tau_o = \frac{\rho V^2}{\left[5.75 \log \left(12.27 \frac{y_0}{k_s} \right)\right]^2} $$
$$\tau_o = \frac{1000 \cdot (1.8)^2}{\left[5.75 \log \left(12.27 \cdot \frac{1.25}{3.5 \cdot 0.15} \right)\right]^2} = 45.6 \, \text{N/m}^2$$
4.3.5 Số Froude và Mối Quan Hệ với Dòng Chảy Tới Hạn, Dưới Tới Hạn và Siêu Tới Hạn
Một tham số không thứ nguyên cực kỳ quan trọng trong dòng chảy hở là số Froude, được định nghĩa là tỷ số giữa lực quán tính và lực trọng trường.
Số Froude thường được biểu diễn dưới dạng:
$$Fr = \frac{V}{\sqrt{g y}} \tag{4.16}$$
Trong đó:
- Fr = Số Froude (Froude Number)
- V = Vận tốc dòng chảy, m/s (ft/s)
- g = Gia tốc trọng trường, m/s² (ft/s²)
- y = Chiều sâu dòng chảy, m (ft)
V và y có thể là vận tốc trung bình và độ sâu trong kênh hoặc là vận tốc và độ sâu theo phương thẳng đứng. Nếu dùng trung bình, thì Số Froude là cho điều kiện dòng chảy trung bình trong kênh. Nếu dùng tại một điểm cụ thể, thì đó là Số Froude tại một vị trí cụ thể trong mặt cắt ngang. Số Froude mô tả duy nhất kiểu dòng chảy trong dòng chảy kênh hở. Ví dụ, trong dòng chảy ở kênh phù sa với vật liệu đáy là cát, các gợn sóng và cồn chỉ hình thành khi Số Froude nhỏ hơn 1.0 (dòng chảy dưới tới hạn); trong khi đó, các sóng antidune chỉ hình thành khi Số Froude lớn hơn 1.0. Việc hình thành sóng dạng mặt phẳng là không phụ thuộc vào Số Froude. Số Froude là tham số tỷ lệ thường được sử dụng trong mô hình các dòng chảy kênh hở trong phòng thí nghiệm.
Khi Số Froude bằng 1.0, dòng chảy là tới hạn; giá trị của Số Froude lớn hơn 1.0 biểu thị dòng chảy siêu tới hạn hoặc dòng chảy nhanh, và nhỏ hơn 1.0 biểu thị dòng chảy dưới tới hạn hoặc dòng chảy yên tĩnh. Vận tốc và độ sâu tại dòng chảy tới hạn được gọi là vận tốc tới hạn và độ sâu tới hạn. Độ dốc kênh tạo ra độ sâu và vận tốc tới hạn được gọi là độ dốc tới hạn. Việc chuyển từ dòng chảy siêu tới hạn sang dòng chảy dưới tới hạn thường xảy ra đột ngột (đặc biệt khi Số Froude lớn hơn 2.0) và gây ra hiện tượng gọi là nhảy thủy lực (hydraulic jump).
Độ sâu và vận tốc tới hạn ứng với một lưu lượng cụ thể chỉ phụ thuộc vào kích thước và hình dạng của kênh, không phụ thuộc vào độ dốc kênh và độ nhám. Độ dốc tới hạn phụ thuộc vào độ nhám kênh, hình dạng kênh và lưu lượng dòng chảy. Với một độ sâu và vận tốc tới hạn cho trước, độ dốc tới hạn cho một độ nhám nhất định có thể được tính bằng phương trình Manning.
Dòng chảy siêu tới hạn khó kiểm soát vì sự thay đổi đột ngột về hướng hoặc hình dạng mặt cắt gây ra sóng di chuyển ngược dòng, luân phiên từ bên này sang bên kia, đôi khi khiến nước tràn qua các bờ kênh. Những thay đổi về hình dạng kênh, độ dốc, hướng chảy hoặc độ nhám không thể phản hồi ngược lên dòng chảy phía thượng lưu. Trong dòng chảy siêu tới hạn, việc kiểm soát dòng chảy là ở phía thượng lưu. Dòng chảy siêu tới hạn phổ biến ở các máng dốc, kênh và suối miền núi.
Dòng chảy dưới tới hạn tương đối dễ kiểm soát đối với các dòng chảy có Số Froude nhỏ hơn 0.8. Những thay đổi về hình dạng kênh, độ dốc, hướng chảy và độ nhám sẽ ảnh hưởng đến dòng chảy trong một khoảng cách ngắn phía thượng lưu. Việc kiểm soát trong dòng chảy dưới tới hạn là ở phía hạ lưu. Dòng chảy dưới tới hạn phổ biến ở các kênh, máng và suối nằm ở vùng đồng bằng và thung lũng có độ dốc tương đối bằng phẳng.
Độ sâu tới hạn là quan trọng trong phân tích thủy lực vì nó luôn là điểm kiểm soát thủy lực. Dòng chảy phải đi qua độ sâu tới hạn khi chuyển từ dòng chảy dưới tới hạn sang dòng chảy siêu tới hạn hoặc ngược lại. Trong trường hợp thứ hai, thường xảy ra bước nhảy thủy lực. Các vị trí điển hình của độ sâu tới hạn gồm:
- Tại những thay đổi đột ngột về độ dốc khi một độ dốc phẳng (dưới tới hạn) chuyển nhanh sang độ dốc lớn (siêu tới hạn).
- Tại các điểm thắt trong kênh như miệng cống, chuyển tiếp máng đo, v.v. trong một số điều kiện.
- Tại cửa ra không bị ngập của cống hoặc máng đo trên độ dốc dưới tới hạn, chảy ra một kênh rộng có độ dốc lớn (siêu tới hạn), hoặc rơi tự do ở cửa ra.
- Tại đỉnh của đập tràn, đập tràn tràn hoặc đê.
- Tại các điểm thắt hẹp cầu nơi dòng chảy bị nghẽn.
Vị trí và độ lớn của độ sâu tới hạn cũng như việc xác định độ dốc tới hạn cho một mặt cắt có hình dạng, kích thước và độ nhám nhất định là quan trọng trong thiết kế và phân tích thủy lực. Các phương trình để xác định độ sâu tới hạn được trình bày trong phần thảo luận về lưu lượng riêng và năng lượng riêng trong dòng chảy không đều ổn định (Xem Mục 4.6).
(nd: phân loại dòng chảy theo số Froude)
Phân loại dòng chảy theo số Froude
Fr=1.0 → Dòng chảy tới hạn (critical flow).
Fr>1.0 → Dòng chảy siêu tới hạn (supercritical flow) hoặc dòng chảy nhanh.
Fr<1.0 → Dòng chảy dưới tới hạn (subcritical flow) hoặc dòng chảy êm.
Đặc điểm dòng siêu tới hạn Fr>1:
- Khó kiểm soát, vì thay đổi đột ngột trong hình dạng hoặc hướng dòng chảy có thể tạo ra sóng truyền xuống hạ lưu, làm nước tràn qua bờ kênh.
- Thay đổi về hình dạng kênh, độ dốc, hướng dòng chảy hoặc độ nhám không ảnh hưởng đến dòng chảy ở thượng lưu.
- Dòng chảy được kiểm soát ở thượng lưu.
- Thường xảy ra ở kênh có độ dốc lớn, như máng dốc, kênh núi, hoặc các công trình điều tiết nước có dòng chảy nhanh.
Đặc điểm dòng dưới tới hạn Fr<1:
- Dễ kiểm soát hơn, đặc biệt nếu Fr<0.8.
- Thay đổi về hình dạng kênh, độ dốc, hướng dòng chảy hoặc độ nhám có thể ảnh hưởng đến dòng chảy ở một khoảng cách nhất định về phía thượng lưu.
- Dòng chảy được kiểm soát ở hạ lưu.
- Thường gặp ở kênh bằng phẳng, sông vùng đồng bằng hoặc thung lũng có độ dốc nhỏ.
Nhảy thủy lực: Hiện tượng chuyển từ dòng chảy siêu tới hạn sang dòng chảy dưới tới hạn thường xảy ra đột ngột (đặc biệt khi Fr>2..0), dẫn đến hiện tượng gọi là “nhảy thủy lực” (hydraulic jump).
Độ sâu tới hạn là quan trọng trong phân tích thủy lực vì nó luôn là điểm kiểm soát thủy lực. Dòng chảy phải đi qua độ sâu tới hạn khi chuyển từ dòng chảy dưới tới hạn sang dòng chảy siêu tới hạn hoặc ngược lại. Trong trường hợp thứ hai, thường xảy ra bước nhảy thủy lực.
4.4 Dòng chảy không ổn định
Các loại dòng chảy không ổn định mà kỹ sư thoát nước đường giao thông quan tâm bao gồm:
- Sóng do gió và tàu thuyền gây ra khi làm xáo trộn mặt nước.
- Sóng do mất ổn định bề mặt nước, xảy ra khi dòng chảy có số Froude xấp xỉ 1.0.
- Sóng do nhiễu loạn dòng chảy, xảy ra khi có sự thay đổi hướng dòng chảy và số Froude lớn hơn khoảng 2.0.
- Sóng dâng hoặc sóng triều, xuất hiện khi có sự thay đổi đột ngột về lưu lượng dòng chảy, ví dụ như khi mở hoặc đóng cửa cống, hoặc chuyển động của thủy triều trong các dòng sông ven biển.
- Sóng đứng và sóng ngược dòng (antidunes), xuất hiện trong dòng chảy phù sa.
- Sóng lũ, hình thành do sự di chuyển dần xuống hạ lưu của dòng chảy lũ hoặc sự xả nước từ hồ chứa.
Sóng là yếu tố quan trọng trong thiết kế thủy lực cầu, đặc biệt khi thiết kế bảo vệ mái dốc nền đường, đê kè, và cải tạo kênh.
Trong các phần sau, sẽ chỉ trình bày phân tích cơ bản một chiều về sóng và sóng xung kích. Các khía cạnh khác của sóng sẽ được đề cập ở các mục khác.
4.4.1 Sóng trọng lực
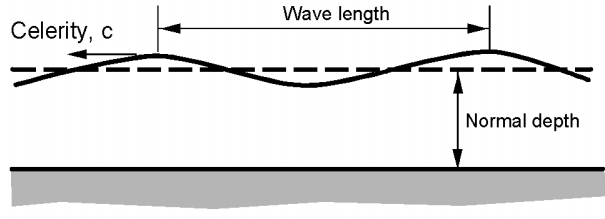
Đối với sóng nước nông (sóng dài – Hình 4.5), khi normal depth (yo) nhỏ so với bước sóng, phương trình cơ bản cho tốc độ truyền sóng (celerity – vận tốc của sóng so với vận tốc dòng chảy) được cho bởi:
$$c = \sqrt{g y_o} \tag{4.17}$$
Lưu ý rằng tốc độ truyền sóng của một sóng nước nông biên độ nhỏ chính là mẫu số của Số Froude.
$$Fr = \frac{V}{\sqrt{g y_o}} \tag{4.18}$$
Như đã giải thích trong phần thảo luận về Số Froude (Mục 4.3.5), khi Fr<1 (dưới tới hạn hoặc yên tĩnh), một sóng biên độ nhỏ di chuyển ngược dòng. Khi Fr>1 (dòng chảy siêu tới hạn hoặc nhanh), một sóng biên độ nhỏ di chuyển xuôi dòng và khi Fr=1 (dòng chảy tới hạn), sóng biên độ nhỏ đứng yên. Thực tế rằng sóng hoặc đợt sóng không thể di chuyển ngược dòng khi Số Froude bằng hoặc lớn hơn 1.0 là điều quan trọng cần ghi nhớ khi xác định thời điểm mối quan hệ giữa mực nước và lưu lượng tại một mặt cắt có thể bị ảnh hưởng bởi điều kiện hạ lưu.
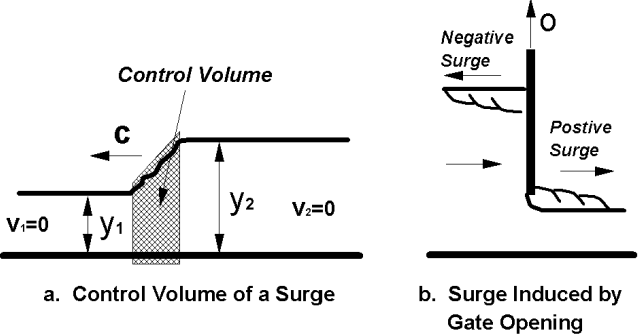
4.4.2 Sóng dâng (Surges)
Một đợt sóng dâng (surge) là sự gia tăng nhanh chóng của độ sâu dòng chảy (Hình 4.6). Sóng dâng có thể xảy ra do việc xả nước đột ngột từ một con đập hoặc do thủy triều dâng. Việc nâng một cánh cửa trong kênh không chỉ tạo ra một sóng dâng dương di chuyển xuôi dòng, mà còn tạo ra một sóng dâng âm di chuyển ngược dòng (Hình 4.6). Khi di chuyển ngược dòng, sóng dâng âm sẽ nhanh chóng bị dàn phẳng. Xem HDS 6 để biết thêm chi tiết và phương trình cơ bản của sóng dâng (Richardson et al. 2001).
.
4.5 Dòng chảy ổn định không đều
Dòng chảy ổn định không đều xảy ra khi lưu lượng nước (Q) không đổi, nhưng độ sâu dòng chảy, vận tốc hoặc tiết diện dòng chảy thay đổi từ mặt cắt này sang mặt cắt khác. Theo phương trình liên tục, mối quan hệ giữa các mặt cắt sẽ là:
Q = A₁V₁ = A₂V₂ = … = AₙVₙ (4.19)
Vận tốc trong dòng chảy ổn định không đều có thể được tính bằng phương trình Manning nếu sự thay đổi vận tốc giữa các mặt cắt là nhỏ, sao cho hiệu ứng gia tốc không đáng kể.
Kỹ sư thủy lực cần hiểu rõ dòng chảy không đều để xác định hành vi của dòng nước khi có sự thay đổi về sức cản dòng chảy, kích thước, tiết diện, hình dạng hoặc độ dốc của kênh.
Ví dụ điển hình có thể bao gồm việc xác định thay đổi cao độ mặt nước trong một kênh có độ dốc không đổi khi nó chuyển tiếp trong thời gian ngắn từ một tiết diện hình thang bê tông (với hệ số Manning nhỏ) sang tiết diện hình thang có lót cỏ (với hệ số Manning lớn), hoặc một con suối có độ dốc và hệ số Manning không đổi nhưng có một cống làm thu hẹp dòng chảy.
Hai tình huống này xác định hai trường hợp cơ bản của dòng chảy ổn định không đều:
- Trường hợp thứ nhất là đối với khoảng cách tương đối ngắn (từ vài mét (feet) đến vài trăm mét (feet)), nơi mà gia tốc đóng vai trò quan trọng hơn ma sát. Trường hợp này được gọi là DÒNG CHẢY ỔN ĐỊNH THAY ĐỔI NHANH (Steady Rapidly Varied Flow). Tác động của ma sát, nếu quan trọng, sẽ được tính đến bằng cách chia đoạn dòng chảy thành các đoạn ngắn hơn và áp dụng phương trình Manning trên từng đoạn ngắn đó.
- Trường hợp thứ hai là đối với khoảng cách dài (hàng trăm đến hàng ngàn mét (feet)), nơi mà tổn thất do ma sát quan trọng hơn gia tốc. Trường hợp này được gọi là DÒNG CHẢY THAY ĐỔI CHẬM (Gradually Varied Flow).
Phương pháp phân tích và các phương trình cho hai trường hợp này sẽ được trình bày trong hai phần tiếp theo.
4.6 Dòng chảy Ổn Định Thay Đổi Nhanh (Steady Rapidly Varied Flow)
4.6.1 Giới thiệu
Dòng chảy ổn định qua các đoạn chuyển tiếp ngắn, nơi dòng chảy là đều trước và sau chuyển tiếp, có thể được phân tích bằng phương trình năng lượng. Tổn thất năng lượng do ma sát có thể được bỏ qua, ít nhất là trong bước xấp xỉ đầu tiên. Phân tích có thể được tinh chỉnh thêm trong bước thứ hai bằng cách tính đến tổn thất ma sát.
Ví dụ, cao độ mặt nước qua đoạn chuyển tiếp được xác định bằng phương trình năng lượng, sau đó được hiệu chỉnh bằng cách tính đến ảnh hưởng của tổn thất ma sát lên vận tốc và độ sâu trong các đoạn nhỏ qua vùng chuyển tiếp. Tuy nhiên, tổn thất năng lượng do hiện tượng tách dòng không thể bỏ qua, và các đoạn chuyển tiếp có nguy cơ xảy ra tách dòng cần được xử lý đặc biệt, có thể bao gồm cả mô hình vật lý. Dòng hội tụ (các dòng chảy hội tụ lại) ít bị tách dòng hơn so với dòng phân tán.
Ngoài ra, bất kỳ khi nào một đoạn chuyển tiếp gây ra sự thay đổi vận tốc và độ sâu sao cho số Froude tiến gần đến 1, các vấn đề như sóng, tắc nghẽn hoặc nghẹt dòng có thể xảy ra. Nếu dòng chảy đến là siêu tới hạn (supercritical), có thể xảy ra bước nhảy thủy lực (hydraulic jump). Các đoạn chuyển tiếp đối với dòng siêu tới hạn sẽ được bàn đến trong phần tiếp theo.
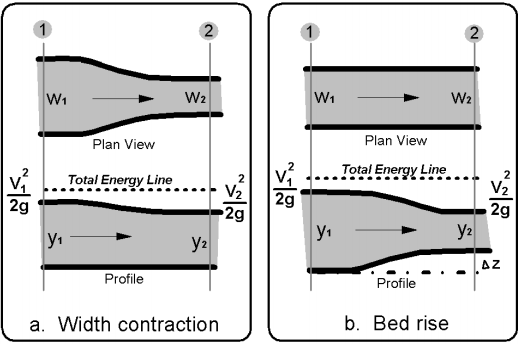
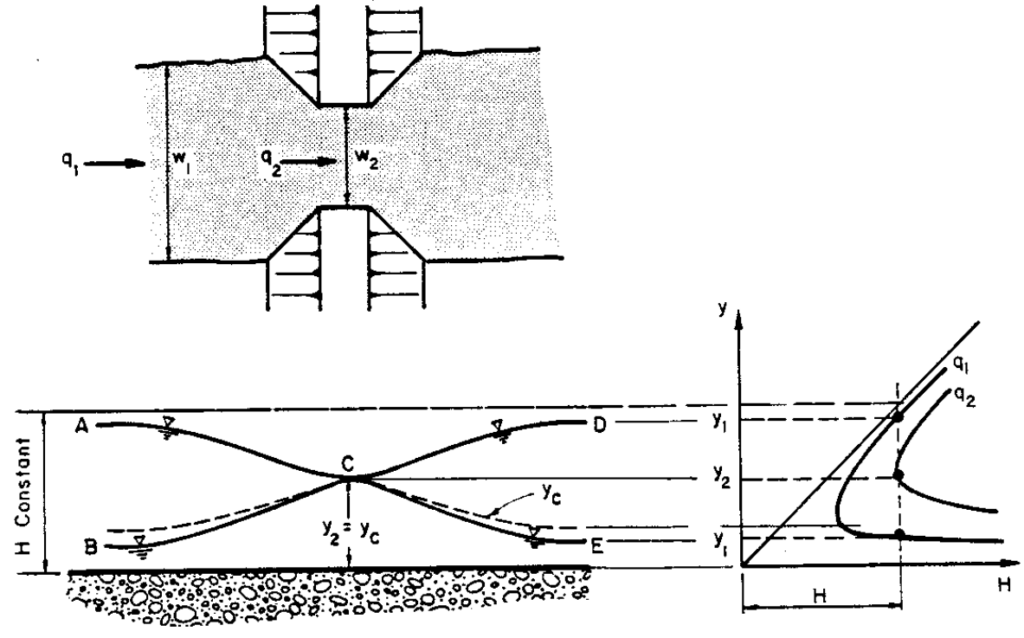
Các đoạn chuyển tiếp được sử dụng để thu hẹp hoặc mở rộng bề rộng kênh (Hình 4.7a), để nâng hoặc hạ cao trình đáy kênh (Hình 4.7b), hoặc để thay đổi cả bề rộng và cao trình đáy. Việc phân tích hoặc thiết kế đoạn chuyển tiếp được hỗ trợ bởi việc sử dụng các đại lượng độ sâu và cột áp vận tốc trong phương trình năng lượng (xem Chương 3). Tổng của hai thành phần này được gọi là năng lượng riêng (specific energy) hoặc cột áp riêng (specific head), ký hiệu là H, được định nghĩa như sau:
$$H = \frac{V^2}{2g} + y = \frac{q^2}{2gy^2} + y \tag{4.20}$$
Trong đó:
- H – Năng lượng riêng, m (hoặc ft)
- V – Vận tốc, m/s (ft/s)
- q – Lưu lượng đơn vị, được định nghĩa là lưu lượng chia theo bề rộng (m³/s/m hay ft³/s/ft) trong kênh hình chữ nhật
- g – Gia tốc trọng trường, 9.81 m/s² (32.2 ft/s²)
- y – Độ sâu dòng chảy, m (hoặc ft)
Năng lượng riêng H là chiều cao của tổng năng lượng tính từ đáy kênh.
Mối quan hệ giữa ba đại lượng trong phương trình năng lượng riêng — q, y và H — được đánh giá bằng cách:
- Giữ q không đổi → xác định mối quan hệ giữa H và y → cho ra biểu đồ cột áp riêng (specific energy diagram).
- Giữ H không đổi → xác định mối quan hệ giữa q và y → cho ra biểu đồ lưu lượng riêng (specific discharge diagram).
Các biểu đồ này tương ứng với một lưu lượng hoặc năng lượng cho trước, được sử dụng để phân tích hoặc thiết kế các đoạn chuyển tiếp, hoặc khi dòng chảy đi qua cầu. Chúng sẽ được trình bày trong hai phần tiếp theo.
4.6.2 Biểu đồ năng lượng riêng và xác định độ sâu tới hạn
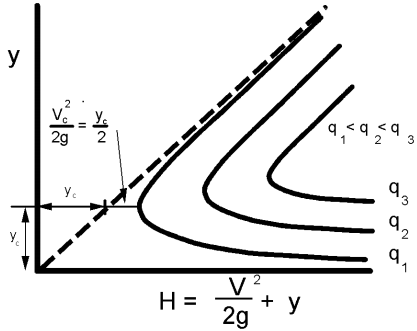
Đối với một giá trị q cho trước, Phương trình 4.20 có thể được giải với nhiều giá trị H và y khác nhau. Khi y được biểu diễn dưới dạng hàm của H, sẽ thu được Hình 4.8. Có hai độ sâu khả dĩ, ứng với mỗi giá trị H lớn hơn một giá trị tối thiểu xác định. Do đó, với năng lượng riêng lớn hơn giá trị tối thiểu, dòng chảy có thể có độ sâu lớn với vận tốc nhỏ, hoặc độ sâu nhỏ với vận tốc lớn. Dòng chảy ứng với một lưu lượng đơn vị q không thể xảy ra nếu năng lượng riêng nhỏ hơn giá trị tối thiểu.
Một độ sâu duy nhất của dòng chảy tại mức năng lượng tối thiểu được gọi là độ sâu tới hạn, ký hiệu là yₐ, và vận tốc tương ứng, gọi là vận tốc tới hạn, ký hiệu là Vc = q / yc. Mối quan hệ giữa yc và Vc đối với một giá trị q cho trước (trong kênh hình chữ nhật) là:
$$y_c = \left(\frac{q^2}{g}\right)^{1/3} = \frac{2 V_c^2}{2g} \tag{4.21}$$
Lưu ý rằng đối với dòng tới hạn: $$\frac{V_c}{\sqrt{g y_c}} = 1 = Fr \tag{4.22}$$
Và: $$H_{\text{min}} = \frac{V_c^2}{2g} + y_c = \frac{3}{2} y_c \tag{4.23}$$
Do đó, dòng chảy tại năng lượng riêng tối thiểu có số Froude bằng 1. Dòng chảy có vận tốc lớn hơn vận tốc tới hạn (Fr > 1) được gọi là dòng chảy nhanh hoặc siêu tới hạn (supercritical), còn dòng chảy có vận tốc nhỏ hơn vận tốc tới hạn (Fr < 1) được gọi là dòng chảy chậm hoặc dưới tới hạn (subcritical). Các trạng thái dòng chảy này được minh họa trong Hình 4.9, nơi mà một chỗ nâng cao đáy kênh sẽ gây ra giảm độ sâu dòng chảy khi dòng chảy là chậm, và tăng độ sâu dòng chảy khi dòng chảy là nhanh.
Hơn nữa, tồn tại một mức nâng đáy lớn nhất tương ứng với một giá trị H₁ cho trước, tại đó lưu lượng dòng chảy được giữ không đổi một cách vật lý. Nếu phần nâng đáy vượt quá Δzₘₐₓ ứng với Hₘᵢₙ, thì độ sâu dòng chảy đến (y₁) sẽ phải tăng lên (tức là tăng H), hoặc lưu lượng dòng chảy sẽ phải giảm xuống.
Do đó, đối với một dòng chảy nhất định trong kênh, mức nâng đáy có thể xảy ra tối đa là Δzₘₐₓ mà không gây ra hiện tượng nước ngược (backwater effect).
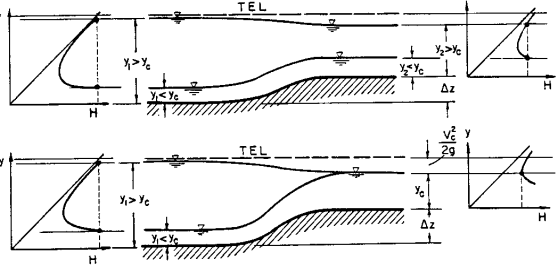
(nd: backwater)
Backwater Effect là hiện tượng mực nước dâng lên ở thượng lưu do bị cản trở ở hạ lưu, ảnh hưởng lớn đến thiết kế thủy lực kênh, cống, cầu, và kiểm soát lũ.
Phân biệt các loại dòng chảy và cách mà mặt nước phản ứng khi thay đổi tiết diện dòng chảy là điều quan trọng trong thiết kế kênh; do đó, việc xác định vị trí của độ sâu tới hạn và độ dốc tới hạn của một tiết diện với hình dạng, kích thước và độ nhám cho trước là cần thiết. Các phương trình để giải trực tiếp độ sâu tới hạn có sẵn cho một số hình dạng lăng trụ điển hình (Brater và King 1976); tuy nhiên, một số phương trình này không được thiết lập cho hệ đơn vị mét.
Với bất kỳ tiết diện kênh nào, đều hay không đều, độ sâu tới hạn có thể được tìm bằng phương pháp thử-sai từ phương trình sau:
$$\frac{A_c^3}{T_c} = \frac{Q^2}{g} \tag{4.24}$$
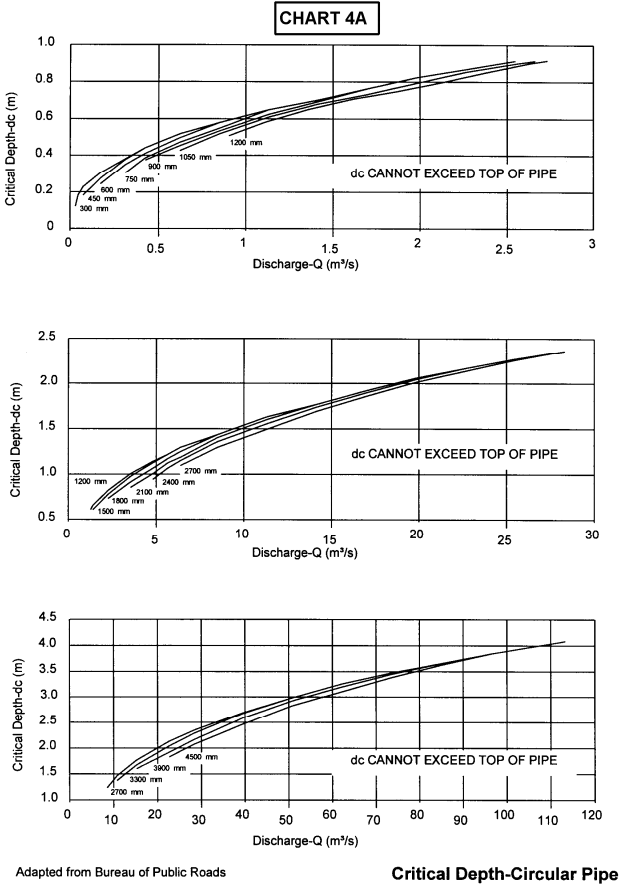
trong đó Ac và Tc lần lượt là diện tích và bề rộng mặt nước tại dòng chảy tới hạn. Các toán đồ (nomograph) có sẵn để giải phương trình này, đặc biệt hữu ích cho các tiết diện hình tròn (Hình 4.10a và b). Biểu thức tính vận tốc tới hạn Vc cho bất kỳ tiết diện nào tại điều kiện dòng chảy tới hạn là:
$$V_c = \sqrt{g y_c} \tag{4.25}$$
Trong đó:
$$y_c = \frac{A_c}{T_c} \tag{4.26}$$
(nd: tính độ sâu tới hạn online)
+ độ sâu tới hạn trong kênh online
+ độ sâu tới hạn trong cống online
Dòng chảy đều trong phạm vi khoảng 10% quanh độ sâu tới hạn là không ổn định và nên tránh trong thiết kế. Lý do dòng chảy không ổn định có thể được thấy khi tham chiếu biểu đồ cột áp riêng (Hình 4.8).
Khi dòng chảy tiến gần đến độ sâu tới hạn từ một trong hai phía của đường cong, chỉ cần một thay đổi nhỏ về năng lượng cũng đủ làm độ sâu thay đổi đột ngột sang độ sâu thay thế nằm ở phía đối diện của đường cong cột áp riêng. Nếu vùng dòng chảy không ổn định không thể tránh được trong thiết kế, thì nên giả định loại dòng chảy có điều kiện bất lợi nhất để dùng trong thiết kế.
(nd: dòng chảy rơi vào vùng bất ổn định)
Nếu trong thiết kế không thể tránh khỏi việc dòng chảy rơi vào vùng không ổn định (tức là vùng gần độ sâu tới hạn, thường ±10% quanh yc), thì phải giả định loại dòng chảy có điều kiện bất lợi nhất để dùng trong thiết kế vì:
- Khi dòng chảy ở gần độ sâu tới hạn, chỉ một thay đổi nhỏ về năng lượng (ví dụ do địa hình đáy thay đổi nhẹ) có thể làm độ sâu nhảy đột ngột sang một giá trị khác ở “nhánh đối diện” trên đường cong năng lượng riêng.
- Ví dụ: Dòng chảy siêu tới hạn (nhỏ, nhanh) có thể chuyển sang chậm và sâu hơn — gây ngập, hoặc ngược lại gây xói
Nói các khác: Nếu không chắc dòng là loại nào (và không thể tránh được vùng không ổn định), thì nên giả định loại gây hại hơn:
- Nếu lo sợ xói → giả định dòng là siêu tới hạn để tính toán kết cấu chắc chắn hơn.
- Nếu lo ngập → giả định dòng là dưới tới hạn để đảm bảo thoát nước.
4.6.3 Biểu đồ lưu lượng riêng
Phương trình 4.20 có thể được biến đổi lại để xác định q, tức là lưu lượng đơn vị, dưới dạng hàm của H (năng lượng riêng) và y (độ sâu dòng chảy):
$$q = y \sqrt{2g(H – y)} \tag{4.27}$$
Với một giá trị H không đổi, q có thể được giải dưới dạng hàm theo y, và kết quả sẽ tạo ra biểu đồ lưu lượng riêng (specific discharge diagram) (Hình 4.11).
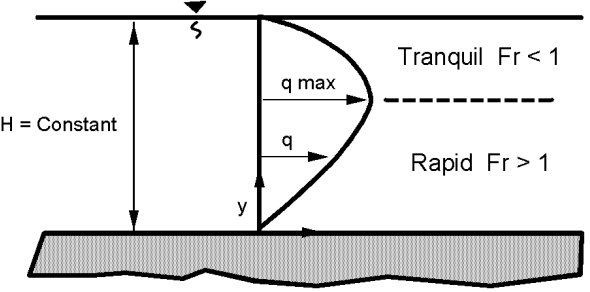
Hình 4.11. Biểu đồ lưu lượng riêng (specific discharge diagram).
Đối với bất kỳ lưu lượng nào nhỏ hơn một giá trị cực đại cụ thể q ứng với giá trị H cho trước, sẽ tồn tại hai độ sâu dòng chảy khả dĩ.
Độ sâu tại lưu lượng cực đại q với một năng lượng riêng H cho trước được gọi là độ sâu tới hạn (yc), và vận tốc tương ứng là vận tốc tới hạn (Vc).
$$y_c = \frac{2}{3}H = 2 \cdot \frac{V_c^2}{2g} \tag{4.28}$$
Và:
$$\frac{V_c}{\sqrt{g y_c}} = 1 = Fr \tag{4.29}$$
Trong đó:
- yc: độ sâu tới hạn
- Vc: vận tốc tới hạn
- Fr: số Froude = 1 tại dòng chảy tới hạn
Ví dụ 4.5 – Tính độ sâu và vận tốc tới hạn
Cho: Xác định độ sâu tới hạn trong một rãnh hình thang với:
- Hệ số mái dốc: z=1 (tức là 1H:1V)
- Lưu lượng dòng chảy: Q = 9.2 m³/s
- Chiều rộng đáy: B = 6 m
Hỏi: Độ sâu tới hạn, vận tốc tới hạn.
Giải:
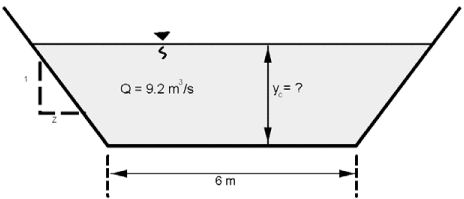
Với Q=9.2 m3/s, áp dụng phương trình xác định độ sâu tới hạn:
$$\frac{A_c^3}{T_c}=\frac{Q^2}g$$
$$\frac{A_c^3}{T_c}=\frac{9.2^2}{9.81}=8.63$$
Đối với kênh hình thang, sử dụng các công thức:
- Diện tích mặt cắt ngang: A = y (B + Zy)
- Bề rộng mặt nước: T = B + 2Zy
Thay vào phương trình: $$8.63=\frac{[y(6+y)]^3}{(6+2y)}$$
Giải bằng phương pháp thử-sai, ta tìm được: y=0.6 m
$$y_c=\frac{A}{T} = \frac{0.6 (6 + 0.6)}{(6 + 1.2)} = 0.55 \, m$$
$$V_c = \sqrt{g y_c} = \sqrt{9.81 \times 0.55} = 2.3 \, m/s$$
Đối với lưu lượng cực đại tại H không đổi, số Froude bằng 1.0, và dòng chảy ở trạng thái tới hạn. Mối quan hệ giữa yc, Vc, H và qmax khi H không đổi là:
$$y_c = \frac{2}{3} H = 3 \sqrt{\frac{q_{\text{max}}^2}{g}} = \frac{2 V_c^2}{2g} \tag{4.30}$$
Các điều kiện dòng chảy với năng lượng riêng không đổi trong trường hợp thu hẹp bề rộng được minh họa trong Hình 4.12, giả sử không có ảnh hưởng hình học như lệch tâm, lệch dòng, trụ cầu hay đoạn mở rộng.
Thu hẹp dòng sẽ làm giảm độ sâu dòng chảy khi dòng chảy là chậm (tranquil) và tăng độ sâu khi dòng là nhanh (rapid). Mức thu hẹp lớn nhất mà không gây backwater xảy ra khi số Froude bằng 1.0, lưu lượng đơn vị đạt cực đại, và \(y_c = \frac{2}{3} H\). Nếu thu hẹp thêm, sẽ gây backwater — tức là dòng thượng lưu phải tăng độ sâu để tạo ra năng lượng riêng lớn hơn nhằm duy trì dòng qua tiết diện bị thu hẹp.
Dòng chảy trong Hình 4.12 có thể đi từ điểm A đến C, sau đó hoặc quay lại D hoặc đi xuống E tùy thuộc vào điều kiện biên phía hạ lưu. Nếu đáy kênh phía hạ lưu điểm C có độ dốc tăng và không xảy ra tách dòng, thì dòng có thể đi theo đường A → C → E. Tương tự, dòng có thể đi từ B → C rồi đến E hoặc đi lên D, tùy vào điều kiện biên.
Hình 4.12 được vẽ với ranh giới bên là dòng mượt (streamline). Nếu thu hẹp là do trụ cầu, dòng thượng lưu sẽ theo đường dòng tự nhiên đến điểm thắt hẹp nhất, nhưng sau đó dòng có khả năng sẽ bị tách (separation). Dòng chảy tiếp cận ở trạng thái tranquil có thể đi theo A → C, nhưng dòng ở hạ lưu có thể không đi tiếp qua C → D hoặc C → E, mà thay vào đó xuất hiện một hydraulic jump gợn sóng.
Sẽ có sự tương tác dòng chảy trong vùng tách dòng và tổn thất năng lượng đáng kể. Nếu độ dốc phía hạ lưu của trụ cầu bằng với độ dốc phía thượng lưu, dòng chảy không thể được duy trì với mức năng lượng đó. Backwater sẽ xảy ra, làm tăng độ sâu (nd: nước dâng) tại vị trí thắt hẹp và phía thượng lưu, cho đến khi dòng có thể đi qua chỗ thu hẹp và ổn định lại phía hạ lưu.
(nd: nhảy thủy lực gợn sóng)
Nhảy thủy lực gợn sóng (undulating hydraulic jump) là một dạng đặc biệt của hiện tượng nhảy thủy lực, trong đó thay vì có một bước nhảy đột ngột về độ sâu như trong nhảy thủy lực thông thường, quá trình chuyển tiếp từ dòng chảy nhanh sang dòng chảy chậm diễn ra một cách từ từ và liên tục, tạo thành các sóng gợn trên bề mặt nước.
Đặc điểm của nhảy thủy lực gợn sóng:
- Sự thay đổi độ sâu dần dần: Không có một bước nhảy đột ngột như trong nhảy thủy lực thông thường mà độ sâu tăng dần theo một khoảng cách nhất định.
- Sóng gợn trên bề mặt nước: Xuất hiện các sóng gợn sóng trên bề mặt nước trong vùng nhảy thủy lực.
- Năng lượng tiêu tán dần: Năng lượng của dòng chảy bị tiêu tán dần trong quá trình chuyển tiếp, không tập trung vào một điểm như trong nhảy thủy lực thông thường.
- Xảy ra trong điều kiện dòng chảy nhất định: Nhảy thủy lực gợn sóng thường xảy ra khi độ dốc của kênh giảm dần và lưu lượng nước không quá lớn.
Nguyên nhân hình thành:
Sự cản trở của các vật thể: Sự có mặt của các vật thể như trụ cầu, mố cầu hoặc các thay đổi đột ngột về hình dạng của kênh cũng có thể gây ra sự hình thành nhảy thủy lực gợn sóng.
Sự thay đổi độ dốc của đáy kênh: Khi độ dốc của đáy kênh giảm dần, dòng chảy sẽ dần mất đi năng lượng và chuyển sang trạng thái ổn định mới với độ sâu lớn hơn. Quá trình chuyển tiếp này tạo ra các sóng gợn.
4.6.4. Nhảy thủy lực
Nhảy thủy lực sẽ xảy ra khi vận tốc dòng chảy (V1) nhanh hoặc siêu tới hạn, và độ dốc giảm xuống mức phù hợp cho dòng chảy dưới tới hạn, hoặc có một vật cản như bộ phận tiêu năng được đặt trong dòng chảy. Độ sâu siêu tới hạn sẽ chuyển thành độ sâu dưới tới hạn, được gọi là độ sâu sequent. Tùy thuộc vào độ lớn của số Froude, một lượng năng lượng đáng kể sẽ chuyển thành nhiệt. Số Froude càng lớn, tổn thất năng lượng càng cao.
Sự tồn tại của một cú nhảy thủy lực giả định rằng có đủ điều kiện nước hạ lưu (tailwater) để duy trì độ sâu sequent.
(nd: sequent depth)
Nhảy thủy lực xảy ra khi:
– Tốc độ dòng chảy ban đầu (ký hiệu là V1) rất lớn (dòng siêu tới hạn – supercritical flow).
– Sau đó, dòng chảy gặp một đoạn dốc thoải hơn, hoặc gặp vật cản làm giảm năng lượng (energy dissipator), khiến dòng chảy chuyển sang dưới tới hạn (subcritical).
– Khi đó, độ sâu nước thay đổi đột ngột: từ độ sâu ban đầu y1 (nông) → độ sâu sau nhảy y2 (sâu). Độ sâu y2 chính là sequent depth.
– Trong quá trình này, năng lượng bị mất đi (do chuyển sang nhiệt hoặc nhiễu loạn), phụ thuộc vào số Froude Fr1
Nhiều kỹ sư/nhà thiết kế giả định rằng nhảy thủy lực sẽ luôn xảy ra khi có sự thay đổi từ độ dốc lớn sang độ dốc nhỏ, chẳng hạn như ở cuối cửa ra của cống gãy khúc (broken-back culvert). Tuy nhiên, nhảy thủy lực chỉ xảy ra khi có đủ mực nước hạ lưu để duy trì độ sâu sequent ngay bên dưới điểm gãy độ dốc của cống. Nếu không có đủ nước hạ lưu, cú nhảy sẽ bị đẩy xuống hạ lưu khỏi cống, gây ra một hố xói lớn tiềm tàng tại cửa ra của cống.
Mối quan hệ giữa độ sâu siêu tới hạn-y1 và độ sâu sequent-y2 đối với kênh chữ nhật đáy phẳng được xác định theo công thức:
$$\frac{y_2}{y_1} = \frac{1}{2} \left[ \left(1 + 8 \, Fr_1^2 \right)^{1/2} – 1 \right] \tag{4.31}$$
Tổn thất năng lượng tương ứng trong một hiện tượng nhảy thủy lực (hydraulic jump) là chênh lệch giữa hai mức năng lượng riêng. Có thể chứng minh rằng tổn thất cột nước này được tính theo:
$$\Delta H = h_L = \frac{(y_2 – y_1)^3}{4 y_1 y_2} \tag{4.32}$$
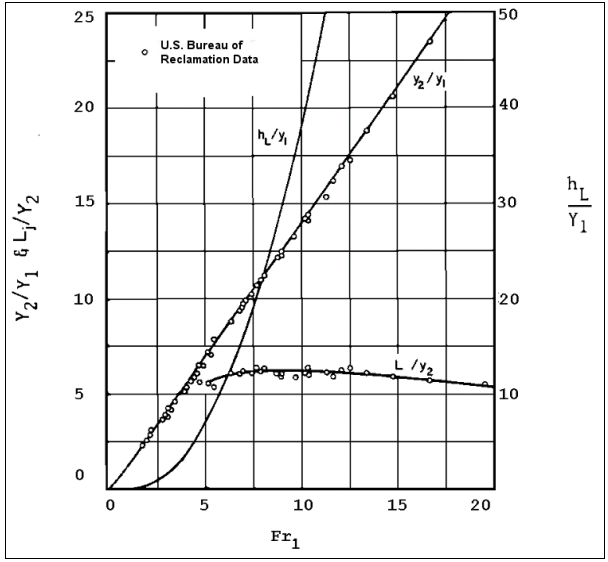
Phương trình 4.32 đã được xác minh thực nghiệm cùng với sự phụ thuộc của chiều dài cú nhảy (Lj) và sự tiêu tán năng lượng (tổn thất cột nước hL) vào Số Froude của dòng chảy tiếp cận (Fr1). Kết quả của các thí nghiệm này được trình bày trong Hình 4.13.
Khi Số Froude của dòng chảy nhanh nhỏ hơn 2.0, cú nhảy dao động với các sóng bề mặt lớn sẽ được tạo ra. Các sóng này sẽ lan truyền một khoảng cách đáng kể về phía hạ lưu.
Ngoài ra, khi Số Froude của dòng chảy tiếp cận nhỏ hơn 3.0, sự tiêu tán năng lượng của cú nhảy không lớn và các tia dòng chảy có vận tốc cao có thể tồn tại một khoảng cách nhất định về phía hạ lưu của cú nhảy. Những sóng và tia nước này có thể gây xói mòn đáng kể ở hạ lưu.
Đối với các giá trị Số Froude lớn hơn, tốc độ tiêu tán năng lượng trong cú nhảy là rất lớn, và Hình 4.13 được khuyến nghị sử dụng.
Ví dụ 4.6 – Xác đinh cú nhảy thủy lực
Cho: Một cú nhảy thủy lực xảy ra trong một kênh chữ nhật rộng 5 m tại độ sâu dòng chảy 0,5 m.
Xác định mực nước hạ lưu cần thiết để gây ra cú nhảy. Đồng thời, tính tổn thất cột nước do cú nhảy. Biết Q = 20 m³/s.
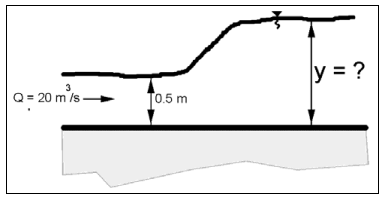
Hỏi:
(1) Xác định mực nước hạ lưu cần thiết (WSEL) để gây ra cú nhảy.
(2) Xác định tổn thất cột nước qua cú nhảy.
Giải:
(1) Sử dụng công thức cho nhảy thủy lực (Phương trình 4.31) để tìm y2:
Từ phương trình liên tục:
$$V_1 = \frac{Q}{A_1} = \frac{20}{5 \cdot 0.5} = 8 \, \text{m/s}$$
Tính số Froude:
$$Fr = \frac{V_1}{\sqrt{g y_1}} = \frac{8}{\sqrt{9.81 \cdot 0.5}} = 3.6$$
Áp dụng phương trình 4.31:
$$y_2 = \frac{y_1}{2} \left[ \left(1 + 8 \cdot Fr_1^2 \right)^{1/2} – 1 \right]$$
$$y_2 = \frac{0.5}{2} \left[ \left(1 + 8 \cdot 3.6^2 \right)^{1/2} – 1 \right] = 2.3 \, \text{m}$$
(2) Tính tổn thất cột nước hL qua nhảy thủy lực (Phương trình 4.32):
$$h_L = \frac{(y_2 – y_1)^3}{4 y_1 y_2}$$
$$h_L = \frac{(2.3 – 0.5)^3}{4 \cdot 2.3 \cdot 0.5} = 1.27 \, \text{m}$$
4.6.5 Dòng chảy dưới tới hạn trong khúc cua
Khi dòng chảy dưới tới hạn đi qua một khúc cua, mực nước sẽ dâng cao ở phía ngoài khúc cua và hạ thấp ở phía trong khúc cua (Hình 4.14). Sự chênh lệch xấp xỉ về độ cao mực nước (ΔZ) giữa hai bên của kênh cong có thể được xác định bằng các phương trình sau.
$$\Delta Z = Z_o – Z_i = \frac{V^2}{g r_c} (r_o – r_i) \tag{4.33}$$
trong đó:
- Z = Cao độ mặt nước, m (ft)
- V = Vận tốc trung bình trong kênh, m/s (ft/s)
- g = Gia tốc trọng trường, 9.81 m/s² (32.2 ft/s²)
- rc = Bán kính cong tới tim của kênh, m (ft)
- r₀ = Bán kính cong tới dòng chảy phía ngoài khúc cong, m (ft)
- rᵢ = Bán kính cong tới dòng chảy phía trong khúc cong, m (ft)
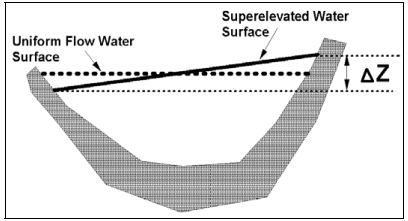
Trong thiết kế kênh, sự nâng cao mặt nước (superelevation) được tính bằng cách cộng ΔZ/2 vào độ sâu normal để xác định mực nước tối đa ở phía ngoài của khúc cua.
Phương trình này cho giá trị ΔZ thấp hơn một chút so với thực tế trong các kênh tự nhiên do giả định vận tốc đồng đều và độ cong đồng đều. Tuy nhiên, sai số của giá trị tính toán thường dưới 10%. Phương trình 4.34 (HDS 6, Richardson et al., 2001) chính xác hơn, nhưng sự khác biệt về superelevation giữa hai phương trình là nhỏ. Trong các kênh phù sa, hiện tượng xói lở bờ lõm và bồi tụ ở bờ lồi còn làm tăng thêm sai số trong việc tính toán sự nâng cao mặt nước.
$$\Delta Z = \frac{V_{\text{max}}^2}{2g} \left\{ 2 – \left( \frac{r_i}{r_c} \right)^2 – \left( \frac{r_c}{r_o} \right)^2 \right\} \tag{4.34}$$
trong đó
- ri: bán kính dòng chảy phía trong khúc cong
- rc: bán kính tới tim kênh
- ro: bán kính dòng chảy phía ngoài khúc cong
Khuyến nghị sử dụng Phương trình 4.33 để tính toán sự nâng cao mặt nước (superelevation) trong các kênh phù sa. Đối với các kênh lót bê tông có độ cong lớn và vận tốc cao, nên sử dụng Phương trình 4.34 để tính toán.
Các vấn đề khác do đường cong của kênh trong dòng chảy dưới tới hạn bao gồm dòng chảy xoắn, thay đổi trong phân bố vận tốc, và gia tăng tổn thất ma sát trong kênh cong so với kênh thẳng.
Để biết thêm thông tin về dòng chảy quanh khúc cua, tham khảo các tài liệu sau:
- Rouse (1950)
- Chow (1959)
- Richardson et al. (2001)
4.6.6 Dòng chảy siêu tới hạn trong khúc cua
Việc thay đổi hướng của dòng chảy siêu tới hạn rất khó thực hiện. Nước di chuyển với vận tốc siêu tới hạn quanh các khúc cua sẽ tạo ra các sóng có thể “leo ra” khỏi kênh. Những sóng này có thể tiếp tục lan truyền xuống hạ lưu trong một khoảng cách dài.
Ngoài ra, những thay đổi đột ngột trong hướng dòng chảy có thể tạo ra nhảy thủy lực, làm nước tràn qua bờ kênh. Vì vậy, bất kỳ thay đổi hướng dòng chảy nào cũng nên được thực hiện ở phần đầu của đoạn kênh, trước khi vận tốc siêu tới hạn phát triển.
Nếu việc thay đổi hướng dòng chảy là bắt buộc trong một kênh có dòng chảy siêu tới hạn, thì kênh nên có mặt cắt hình chữ nhật và tốt nhất là được bao kín.
Trong các máng nhỏ (small chutes), các thí nghiệm đã chỉ ra rằng góc mở rộng (α) của biên kênh chữ nhật không nên vượt quá giá trị được xác định bởi phương trình:
$$\tan \alpha = \frac{1}{3 Fr} \tag{4.35}$$
Việc thay đổi hướng dòng chảy trong kênh hở có thể và nên được thiết kế để giảm tác động của sóng do sự thay đổi hướng dòng chảy gây ra (xem Richardson et al., 2001).
Trong nhiều trường hợp, các thiết kế liên quan đến dòng chảy siêu tới hạn nên được kiểm tra mô hình để phát triển thiết kế tối ưu hoặc thậm chí chỉ để đảm bảo thiết kế có thể hoạt động hiệu quả.
Ví dụ 4.7 – Kiểm tra tràn bờ tại khúc cua
Cho: Trong điều kiện dòng chảy lớn, một con suối trên núi sâu 2,0 m chảy gần đầy bờ với độ sâu normal là 1,8 m và vận tốc là 3,4 m/s.
Tại một khúc cua gấp:
- Bán kính cong phía ngoài: ro=12 m
- Bán kính cong đến tim kênh: rc = 10 m
- Bán kính cong phía trong: ri = 8 m
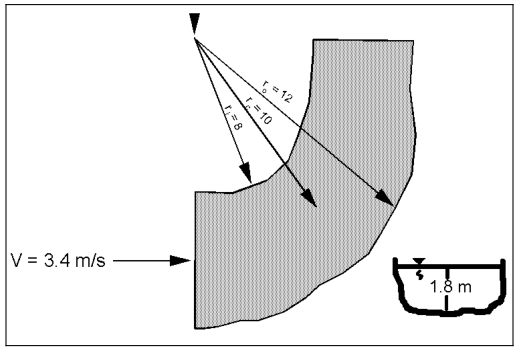
Hỏi: Dòng chảy có tràn qua bờ tại khúc cua không?
Giải: Sử dụng công thức nâng cao mặt nước (superelevation).
$$\Delta Z = \frac{V^2}{g r_c} (r_o – r_i) \qquad \Delta Z = \frac{3.4^2}{(9.81)(10)} (12 – 8) = 0.47\, \text{m}$$
Mặt nước dâng lên khoảng 0.47/2 m ở phía ngoài khúc cong và hạ thấp cùng một lượng ở phía trong khúc cong. Độ sâu dòng chảy lớn nhất trong khúc cong sẽ là:
$$y_{\text{outside}} = 1.8 + (0.47 / 2) = 2.04\, \text{m}$$
Mực nước tăng khoảng (0,47/2) m ở phía ngoài khúc cua và giảm cùng một lượng ở phía trong khúc cua.
điều này lớn hơn độ sâu của kênh (2,0 m), do đó dòng chảy sẽ tràn qua bờ.
4.7 Dòng chảy Thay Đổi Chậm (Garadually varied flow)
4.7.1 Giới thiệu
Trong phần này, một dạng thứ hai của dòng chảy ổn định được xem xét, đó là dòng chảy thay đổi chậm (gradually varied flow). Trong dòng chảy này, sự thay đổi độ sâu và vận tốc diễn ra từ từ trên một đoạn dài; lực cản dòng chảy đóng vai trò chính, còn các lực gia tốc được bỏ qua. Việc phân tích dòng chảy ổn định thay đổi chậm gồm hai nội dung chính:
(1) xác định các đặc điểm tổng quát của mặt nước; và
(2) xác định cao độ mặt nước hoặc độ sâu dòng chảy.
Trong dòng chảy thay đổi chậm, độ sâu dòng chảy thực tế y có thể lớn hơn hoặc nhỏ hơn normal depth (y0), và cũng có thể lớn hơn hoặc nhỏ hơn độ sâu tới hạn (yc). Các đường mặt nước – water surface profile thường được gọi là đường cong backwater – phụ thuộc vào độ sâu thực tế y so với normal depth (y0) và độ sâu tới hạn (yc).
Normal depth y0 là độ sâu dòng chảy tương ứng với điều kiện chảy đều ổn định, được xác định bằng phương trình Manning.
Độ sâu tới hạn yc là độ sâu tại đó số Froude bằng 1.0.
Nguyên nhân khiến độ sâu thực tế khác với normal depth bao gồm:
- thay đổi độ dốc đáy kênh,
- thay đổi tiết diện dòng chảy,
- vật cản trên dòng,
- sự mất cân bằng giữa lực trọng trường (làm tăng tốc dòng) và lực cản (làm giảm tốc dòng).
Khi làm việc với dòng chảy ổn định thay đổi chậm, bước đầu tiên là xác định loại đường mặt nước – water surface profile có thể xảy ra. Bước tiếp theo là thực hiện các tính toán số. Một tài liệu tham khảo kinh điển về dòng chảy này là Chow (1959).
4.7.2 Các loại đường mặt nước (water surface profiles)
Các loại đường mặt nước (water surface profiles) được xác định bằng cách phân tích sự thay đổi của các đại lượng trong phương trình dòng chảy thay đổi chậm:
$$\frac{dy}{dx} = S_o \left\{ \frac{1 – \left( \frac{n}{n_0} \right)^2 \left( \frac{y_0}{y} \right)^{10/3}}{1 – \left( \frac{y_c}{y} \right)^3} \right\} \tag{4.36}$$
(đây là phương trình vi phân biểu diễn sự thay đổi độ sâu dòng chảy y theo chiều dọc x trong dòng chảy thay đổi chậm – gradually varied flow),
trong đó:
- \(\frac{dy}{dx}\): độ dốc mặt nước (water surface slope)
- So: độ dốc đáy kênh
- n: hệ số nhám Manning tại vị trí đang xét
- n0: hệ số nhám Manning chuẩn
- y0: độ sâu normal (normal depth)
- yc: độ sâu tới hạn (critical depth)
- y: độ sâu thực tế tại vị trí đang xét
Phương trình này thường được giải bằng phương pháp số để xác định đường mặt nước trong các điều kiện dòng chảy thay đổi chậm.
Độ dốc của mặt nước \(\frac{dy}{dx}\) phụ thuộc vào độ dốc đáy kênh So, tỷ số giữa normal depth (yo) và độ sâu thực tế (y), cũng như tỷ số giữa critical depth (yc) và độ sâu thực tế (y).
Sự khác biệt giữa lực cản dòng chảy trong điều kiện đều – ổn định (no) và lực cản dòng chảy trong điều kiện không đều – ổn định (n) là nhỏ, nên tỷ số này được lấy bằng 1,0. Với n=no có 12 loại water surface profiles. 12 loại này được chia thành 5 nhóm dựa trên độ dốc đáy kênh. Các loại water surface profile này được minh họa trong Hình 4.15 và tóm tắt trong Bảng 4.1.
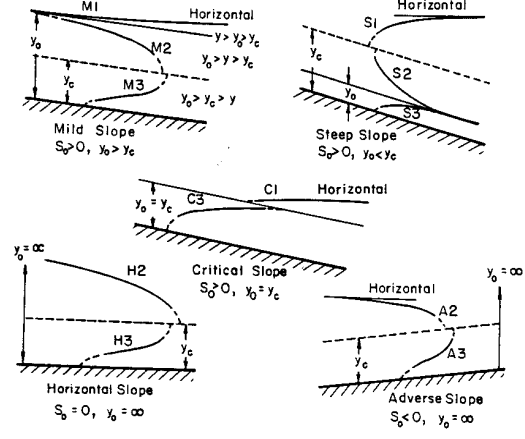
Khi y→yc, giả định lực gia tốc có thể được bỏ qua không còn đúng nữa. Phương trình 4.36 chỉ ra rằng dy/dx vuông góc với độ dốc đáy khi y→yc. Đối với các vị trí gần mặt cắt ngang nơi dòng chảy ở trạng thái tới hạn, trong khoảng cách từ 3 đến 20 m (10 đến 65 ft), phân tích dòng chảy cong và thí nghiệm phải được sử dụng để xác định giá trị thực tế của y. Khi phân tích ở khoảng cách dài, từ 30 đến 100 m hoặc hơn (100 đến 300 ft hoặc hơn), có thể giả định một cách định tính rằng y đạt đến yc.
Nói chung, khi dòng chảy nhanh (Fr>1), dòng chảy không thể trở nên êm dịu hoặc dưới tới hạn mà không xảy ra một cú nhảy thủy lực. Ngược lại, dòng chảy dưới tới hạn có thể trở nên nhanh hơn, hoặc siêu tới hạn (vượt qua đường mực nước tới hạn). Điều này được minh họa trong Hình 4.16
(nd: độ dốc thẳng đứng của đường mặt nước)
Phương trình 4.36 mô tả sự thay đổi của mực nước dòng chảy (\(\frac{dy}{dx}\)) theo độ dốc đáy So và các thông số thủy lực khác.
Xét mẫu số của phương trình: $$1-\left(\frac{y_c}y\right)^3$$
- Khi y→yc, biểu thức \(\left(\frac{y_c}y\right)^3\) →1, dẫn đến mẫu số tiến đến 0.
- Điều này làm cho dy/dx tiến đến vô cùng (±∞), tức là đường nước trở nên thẳng đứng.
Một độ dốc nước thẳng đứng có nghĩa là dòng chảy có sự gián đoạn mạnh, đây chính là biểu hiện của một cú nhảy thủy lực (hydraulic jump) hoặc điểm tới hạn của dòng chảy. Khi đó, dy/dx vuông góc với đáy.
Điều này phù hợp với thực tế thủy lực:
- Khi y→yc, dòng chảy không thể tiếp tục duy trì trạng thái ổn định mà không có sự chuyển đổi mạnh.
- Nếu dòng chảy là siêu tới hạn (Fr>1), nó cần một cú nhảy thủy lực để trở về dưới tới hạn.
- Nếu dòng chảy là dưới tới hạn (Fr<1), nó có thể tự nhiên chuyển thành siêu tới hạn khi điều kiện thuận lợi (ví dụ: khi dốc đáy tăng).
Vì vậy, phương trình 4.36 giải thích tại sao gần mực nước tới hạn yc, hệ số biến đổi mực nước dy/dx trở nên cực lớn, dẫn đến độ dốc nước vuông góc với đáy kênh.
Khi có sự thay đổi trong mặt cắt ngang, độ dốc hoặc có vật cản trong dòng chảy, phân tích định tính về profile mực nước phụ thuộc vào việc xác định các điểm khống chế, xác định loại profile mực nước ở thượng lưu và hạ lưu của các điểm khống chế, sau đó phác thảo các profile này.
Cần nhớ rằng khi dòng chảy ở trạng thái siêu tới hạn (Fr>1), độ sâu khống chế nằm ở thượng lưu và phân tích profile mực nước được thực hiện theo hướng dòng chảy. Ngược lại, khi dòng chảy ở trạng thái dưới tới hạn (Fr<1), độ sâu khống chế nằm ở hạ lưu và các phép tính phải được thực hiện theo hướng ngược dòng về thượng lưu.
Các profile mực nước hình thành do sự thay đổi độ dốc đáy kênh được minh họa trong Hình 4.16.

| Loại | Độ dốc đáy | Độ sâu | Loại | Phân loại |
|---|---|---|---|---|
| Nhẹ (Mild) | So > 0 | y > yo > yc | 1 | M1 |
| Nhẹ (Mild) | So > 0 | yo > y > yc | 2 | M2 |
| Nhẹ (Mild) | So > 0 | yo > yc > y | 3 | M3 |
| Tới hạn (Critical) | So > 0 | y > yo = yc | 1 | C1 |
| Tới hạn (Critical) | So > 0 | y < yo = yc | 3 | C3 |
| Dốc (Steep) | So > 0 | y > yc > yo | 1 | S1 |
| Dốc (Steep) | So > 0 | yc > y > yo | 2 | S2 |
| Dốc (Steep) | So > 0 | yc > yo > y | 3 | S3 |
| Nằm ngang (Horizontal) | So = 0 | y > yc | 2 | H2 |
| Nằm ngang (Horizontal) | So = 0 | yc > y | 3 | H3 |
| Ngược dốc (Adverse) | So < 0 | y > yc | 2 | A2 |
| Ngược dốc (Adverse) | So < 0 | yc > y | 3 | A3 |
Bảng 4.1. Đặc điểm của Water Surface Profiles
Lưu ý:
- Với đường cong loại 1 (M1, S1, C1), độ sâu thực tế của dòng chảy y lớn hơn cả độ sâu normal yo và độ sâu tới hạn yc. Vì dòng chảy êm dịu, nên điểm khống chế nằm ở hạ lưu.
- Với đường cong loại 2 (M2, S2, A2, H2), độ sâu thực tế y nằm giữa độ sâu normal yo và độ sâu tới hạn yc. Dòng chảy êm đối với M2, A2 và H2, do đó điểm khống chế nằm ở hạ lưu. Dòng chảy nhanh đối với S2, nên điểm khống chế nằm ở thượng lưu.
- Với đường cong loại 3 (M3, S3, C3, A3, H3), độ sâu thực tế y nhỏ hơn cả độ sâu normal yo và độ sâu tới hạn yc. Vì dòng chảy nhanh, nên điểm khống chế nằm ở thượng lưu.
- Đối với độ dốc nhẹ (mild slope), So nhỏ hơn Sc và yo>yc.
- Đối với độ dốc lớn (steep slope), So lớn hơn Sc và yo<yc.
- Đối với độ dốc tới hạn (critical slope), So bằng Sc và yo=yc.
- Đối với độ dốc ngược (adverse slope), So có giá trị âm.
- Đối với độ dốc nằm ngang (horizontal slope), So bằng không.
- Trường hợp y→yc là một điểm đặc biệt quan trọng vì khi đó, mẫu số trong Phương trình 4.36 tiến dần về 0.
Để xác định xem cú nhảy thủy lực xảy ra trên dốc lớn (steep slope) hay dốc nhẹ (mild slope), tính toán độ sâu sequent y2 cho độ sâu y1 bằng phương trình nhảy thủy lực.
- Nếu y2 từ phương trình nhảy thủy lực lớn hơn độ sâu normal yo tính theo phương trình Manning trên dốc nhẹ, thì sẽ xuất hiện đường cong M3 trên dốc nhẹ cho đến khi y2 đạt đến độ sâu tương ứng với độ sâu ban đầu cần thiết để cú nhảy xảy ra.
- Nếu y2 nhỏ hơn độ sâu cần thiết để cân bằng với độ sâu hạ lưu, cú nhảy thủy lực sẽ xảy ra trên dốc lớn và đường cong S1 sẽ xuất hiện để kết nối với độ sâu normal tại mặt cắt khống chế.
(nd: độ sâu normal và độ sâu tới hạn)
Trong thủy lực kênh hở, hai khái niệm quan trọng giúp xác định đặc điểm dòng chảy là độ sâu normal (yo) và độ sâu tới hạn (yc). Chúng có vai trò quan trọng trong việc phân loại các water surface profiles và xác định vị trí xảy ra cú nhảy thủy lực.
1. Độ sâu Normal (yo)
- Độ sâu normal là độ sâu của dòng chảy khi dòng chảy đạt trạng thái ổn định trên một đoạn kênh có độ dốc, mặt cắt ngang, và độ nhám không đổi.
- Nó được tính dựa vào phương trình Manning hoặc phương trình Chézy, tùy thuộc vào bài toán.
- Khi dòng chảy ở độ sâu normal, lực trọng trường cân bằng với lực ma sát đáy kênh, tức là năng lượng của dòng chảy không thay đổi theo thời gian.
- Độ sâu normal phụ thuộc vào:
- Lưu lượng dòng chảy (Q)
- Độ dốc đáy kênh (So)
- Hệ số nhám Manning (n)
- Hình dạng mặt cắt ngang của kênh.
🡺 Ý nghĩa: Nếu một kênh có dòng chảy duy trì ở độ sâu normal, dòng chảy không bị ảnh hưởng bởi các chướng ngại vật hoặc sự thay đổi đột ngột về hình dạng kênh.
2. Độ sâu Tới Hạn (yc) [độ sâu phân giới]
- Độ sâu tới hạn là độ sâu mà tại đó số Froude (Fr) bằng 1, tức là năng lượng riêng của dòng chảy đạt giá trị tối thiểu.
- Nó được xác định bởi phương trình tới hạn: $$y_c=(\frac{Q^2}{g\;B^2})^\frac13$$
- Trong đó:
- Q là lưu lượng dòng chảy,
- g là gia tốc trọng trường,
- B là chiều rộng mặt kênh tại mặt nước.
- Khi y=yc, vận tốc dòng chảy đúng bằng vận tốc sóng trọng lực, tức là không có sóng nào có thể truyền ngược lại dòng chảy.
- Độ sâu tới hạn xác định xem dòng chảy là siêu tới hạn (Fr > 1) hay dưới tới hạn (Fr < 1):
- Siêu tới hạn (y<yc): Dòng chảy nhanh, vận tốc cao, năng lượng chủ yếu ở dạng động năng.
- Dưới tới hạn (y>yc): Dòng chảy chậm, vận tốc thấp, năng lượng chủ yếu ở dạng thế năng.
🡺 Ý nghĩa: Độ sâu tới hạn là một điểm quan trọng để xác định điều kiện dòng chảy và vị trí kiểm soát thủy lực. Khi một kênh có độ sâu gần bằng độ sâu tới hạn, bất kỳ thay đổi nhỏ nào cũng có thể làm thay đổi đáng kể đặc điểm dòng chảy.
3. So sánh độ sâu Normal và độ sâu Tới Hạn
| Tiêu chí | Độ sâu Normal (yo) | Độ sâu Tới Hạn (yc) |
|---|---|---|
| Định nghĩa | Độ sâu tại đó dòng chảy đạt trạng thái ổn định theo Manning. | Độ sâu tại đó năng lượng riêng đạt tối thiểu, Fr = 1. |
| Phụ thuộc vào | Độ dốc đáy, lưu lượng, độ nhám, hình dạng kênh. | Lưu lượng và mặt cắt ngang. |
| Tác động lên dòng chảy | Xác định trạng thái ổn định của dòng chảy. | Xác định sự chuyển đổi giữa dòng chảy dưới tới hạn và siêu tới hạn. |
| Liên quan đến cú nhảy thủy lực | Dòng chảy có thể thay đổi để đạt đến độ sâu normal sau cú nhảy thủy lực. | Độ sâu tới hạn là điểm mà cú nhảy thủy lực có thể bắt đầu. |
4. Ứng dụng của yo và yc trong phân tích thủy lực
- Khi dốc kênh nhẹ (So<Sc), ta có yo>yc, tức là dòng chảy có xu hướng ổn định ở trạng thái dưới tới hạn.
- Khi dốc kênh lớn (So>Sc), ta có yo<yc, tức là dòng chảy có xu hướng siêu tới hạn.
- Khi có vật cản hoặc thay đổi hình dạng kênh, dòng chảy có thể thay đổi giữa các trạng thái và tạo ra cú nhảy thủy lực.
- Khi dòng chảy chuyển từ siêu tới hạn (Fr>1) sang dưới tới hạn (Fr<1), cú nhảy thủy lực sẽ xảy ra, và việc tính toán yo và yc giúp xác định vị trí xảy ra cú nhảy.
5. Tóm lại
- Độ sâu normal dùng để xác định trạng thái ổn định của dòng chảy theo Manning.
- Độ sâu tới hạn dùng để xác định ngưỡng chuyển đổi giữa dòng chảy dưới tới hạn và siêu tới hạn.
- Trong thực tế, việc tính toán và so sánh yo và yc giúp kỹ sư thủy lực hiểu rõ hơn về đặc điểm dòng chảy và dự đoán vị trí xảy ra các hiện tượng quan trọng như cú nhảy thủy lực hoặc sự thay đổi trong water surface profiles.
Ví dụ 4.8 – Xác định loại và cú nhảy thủy lực
Cho: Một kênh hình chữ nhật rộng 5 m chuyển từ một độ dốc rất lớn sang một dốc nhẹ.
- Lưu lượng thiết kế: 24,8 m³/s.
- Trên dốc lớn, độ sâu normal và vận tốc lần lượt là 0,33 m và 15 m/s.
- Trên dốc nhẹ, độ sâu normal và vận tốc lần lượt là 2,96 m và 1,68 m/s.
Hỏi:
- Xác định loại dòng chảy xảy ra trong cả hai kênh.
- Nếu có cú nhảy thủy lực, xác định:
- Độ sâu hạ lưu sau cú nhảy.
- Vị trí xảy ra cú nhảy.
- Phân loại water surface profile.
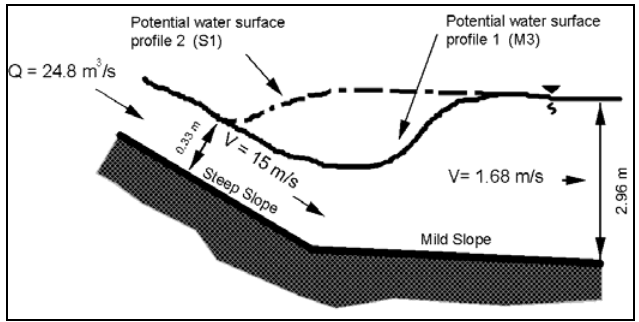
Giải:
1. Tìm độ sâu tới hạn (yc) trên dốc lớn, ta sử dụng phương trình độ sâu tới hạn cho kênh chữ nhật:
Công thức tính độ sâu tới hạn trong kênh chữ nhật:
$$y_c = \left( \frac{q^2}{g} \right)^{1/3} \quad \text{với} \quad q = \frac{Q}{B} \text{ (B là chiều rộng kênh)}$$
Thay vào:
$$y_c = \left( \frac{(Q/B)^2}{g} \right)^{1/3} \quad \Rightarrow \quad y_c = \left( \frac{(24.8 / 5)^2}{9.81} \right)^{1/3} = 1.36 \, \text{m}$$
Vậy độ sâu tới hạn ycy_c của dòng chảy là 1.36 mét.
Trên dốc lớn, độ sâu normal là 0,33 m. Vì y<yc, dòng chảy siêu tới hạn xảy ra trên dốc lớn. Lưu ý rằng lưu lượng đơn vị (q) là như nhau cho cả dốc nhẹ, do đó, yc là giống nhau cho cả đoạn dốc lớn và dốc nhẹ. Trên dốc nhẹ, độ sâu normal là 2,96 m. Vì y>yc, dòng chảy dưới tới hạn xảy ra trên dốc nhẹ. Do đó, cú nhảy thủy lực sẽ xảy ra.
2. Tiếp theo, xác định xem cú nhảy thủy lực sẽ xẩy ra trên dốc lớn hay dốc nhẹ
Để xác định cú nhảy thủy lực xảy ra trên dốc lớn hay dốc nhẹ, ta cần tính độ sâu kế tiếp (y2) cho độ sâu y1 trên dốc lớn, sử dụng phương trình cú nhảy thủy lực.
- Nếu y2 từ phương trình cú nhảy thủy lực lớn hơn độ sâu normal yo tính theo phương trình Manning trên dốc nhẹ, thì sẽ xuất hiện một đường cong M3 trên dốc nhẹ cho đến khi y2 đạt đến độ sâu tới hạn.
- Nếu y2 nhỏ hơn yo trên dốc nhẹ, cú nhảy có thể xảy ra trên dốc lớn và một đường cong S1 sẽ xuất hiện để kết nối với độ sâu normal tại mặt cắt khống chế.
Công thức tính độ sâu sau nhảy thủy lực
$$y_2 = \frac{y_1}{2} \left( \sqrt{1 + 8 Fr_1^2} – 1 \right)$$
Tính số Froude:
$$Fr = \frac{V}{\sqrt{g y}} = \frac{15}{\sqrt{9.81 \cdot 0.33}} = 8.34$$
Thay vào công thức:
$$y_2 = \frac{0.33}{2} \left( \sqrt{1 + 8 (8.34)^2} – 1 \right) = 3.73\, \text{m}$$
Vậy độ sâu dòng chảy sau nhảy thủy lực là 3.73 mét.
So sánh các tham số và xác định loại water surface profile: Vì độ sâu kế tiếp (y2) lớn hơn độ sâu normal trên dốc nhẹ (tức là 3.73 > 2.96), kênh trên dốc nhẹ sẽ có đường cong M3 cho đến khi cú nhảy thủy lực xảy ra.
4.7.3 Phương pháp Bước Chuẩn (Standard Step Procedure)
Phương pháp bước chuẩn là một quy trình tính toán đơn giản để xác định water surface profile trong dòng chảy thay đổi dần. Việc xác định trước loại water surface profile, như đã phân tích trong phần trước, sẽ giúp xác định hướng tính toán nên tiến hành theo thượng lưu hay hạ lưu. Phương pháp bước chuẩn được suy ra từ phương trình năng lượng. Phương trình đó là:
$$\Delta L = \frac{H_1 – H_2}{S_o – S_f}$$
Trong đó:
- ΔL = Khoảng cách giữa Mặt cắt 1 và Mặt cắt 2, m (ft)
- H = Năng lượng riêng tại Mặt cắt 1 và 2, m (ft)
- So = Độ dốc đáy kênh
- Sf = Độ dốc ma sát
Phương trình trên được sử dụng trong phương pháp bước chuẩn. Một ví dụ về ứng dụng của phương pháp bước chuẩn có thể được tìm thấy trong Chow (1959) và Richardson et al. (2001).
Mặc dù các chương trình máy tính (chẳng hạn như HEC-RAS) thường được sử dụng để tính toán water surface profiles, nhưng nên thực hiện một bản phác thảo định tính về water surface profiles dựa trên thông tin đã trình bày trong phần trước.
Điều này đặc biệt hữu ích trong các trường hợp profile phức tạp, khi độ dốc kênh thay đổi từ dốc lớn sang dốc nhẹ hoặc dốc nhẹ sang dốc lớn.
Hỗ trợ duy trì trang:
Tôi xây dựng trang này để chia sẻ các tài liệu kỹ thuật cốt lõi trong thiết kế hạ tầng giao thông.
Nếu bạn thấy nội dung hữu ích và muốn góp phần duy trì trang hoạt động bền vững, tôi rất trân trọng mọi sự ủng hộ.