7 Dòng chảy trong ống kín

7.1 Các loại dòng chảy trong ống kín

Trong ống kín, dòng chảy có thể xảy ra dưới ba dạng: dòng chảy kênh hở, dòng chảy đầy do trọng lực và dòng chảy áp lực.

• Dòng chảy kênh hở xảy ra khi mặt nước tiếp xúc với khí quyển, có thể xuất hiện trong kênh hở hoặc trong ống kín nhưng chưa đầy nước. Phân tích dòng chảy kênh hở trong ống kín tương tự như bất kỳ loại dòng chảy kênh hở nào khác, và tất cả các khái niệm, nguyên tắc đã thảo luận trong Chương 4 đều được áp dụng.
• Dòng chảy đầy do trọng lực (Gravity Full Flow) xảy ra khi ống chảy đầy nước nhưng chưa có áp suất.
• Dòng chảy áp lực (Pressure Flow) xảy ra khi ống chảy đầy nước và chịu áp suất.

Do diện tích ướt (wetted perimeter) lớn hơn và ma sát tăng trong ống đầy nước, một ống chảy một phần thường có thể vận chuyển lưu lượng lớn hơn. Đối với ống tròn, lưu lượng đỉnh xảy ra khi mức nước đạt 93% chiều cao ống, và vận tốc trung bình khi ống đầy một nửa tương đương với vận tốc của dòng chảy đầy do trọng lực (Hình 7.1).

(nd)

V/V_full (Tốc độ dòng chảy so với khi ống đầy)

Q/Q_full (Lưu lượng so với khi ống đầy)

A/A_full (Diện tích mặt cắt dòng chảy so với khi ống đầy)

R/R_full (Bán kính thủy lực so với khi ống đầy)

Các đường cong trên biểu đồ thể hiện sự thay đổi của:

• Lưu lượng (Discharge)
• Diện tích mặt cắt dòng chảy (Area)
• Bán kính thủy lực (Hydraulic Radius)
• Tốc độ dòng chảy (Velocity)

Biểu đồ này cho thấy rằng lưu lượng cực đại xảy ra khi mực nước đạt khoảng 93% đường kính ống, và tốc độ trung bình khi ống đầy một nửa tương đương với tốc độ của dòng chảy đầy do trọng lực.

Điều kiện dòng chảy đầy do trọng lực thường được giả định trong thiết kế hệ thống thoát nước mưa. Phương trình Manning (Phương trình 4.5) cho mặt cắt tròn chảy đầy có thể được viết lại như sau:

$$Q = \left( \frac{K_u}{n} \right) D^{8/3} S^{1/2} \tag{7.1}$$

trong đó:

• Q = Lưu lượng, m³/s (ft³/s)
• n = Hệ số nhám Manning
• D = Đường kính ống, m (ft)
• S = Độ dốc, m/m (ft/ft)
• K_u = Hệ số chuyển đổi đơn vị, bằng 0.312 (0.46 trong hệ đơn vị Anh)

Phương trình này cho phép tính trực tiếp đường kính ống cần thiết. Lưu ý rằng đường kính tính toán phải được tăng lên một kích thước danh nghĩa lớn hơn để có thể vận chuyển lưu lượng thiết kế mà không tạo ra dòng chảy áp lực.

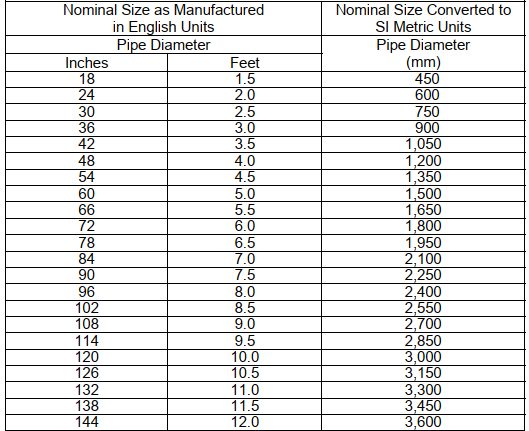
Các kích thước danh nghĩa tiêu chuẩn theo hệ SI, dựa trên các kích thước danh nghĩa hiện tại của hệ đơn vị Anh, được trình bày trong Bảng 7.1.

Ví dụ 7.1

Cho:
Nước mưa trên mặt đường được thu gom bằng một loạt cửa thu nước kết hợp. Trong điều kiện thiết kế, tổng lưu lượng thu gom từ tất cả các cửa thu là 0.4 m³/s.

Một ống thoát nước mưa bằng bê tông (n = 0.013) sẽ được lắp đặt với độ dốc song song với độ dốc mặt đường, có giá trị 0.005 m/m.

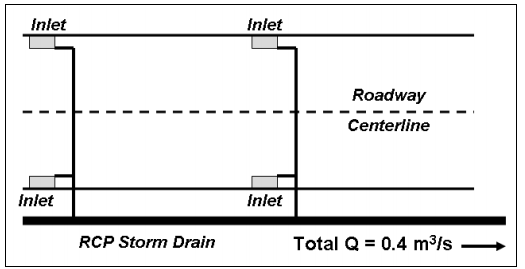
Tìm:

1. Đường kính ống thoát nước mưa cần thiết để vận chuyển lưu lượng thiết kế 0.4 m³/s mà không tạo ra dòng chảy áp lực.
2. Vận tốc dòng chảy khi ống đầy nước.

Giải:

1. Sử dụng phương trình dòng chảy đầy (cho đường kính ống tính bằng mét):

$$Q = \left( \frac{K_u}{n} \right) D^{8/3} S^{1/2} \quad \text{với } K_u = 0.312 \text{ (đơn vị SI)}$$

$$0.4 = \left( \frac{0.312}{0.013} \right) D^{8/3} (0.005)^{1/2}$$

$$D^{8/3} = 0.236$$

$$D = 0.58 \, \text{m hoặc } 580 \, \text{mm}$$

2. Dựa trên Bảng 7.1, cỡ ống danh định lớn hơn tiếp theo là 600 mm.
3. Theo điều kiện thiết kế, ống 600 mm sẽ chảy hơi ít hơn mức đầy. Dựa vào mối quan hệ dòng chảy không đầy (Hình 7.1), vận tốc không thay đổi đáng kể giữa nửa đầy và đầy. Tuy nhiên, để tính thời gian tập trung (tc), cần dùng vận tốc dòng chảy không đầy.

Để tính vận tốc dòng chảy không đầy, có thể sử dụng biểu đồ nomograph hoặc phương pháp thử-sai. Ngoài ra, cũng có thể dùng các mối quan hệ dòng chảy không đầy. Lưu lượng và vận tốc dòng chảy đầy cho ống bê tông đường kính 600 mm như sau:

$$Q = \left( \frac{0.312}{0.013} \right) (0.60)^{8/3} (0.005)^{1/2} = 0.43 \, \text{m}^3/\text{s}$$

$$V = \frac{Q}{A} = \frac{0.43}{\left[ \frac{\pi (0.6)^2}{4} \right]} = 1.52 \, \text{m/s}$$

Tỉ số lưu lượng giữa dòng không đầy và dòng đầy là:

$$\frac{Q}{Q_f} = \frac{0.40}{0.43} = 0.93$$

Tỉ số vận tốc tương ứng là 1.13 (theo Hình 7.1).

Vậy nên:

$$V / V_f = 1.13 \quad \text{và} \quad V = 1.13 (1.52) = 1.72 \, \text{m/s}$$

7.2 Phương trình năng lượng

Phương trình năng lượng đã được xem xét trong Chương 3 (Phương trình 3.2). Về mặt đơn giản, phương trình này phát biểu rằng tổng năng lượng tại bất kỳ mặt cắt nào phải bằng tổng năng lượng tại một mặt cắt hạ lưu cộng với tổn thất năng lượng trên đoạn trung gian.

Năng lượng tổng thể được chia thành ba thành phần:

1. Năng lượng do vận tốc (velocity head)
2. Năng lượng do áp suất (pressure head)
3. Năng lượng do cao độ (elevation head)

Đường năng lượng (Energy Grade Line – EGL) biểu diễn tổng năng lượng tại bất kỳ mặt cắt nào. Tổn thất năng lượng được phân loại thành tổn thất do ma sát và tổn thất do hình dạng (form losses) (xem Mục 7.3).

Đường thủy lực (Hydraulic Grade Line – HGL) nằm thấp hơn EGL một khoảng bằng năng lượng do vận tốc.

• Trong dòng chảy kênh hở, HGL chính là mực nước trong kênh.
• Trong dòng chảy áp lực, HGL là mực nước dâng lên trong ống đứng được kết nối với ống chính.

Ví dụ, trong một hệ thống thoát nước mưa được thiết kế theo điều kiện dòng chảy áp lực, HGL phải thấp hơn cao độ mặt đường. Nếu không, nước trong cống có thể dâng lên qua các cửa thu nước và nắp hố ga, gây ngập mặt đường.

Tương tự, nếu hệ thống thoát nước mưa hoạt động trong điều kiện dòng chảy siêu tới hạn (supercritical flow), cần đảm bảo rằng không xảy ra cú nhảy thủy lực (hydraulic jump), vì nó có thể tạo ra dòng chảy áp lực và làm cho HGL cao hơn cao độ mặt đường, gây ra ngập lụt.

7.3 Tổn thất năng lượng

Khi sử dụng phương trình năng lượng, cần tính toán đầy đủ tất cả các tổn thất năng lượng. Tổn thất năng lượng có thể được phân thành hai loại:

1. Tổn thất do ma sát (friction losses): Gây ra bởi lực ma sát giữa dòng chảy và vật liệu thành ống.
2. Tổn thất do hình dạng (form losses): Phát sinh do các cấu trúc thủy lực khác nhau dọc theo tuyến ống kín.

Các cấu trúc này bao gồm:

• Hố ga (access holes)
• Đoạn uốn cong (bends)
• Đoạn thu hẹp (contractions)
• Đoạn mở rộng (enlargements)
• Đoạn chuyển tiếp (transitions)

Mỗi cấu trúc trên đều gây ra tổn thất do vận tốc (velocity headlosses) và có thể làm thay đổi đáng kể đường năng lượng (EGL) cũng như đường thủy lực (HGL) tại vị trí đó.

Tổn thất do hình dạng thường được gọi là “tổn thất nhỏ” (minor losses) vì chúng thường nhỏ hơn đáng kể so với tổn thất do ma sát.

7.3.1 Tính toán tổn thất do ma sát

Tổn thất do ma sát được tính như sau:

$$h_f = L \cdot S_f \tag{7.2}$$

trong đó:

L = Chiều dài của ống dẫn

S_f = Độ dốc ma sát (độ dốc của đường năng lượng
Dòng chảy đều thường được giả định để có thể tính độ dốc ma sát bằng phương trình Manning hoặc phương trình Darcy–Weisbach. Viết lại phương trình Manning cho S_f:

$$S_f = \left( \frac{Qn}{K_u A R^{2/3}} \right)^2 \tag{7.3}$$

Phương trình Darcy–Weisbach cho dòng chảy kênh hở:

$$S_f = \frac{f}{4R} \cdot \frac{V^2}{2g} \tag{7.4}$$

và cho dòng áp lực trong ống tròn:

$$h_f = \frac{fL}{D} \cdot \frac{V^2}{2g} \tag{7.5}$$

Phương trình Manning thường được sử dụng nhiều hơn bởi các kỹ sư thực hành, mặc dù phương trình Darcy–Weisbach là phương trình tốt hơn về mặt lý thuyết vì nó đúng về mặt đơn vị và áp dụng cho bất kỳ loại chất lỏng nào trong nhiều điều kiện khác nhau. Tuy nhiên, khả năng đạt độ chính xác cao hơn với phương trình Darcy–Weisbach bị giới hạn bởi việc phải xác định hệ số Darcy f, và thường yêu cầu quy trình phức tạp hơn so với phương trình Manning. Các giá trị hệ số Manning n điển hình cho dòng chảy trong ống kín được trình bày trong Phụ lục B, Bảng B.3.

Dù sử dụng công thức nào, việc đánh giá là cần thiết khi chọn hệ số nhám. Hệ số nhám chủ yếu được xác định theo loại vật liệu ống, tuy nhiên, nhiều yếu tố khác có thể làm thay đổi giá trị này. Các yếu tố quan trọng khác bao gồm loại mối nối, độ thẳng hàng và độ dốc do lún hoặc chuyển vị đất bên, lớp bồi lắng trầm tích và dòng chảy từ các nhánh bên vào dòng chính.

7.3.2 Tính toán tổn thất do hình dạng

Tổn thất cục bộ (form losses) xảy ra khi dòng chảy đi qua các công trình như: miệng hố ga, mối nối, đoạn cong, thu hẹp, mở rộng và các đoạn chuyển tiếp. Những cấu trúc này có thể gây ra tổn thất lớn cả trong đường năng lượng (energy grade line) và đường thủy lực (hydraulic grade line) khi đi qua công trình, và nếu không được tính đến trong thiết kế, khả năng thoát nước của ống dẫn có thể bị hạn chế.

Tổn thất cục bộ có thể được đánh giá theo nhiều phương pháp. Phương pháp đơn giản nhất dựa trên hệ số nhân với cột nước vận tốc, với các hệ số khác nhau được tra bảng cho các trường hợp như: tổn thất vào/ra, đoạn cong, đoạn mở rộng, thu hẹp, v.v. Dạng tổng quát của phương trình là:

$$h_L = K \cdot \frac{V^2}{2g} \tag{7.6}$$

Tài liệu HEC-22 (Brown và các cộng sự, 2008) cung cấp các giá trị hệ số K cho các tình huống trên.

7.3.3 Tổn thất tại giao nối ống(Junction Losses)

Một mối nối ống (pipe junction) là chỗ nối của một ống nhánh vào một ống chính lớn hơn mà không sử dụng hố ga. Tổn thất cột nước tại mối nối có thể được tính bằng Phương trình 7.6 với một giá trị hệ số K thích hợp. Một phương pháp tinh vi hơn, được khuyến nghị bởi FHWA, dựa trên các nguyên lý về áp suất và động lượng, cụ thể là: tổng các lực tác động tại mối nối phải bằng tổng các động lượng, được biểu diễn như sau:

$$H_j = \frac{(Q_o V_o) – (Q_i V_i) – (Q_1 V_1 \cos \theta)}{0.5\, g\, (A_o + A_i)} + h_i – h_o \tag{7.7}$$

trong đó:

• Hj = Tổn thất cột áp tại nút giao, m (ft)
• Qo, Qi, Q1 = Lưu lượng tại ống đầu ra, đầu vào và ống nhánh, lần lượt, m³/s (ft³/s)
• Vo, Vi, V1 = Vận tốc tại ống đầu ra, đầu vào và ống nhánh, lần lượt, m/s (ft/s)
• ho, hi = Cột áp vận tốc tại đầu ra và đầu vào, m (ft)
• Ao, Ai = Diện tích mặt cắt ngang của ống đầu ra và đầu vào, m² (ft²)
• θ = Góc giữa ống nhánh và trục của ống đầu ra, độ
• g = Gia tốc trọng trường, 9.81 m/s² (32.2 ft/s²)

7.3.4 Tính toán tổn thất tại hố ga

Một tình huống phức tạp hơn xảy ra khi có một hố ga hoặc miệng vào tại điểm nối giữa ống vào và ống ra. Phương pháp đơn giản nhất dựa trên Phương trình 7.6 với một giá trị K tương ứng cho hố ga. Ví dụ, một giá trị K điển hình cho một hố ga thẳng không thay đổi đường kính ống là 0.15. FHWA gọi đây là phương pháp xấp xỉ và xem nó chỉ phù hợp cho ước lượng thiết kế sơ bộ, không nên sử dụng khi thực hiện các tính toán đường năng lượng (EGL).

Trong nhiều năm, FHWA đã phát triển và cải tiến các phương pháp phức tạp hơn để ước tính tổn thất tại hố ga và miệng vào. Phương pháp được khuyến nghị bởi FHWA để tính toán chính xác tổn thất cột nước tại hố ga phân loại hố ga và điều kiện thủy lực của chúng theo cách tương tự như kiểm soát tại miệng vào và dòng đầy trong cống, như được trình bày chi tiết trong HEC-22 (Brown và cộng sự, 2008). Ba bước cơ bản trong phương pháp của FHWA là:

BƯỚC 1: Xác định mực năng lượng ban đầu tại hố ga (Eₐᵢ) dựa trên kiểm soát tại cửa ra (dòng đầy hoặc không đầy) hoặc kiểm soát tại cửa vào (công thức đập tràn hoặc lỗ) đối với ống ra.

BƯỚC 2: Điều chỉnh mực năng lượng ban đầu tại hố ga dựa trên hình dạng hố, góc dòng vào, và điều kiện dòng đổ trực tiếp để tính mực năng lượng cuối cùng (Eₐ).

BƯỚC 3: Tính toán tổn thất đầu tại đầu vào từ mỗi ống vào và ước lượng đường thế năng (EGLₒ), sau đó sử dụng để tiếp tục tính toán ngược dòng.

Hình 7.2 tóm tắt các biến số chính được sử dụng trong quy trình này, quy trình sẽ được mô tả từng bước trong phần tiếp theo.

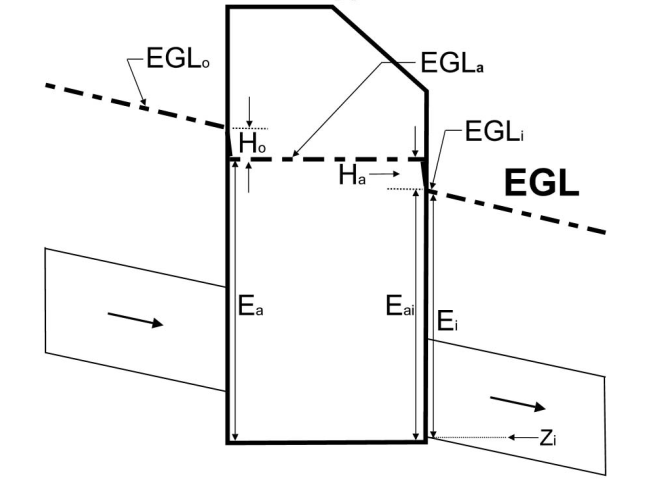
BƯỚC 1: Xác định mức năng lượng ban đầu tại hố ga

1. Điều kiện kiểm soát ở cửa ra (Outlet Control Condition)

• Điều kiện dòng chảy đầy dưới sự kiểm soát ở cửa ra: Đây là trường hợp phổ biến khi hệ thống thoát nước mưa bị dâng nước do mực nước hạ lưu cao (high tailwater) hoặc khi lưu lượng trong ống bị giới hạn bởi khả năng vận chuyển của ống.
• Điều kiện dòng chảy không đầy dưới sự kiểm soát ở cửa ra: Xảy ra khi ống thoát ra chảy không đầy và dòng chảy ở trạng thái dưới tới hạn (subcritical flow).

2. Điều kiện kiểm soát cửa vào (ngập nước): Xảy ra khi kích thước lỗ mở từ hố ga đến ống thoát ra bị hạn chế, dẫn đến mực nước trong hố ga đủ cao để dòng chảy qua lỗ mở được xem như dòng chảy qua lỗ (orifice flow).

3. Điều kiện kiểm soát cửa vào (không ngập nước): Xảy ra khi kích thước lỗ mở từ hố ga đến ống thoát ra cũng bị hạn chế, nhưng mực nước trong hố ga thấp hơn, khiến dòng chảy qua lỗ mở được xem như dòng chảy kiểu đập tràn (weir flow).

Về mặt đại số, mực năng lượng ban đầu có thể được biểu diễn như sau:

$$E_{ai} = \max(E_{aio}, E_{ais}, E_{aiu}) \tag{7.8}$$

trong đó:
    E_aio = Mực năng lượng tại hố ga ước tính theo kiểm soát tại cửa ra (dòng đầy và không đầy)
    E_ais = Mực năng lượng tại hố ga ước tính theo kiểm soát tại cửa vào (bị ngập)
    E_aiu = Mực năng lượng tại hố ga ước tính theo kiểm soát tại cửa vào (không bị ngập)

Ước lượng mực năng lượng cho kiểm soát tại cửa ra: dòng chảy không đầy và dòng đầy

Trong điều kiện kiểm soát tại cửa ra, lưu lượng ra khỏi hố ga bị giới hạn bởi hệ thống thoát nước phía hạ lưu sao cho ống thoát đang chảy đầy hoặc gần đầy ở trạng thái dòng dưới tới hạn. Mực năng lượng tại công trình (ước tính E_aio) được tính như sau:

$$E_{aio} = E_i + H_i \tag{7.9}$$

trong đó:
    E_i = Cột năng lượng riêng của ống thoát (tính theo Phương trình 7.10)
    H_i = Tổn thất tại lối vào, giả định kiểm soát tại cửa ra (tính theo Phương trình 7.11)

$$E_i = EGL_i – Z_i \tag{7.10}$$

$$H_i = K_i \cdot \left( \frac{V^2}{2g} \right) \tag{7.11}$$

trong đó:
    K_i = Hệ số tổn thất tại cửa vào = 0.2, không thứ nguyên

Ước tính mức năng lượng cho trường hợp kiểm soát tại cửa vào: Ngập nước

Tính toán kiểm soát tại cửa vào sử dụng một tỷ số không thứ nguyên được điều chỉnh từ phân tích cống, gọi là cường độ lưu lượng (discharge intensity). Cường độ lưu lượng được biểu diễn bởi tham số Discharge Intensity (DI), là tỷ số giữa lưu lượng và kích thước ống:

$$DI = \frac{Q}{A \cdot (g D_o)^{1/2}} \tag{7.12}$$

trong đó:
    A = Diện tích ống thoát, m² (ft²)
    D_o = Đường kính ống thoát, m (ft)

Điều kiện kiểm soát tại cửa vào khi bị ngập sử dụng mô hình tương tự lỗ thoát (orifice analogy) để ước lượng mức năng lượng

$$E_{ais} = D_o \cdot (DI)^2 \tag{7.13}$$

Phương trình 7.13 được xây dựng dựa trên dữ liệu có giá trị DI nhỏ hơn hoặc bằng 1.6.

Ước lượng mức năng lượng cho kiểm soát tại cửa vào: Không bị ngập

Các phân tích trong phòng thí nghiệm cho thấy điều kiện kiểm soát tại cửa vào không bị ngập có liên quan đến giá trị DI trong khoảng 0.0 đến 0.5 (mặc dù không có nghĩa là phương trình bị giới hạn trong khoảng này). Trong trường hợp này, mô hình tương tự đập tràn (weir analogy) được sử dụng để ước tính mức năng lượng

$$E_{aiu} = 1.6 \cdot D_o \cdot (DI)^{2/3} \tag{7.14}$$

BƯỚC 2: Điều chỉnh mức năng lượng do ảnh hưởng của sàn hố ga, góc nhập lưu và dòng chảy rơi

Mực năng lượng tại công trình được tính trong BƯỚC 1 được sử dụng làm cơ sở để ước lượng các tổn thất bổ sung do:
(1) dòng chảy vào công trình với góc khác 180 độ;
(2) cấu hình sàn (benching) – benching giúp hướng dòng chảy theo lòng hố ga và giảm tổn thất năng lượng;
(3) dòng chảy đổ xuống từ cao vào công trình (plunging flows) – các dòng này có cao độ lớn hơn mặt nước trong hố ga (dòng chảy từ cửa vào cũng có thể xem là plunging flows).

Ảnh hưởng của các điều kiện này có thể được ước lượng và áp dụng vào mực năng lượng ban đầu tại hố ga bằng nguyên lý chồng chất (superposition). Cách tiếp cận cộng dồn này giúp tránh hiện tượng sai số lớn trong các phương pháp khác, khi mà một hệ số nhân duy nhất dẫn đến giá trị tổn thất cực đoan. Phương trình được sử dụng là:

$$E_a = E_{ai} + H_B + H_\theta + H_P \tag{7.15}$$

trong đó:
    H_B = tổn thất năng lượng bổ sung do cấu hình sàn (benching)
    H_θ = tổn thất năng lượng bổ sung do dòng vào với góc khác 180 độ
    H_P = tổn thất năng lượng bổ sung do dòng đổ xuống từ cao

HEC-22 trình bày chi tiết các phương trình cần thiết để tính đến những yếu tố bổ sung này trong cấu hình hố ga. Lưu ý rằng E_a biểu diễn mức năng lượng tại hố ga (energy grade line – EGL). Nếu E_a nhỏ hơn cột năng lượng tại ống thoát E_i, thì E_a sẽ được đặt bằng E_i. Độ sâu mực nước trong hố ga y_a xấp xỉ bằng E_a.

Khi đã biết mức năng lượng tại hố ga E_a và giả định cao trình đáy hố ga z_a bằng với cao trình đáy ống thoát z_i, có thể xác định được đường năng lượng tại hố ga (EGLₐ):

$$EGL_a = E_a + Z_a \tag{7.16}$$

BƯỚC 3: Tổn thất tại cửa ống nhập lưu

BƯỚC 3: Tổn thất thoát dòng tại ống vào

Bước cuối cùng là tính toán đường năng lượng (energy gradeline) mỗi ống vào. Phương pháp của FHWA xem xét hai trường hợp: (1) ống vào dạng plunging và (2) ống vào không plunging.

Ống vào không plunging – không có dòng chảy rơi:

Trường hợp đầu tiên là đối với các ống vào không plunging, tức là các ống có kết nối thủy lực với nước trong hố ga. Các ống vào hoạt động trong điều kiện này khi đường năng lượng tại hố ga E_a lớn hơn cao trình đáy ống vào Z_o. Trong trường hợp này, cột năng lượng tại ống vào EGL_o được tính như sau:

$$EGL_o = EGL_a + H_o \tag{7.17}$$

trong đó:
    H_o = tổn thất thoát dòng tại ống vào, tính theo Phương trình 7.18

Tổn thất thoát dòng được tính theo cách truyền thống, sử dụng cột vận tốc tại ống vào vì không có điều kiện dòng siêu tới hạn (supercritical) tại ống vào. Phương trình như sau:

$$H_o = K_o \cdot \left( \frac{V^2}{2g} \right) \tag{7.18}$$

trong đó:
    K_o = hệ số tổn thất thoát dòng = 0.4, không thứ nguyên

Ống vào dạng plunging – có dòng chảy rơi

Trường hợp thứ hai là đối với ống vào có dòng chảy đổ từ cao xuống (plunging). Với các ống dạng plunging, đường năng lượng tại ống vào EGL_o được lấy là đường năng lượng được tính từ thủy lực tại ống vào. EGL_o trong trường hợp này không phụ thuộc vào mực nước hoặc tổn thất tại hố ga.

Tiếp tục tính toán ngược dòng

Dù là trường hợp không plunging hay plunging, đường năng lượng thu được sẽ được dùng để tiếp tục tính toán ngược dòng đến hố ga kế tiếp. Quy trình ba bước bao gồm:
(1) ước tính tổn thất đầu vào,
(2) tổn thất bổ sung,
(3) tổn thất thoát dòng,
sẽ được lặp lại tại mỗi hố ga.

Việc áp dụng quy trình này được trình bày trong ví dụ thiết kế hệ thống thoát nước mưa ở Chương 8 (Ví dụ 8.1).