Hiện tượng nhảy thủy lực là một hiện tượng tự nhiên xảy ra khi dòng chảy siêu tới hạn bị buộc phải chuyển sang dòng chảy dưới tới hạn do gặp vật cản trong dòng chảy. Sự thay đổi đột ngột trong điều kiện dòng chảy này đi kèm với nhiễu loạn đáng kể và sự mất năng lượng. Hiện tượng nhảy thủy lực có thể được minh họa bằng sơ đồ năng lượng riêng như thể hiện trong Hình 6.1. Dòng chảy đi vào vùng nhảy tại vận tốc siêu tới hạn \(V_1\) và độ sâu \(y_1\), với năng lượng riêng là \(E = y_1 + V_1^2/(2g)\). Thành phần năng lượng chiếm ưu thế là động năng \(V_1^2/(2g)\). Khi chiều sâu dòng chảy tăng lên qua vùng nhảy, năng lượng riêng giảm dần. Dòng chảy rời khỏi vùng nhảy ở trạng thái dưới tới hạn, và lúc này thế năng (độ sâu y) chiếm ưu thế.
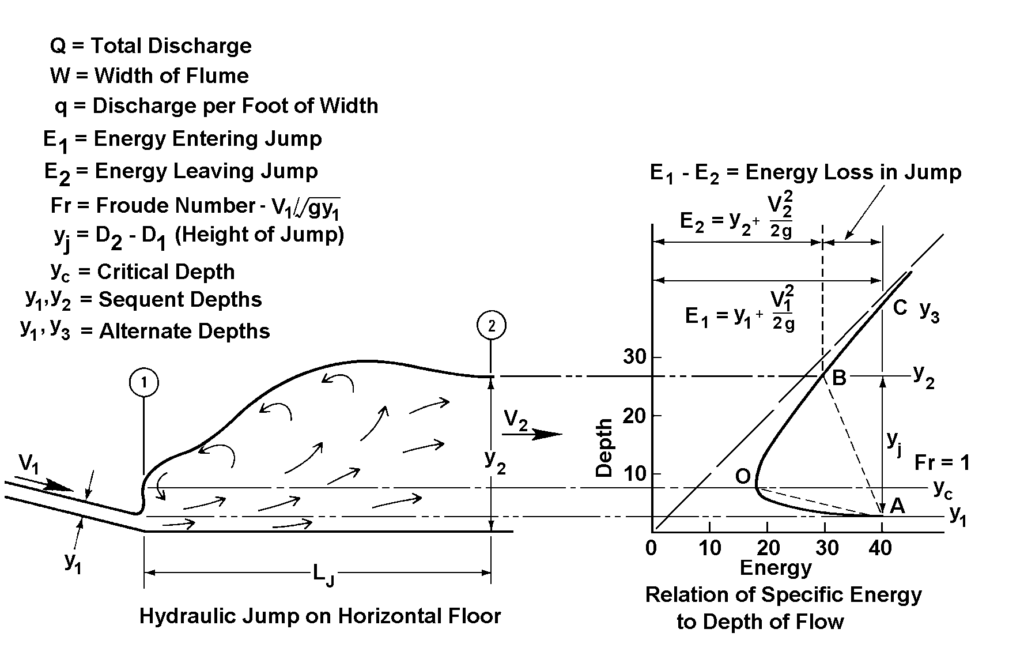
Ghi chú trong hình:
- Q = Tổng lưu lượng
- W = Bề rộng máng
- q = Lưu lượng trên một đơn vị bề rộng
- \(E_1\) = Năng lượng trước nhảy
- \(E_2\) = Năng lượng sau nhảy
- Fr = Số Froude trước nhảy
- \(y_j = D_2 – D_1\) = Chiều cao của vùng nhảy
- \(y_c\) = Độ sâu tới hạn
- \(y_1, y_2\) = Độ sâu sequent
- \(y_1, y_3\) = Độ sâu alternat
(nd: \(y_1, y_2\) và \(y_3\))
Trong hiện tượng nhảy thủy lực, các ký hiệu \(y_2\) và \(y_3\) đều liên quan đến độ sâu dòng chảy, nhưng có ý nghĩa khác nhau trong sơ đồ năng lượng.
\(y_2\) – Sequent Depth (độ sâu sau nhảy):
- Đây là độ sâu của dòng chảy sau nhảy thủy lực, ứng với dòng chảy dưới tới hạn.
- Nó là độ sâu sequent tương ứng với một độ sâu đầu vào \(y_1\) (trước nhảy) trong cùng một giá trị năng lượng riêng.
- \(y_2\) luôn lớn hơn \(y_1\) trong nhảy thủy lực.
- Được tính từ phương trình liên hệ giữa \(y_1, y_2\), và số Froude Fr.
Trong hình, \(y_2\) nằm trên đoạn BC (trên trục tung), nơi dòng chảy đã mất động năng và chuyển sang thế năng chiếm ưu thế
\(y_3\) – Alternate Depth (độ sâu tương đương năng lượng):
- Là độ sâu khác cũng cho cùng một năng lượng riêng E, nhưng không nhất thiết liên quan đến nhảy thủy lực.
- Với một giá trị năng lượng riêng cho trước, tồn tại hai độ sâu dòng chảy:
- Một độ sâu nhỏ (dòng siêu tới hạn),
- Một độ sâu lớn hơn (dòng dưới tới hạn).
- Chúng được gọi là alternate depths (độ sâu thay thế lẫn nhau), ký hiệu thường là \(y_1 và y_3.\)
Trong hình, \(y_3\) nằm bên phải điểm O (trên trục tung), cùng năng lượng với \(y_1\), nhưng thuộc dòng dưới tới hạn.
Tóm tắt so sánh:
| Ký hiệu | Tên gọi | Ý nghĩa | Liên quan đến nhảy thủy lực? |
|---|---|---|---|
| /(y_2/) | Sequent depth | Độ sâu dòng chảy sau nhảy | ✅ Có (rất quan trọng) |
| /(y_3/) | Alternate depth | Độ sâu khác cùng năng lượng với \(y_1\) | ❌ Không nhất thiết |
Bạn có thể hiểu đơn giản:
\(y_3\) → độ sâu thay thế ứng với \(y_1\) theo đường cong năng lượng, không phải luôn là \(y_2\)
\(y_1\) → trước nhảy (dòng siêu tới hạn)
\(y_2\) → sau nhảy (dòng dưới tới hạn)
6.1 Các loại nhảy thủy lực
Khi số Froude ở thượng lưu Fr=1.0, dòng chảy là tới hạn và không thể hình thành nhảy thủy lực.
Với các giá trị Fr > 1.0, nhưng nhỏ hơn 1.7, dòng chảy thượng lưu chỉ hơi vượt quá độ sâu tới hạn, và sự chuyển từ dòng siêu tới hạn sang dòng dưới tới hạn chỉ tạo ra một nhiễu loạn nhỏ trên mặt nước. Ở giới hạn cao của khoảng này, khi Fr tiệm cận 1.7, độ sâu hạ lưu sẽ vào khoảng gấp đôi độ sâu đầu vào và vận tốc đầu ra xấp xỉ bằng một nửa vận tốc đầu vào.
Cục Khai hoang Hoa Kỳ (USBR, 1987) đã xác định mối quan hệ giữa hình thái nhảy thủy lực và đặc điểm dòng chảy theo số Froude đối với các giá trị Fr > 1.7, như minh họa trong Hình 6.2.
Khi số Froude nằm trong khoảng từ 1.7 đến 2.5, bắt đầu xuất hiện vùng xoáy (roller), và vùng này trở nên mạnh hơn khi Fr tăng. Đây là loại nhảy thủy lực sơ khởi (prejump) với mức mất năng lượng thấp. Nước chảy khá êm, vận tốc phân bố đều qua tiết diện dòng và mức tổn thất năng lượng nằm trong khoảng 20%.
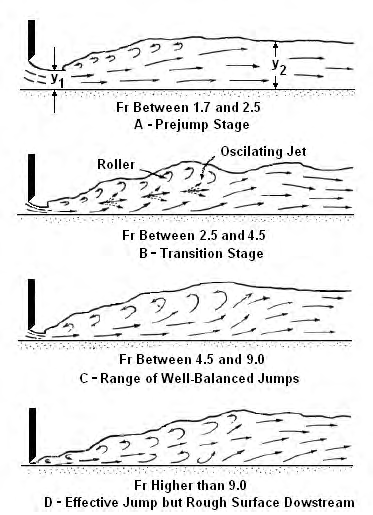
Một dạng nhảy dao động xảy ra khi số Froude nằm trong khoảng từ 2.5 đến 4.5. Dòng tia vào luân phiên chảy sát đáy và rồi dọc theo mặt nước. Điều này gây ra sóng mặt không mong muốn, có thể dẫn đến các vấn đề xói lở ở hạ lưu vùng nhảy.
Một nhảy cân bằng và ổn định xảy ra khi số Froude của dòng vào lớn hơn 4.5. Sự nhiễu loạn của chất lỏng chủ yếu giới hạn trong vùng nhảy, và với các số Froude lên đến 9.0, mặt nước hạ lưu tương đối êm. Có thể kỳ vọng mức tổn thất năng lượng trong nhảy thủy lực từ 45 đến 70 phần trăm.
Với số Froude lớn hơn 9.0, hiện tượng nhảy thủy lực diễn ra rất hiệu quả nhưng mặt nước gồ ghề có thể gây ra các vấn đề xói lở ở hạ lưu.
Hiện tượng nhảy thủy lực thường xảy ra trong điều kiện dòng chảy tự nhiên, và với thiết kế phù hợp, có thể là một phương tiện hiệu quả để tiêu tán năng lượng tại các công trình thủy lực. Các biểu thức dùng để tính tỷ số độ sâu trước và sau nhảy (độ sâu sequent) và chiều dài nhảy là cần thiết để thiết kế các cấu trúc tiêu năng gây ra nhảy thủy lực. Các biểu thức này liên quan đến số Froude tại cửa ra cống, vốn đối với nhiều cống thường nằm trong khoảng từ 1.5 đến 4.5.
6.2 Nhảy thủy lực trong kênh horizontal
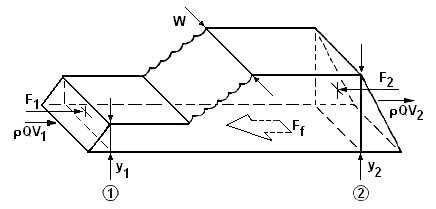
Hiện tượng nhảy thủy lực trong bất kỳ hình dạng kênh horizoltal nào đều tương đối dễ phân tích (Sylvester, 1964). Hình 6.3 minh họa thể tích kiểm soát được sử dụng và các lực liên quan.
Tiết diện điều khiển 1 là trước nhảy, nơi dòng chảy chưa bị rối loạn, và tiết diện điều khiển 2 là sau nhảy, đủ xa về phía hạ lưu để dòng chảy được xem là song song trở lại. Phân bố áp suất trong cả hai tiết diện được giả định là thủy tĩnh.
Sự thay đổi động lượng của dòng vào và ra được cân bằng bởi tổng lực tác động lên thể tích kiểm soát, tức là lực áp và lực ma sát biên. Vì chiều dài nhảy tương đối ngắn, nên tổn thất năng lượng bên ngoài (do lực ma sát biên) có thể được bỏ qua mà không gây sai số đáng kể. Ngoài ra, kênh có thể được coi là horizontal với độ dốc đến 18% (góc 10 độ so với phương nằm ngang) mà không gây sai số nghiêm trọng.
Phương trình động lượng cho phép giải được độ sâu sequent \(y_2\) và vận tốc hạ lưu \(V_2\). Khi hai giá trị này đã biết, tổn thất năng lượng bên trong và hiệu suất của nhảy có thể xác định được bằng cách áp dụng phương trình năng lượng.
Dạng tổng quát của phương trình động lượng có thể được sử dụng để giải bài toán mối quan hệ sequent-depth trong bất kỳ hình dạng kênh nào có đáy horizontal. Định nghĩa đại lượng động lượng như sau: $$M = \frac{Q^2}{gA} + A Y$$
và nhận thấy rằng động lượng được bảo toàn qua hiện tượng nhảy thủy lực, ta có thể viết:
$$\frac{Q^2}{gA_1} + A_1 Y_1 = \frac{Q^2}{gA_2} + A_2 Y_2 \tag{6.1}$$
trong đó:
- Q = lưu lượng dòng chảy qua kênh, m³/s (ft³/s)
- \(A_1, A_2\) = diện tích mặt cắt ngang tại các tiết diện 1 và 2, m² (ft²)
- \(Y_1, Y_2\) = khoảng cách từ mặt nước đến trọng tâm mặt cắt ngang, m (ft)
Độ sâu từ mặt nước đến trọng tâm mặt cắt ngang có thể được biểu diễn dưới dạng hàm của hình dạng kênh và độ sâu lớn nhất: Y=Ky
Trong đó, K là một hệ số đại diện cho hình dạng mặt cắt của kênh, còn y là độ sâu tối đa trong kênh. Thay đại lượng này vào Phương trình (6.1) và biến đổi lại, ta thu được:
$$A_1 K_1 y_1 – A_2 K_2 y_2 = \left(\frac{1}{A_2} – \frac{1}{A_1}\right)\frac{Q^2}{g}$$
Biến đổi và sử dụng \(Fr_1^2 = \frac{V_1^2}{g y_1} = \frac{Q^2}{A_1^2 g y_1}\)
ta được:
$$A_1 K_1 y_1 – A_2 K_2 y_2 = Fr_1^2 \cdot A_1 y_1 \left(\frac{A_1}{A_2} – 1\right)$$
Chia hai vế cho \(A_1 y_1\), ta thu được:
$$\frac{K_2 A_2 y_2}{A_1 y_1} – K_1 = Fr_1^2 \left(1 – \frac{A_1}{A_2}\right) \tag{6.2}$$
Đây là một biểu thức tổng quát cho cú nhảy thủy lực trong kênh horizoltal. Các hằng số \(K_1, K_2\) và tỉ số \(A_1/A_2\) đã được xác định cho các mặt cắt hình chữ nhật, tam giác, parabol, tròn, thang và các dạng hình học khác bởi Sylvester (1964). Các mối quan hệ cho mặt cắt hình chữ nhật và hình tròn sẽ được trình bày trong các phần sau.
6.2.1 Kênh hình chữ nhật (Rectangular Channels)
Đối với kênh hình chữ nhật, thay \(K_1 = K_2 = 1/2\) và \(A_1 / A_2 = y_1 / y_2\) vào Phương trình 6.2, ta được biểu thức:
$$\frac{y_2^2}{y_1^2} – 1 = 2 Fr_1^2 \left( 1 – \frac{y_1}{y_2} \right)$$
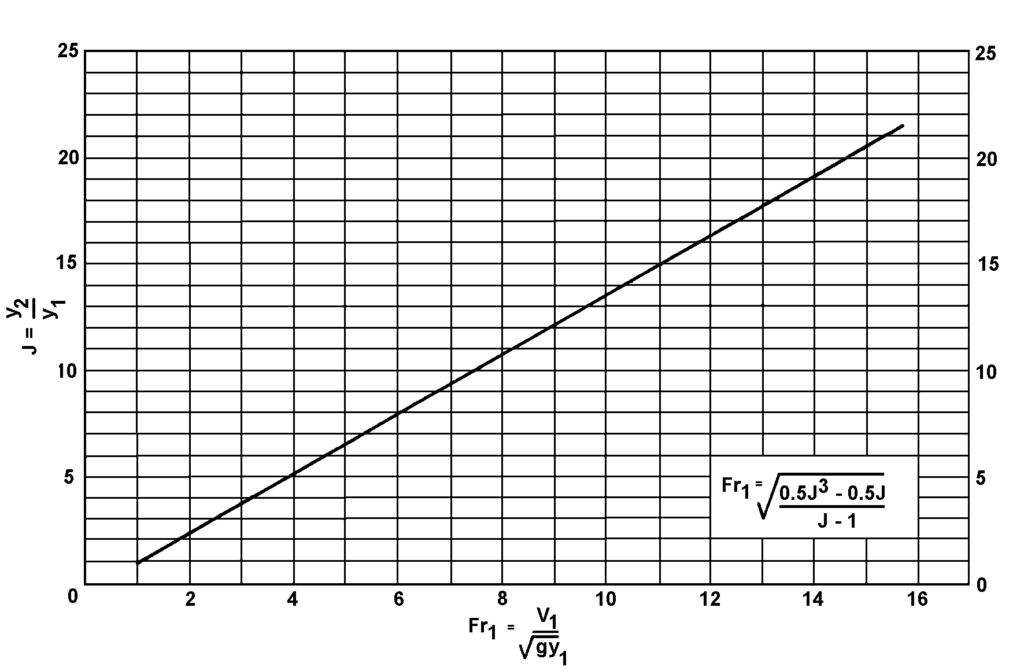
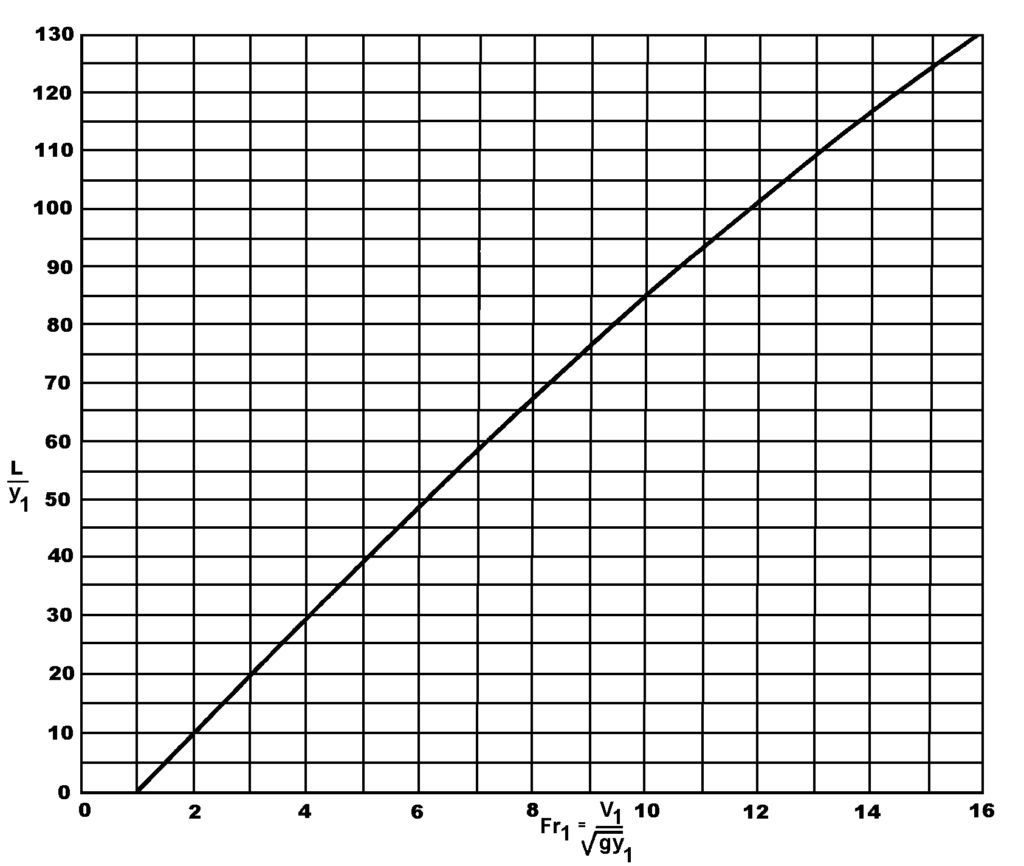
Nếu đặt \(y_2 / y_1 = J\), thì biểu thức cho cú nhảy thủy lực trong kênh horizoltal, hình chữ nhật trở thành Phương trình 6.3, được biểu diễn trong Hình 6.4:
$$J^2 – 1 = 2 Fr_1^2 \left(1 – \frac{1}{J} \right) \tag{6.3}$$
Chiều dài nhảy thủy lực có thể được xác định từ Hình 6.5. Chiều dài nhảy được đo đến tiết diện hạ lưu nơi mà mặt nước trung bình đạt đến độ sâu lớn nhất và trở nên tương đối bằng phẳng. Có thể xảy ra sai số khi xác định chiều dài vì mặt nước thường khá phẳng ở cuối vùng nhảy. Đây là một trong những lý do có rất nhiều công thức thực nghiệm khác nhau để xác định chiều dài nhảy được nêu trong tài liệu. Chiều dài nhảy trong bể hình chữ nhật đã được nghiên cứu rất kỹ lưỡng.
Thiết kế bể tiêu năng là một ứng dụng phổ biến cho cú nhảy thủy lực trong kênh hình chữ nhật (xem Chương 8). Các bể nhảy tự do có thể được thiết kế cho bất kỳ điều kiện dòng chảy nào; nhưng vì lý do kinh tế và hiệu suất, chúng thường chỉ được sử dụng trong vùng số Froude thấp.
- Dòng chảy với số Froude nhỏ hơn 1.7 có thể không cần bể tiêu năng, nhưng có thể cần bảo vệ bằng đá lát (riprap) hoặc tường chắn.
- Với số Froude từ 1.7 đến 2.5, chỉ cần bể nhảy tự do là đủ. Trong khoảng này, tổn thất năng lượng dưới 20%; conjugate depth (độ sâu liên hợp) gấp khoảng 3 lần độ sâu dòng vào; và chiều dài bể cần thiết nhỏ hơn 5 lần độ sâu liên hợp.
Nhiều cống trên đường bộ hoạt động trong vùng Froude này.
Ở các số Froude cao hơn, việc sử dụng baffles (tấm chắn) và sills (ngưỡng tràn) có thể giúp giảm chiều dài bể và ổn định nhảy nước trên phạm vi điều kiện dòng chảy rộng hơn.
Ví dụ thiết kế: Cú nhảy thủy lực trong kênh hình chữ nhật horizontal (hệ SI)
Xác định chiều cao và chiều dài của cú nhảy thủy lực trong một cống hộp rộng 2.134 m. Đồng thời, ước tính phạm vi lưu lượng mà tại đó cú nhảy thủy lực sẽ xảy ra khi xả vào một kênh hình thang.
Cho:
- S = 0.2%
- \(Q = 11.33\ \text{m}^3/\text{s}\)
- \(V_1 = 5.79\ \text{m/s}\)
- \(y_1 = 0.914\ \text{m}\)
- Fr = 1.9
Kênh hình thang:
- B = 3.04m
- Độ dốc mái: 1V:2H
- n = 0.03
- S = 0.04%
Giải
Bước 1. Tìm độ sâu liên hợp (conjugate depth) từ Hình 6.4.
$$J = y_2 / y_1 = 2.2$$
$$y_2 = 2.2(0.914) = 2.011 \, m$$
Bước 2. Tìm chiều dài của cú nhảy từ Hình 6.5
$$L / y_1 = 9.0$$
$$L = 0.914(9.0) = 8.226 \, m$$
Bước 3. Tính vận tốc sau nhảy
$$V_2 = Q / A_2 = 11.33 / [2.134(2.011)] = 2.64 \, m/s$$
Giảm vận tốc = (5.79 – 2.64) / 5.79 = 54.4%
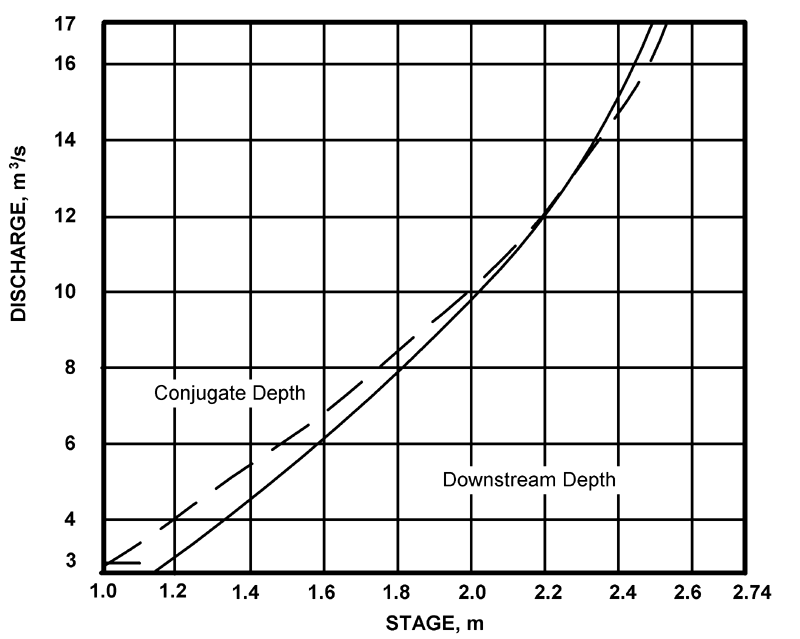
Bước 4. Xây dựng đường cong Q so với mực nước cho kênh hình thang hạ lưu bằng cách sử dụng HDS Số 3 (FHWA, 1961) hoặc Bảng B.1 để xác định mối quan hệ với conjugate depth (xem bên dưới).
Bước 5. Xem xét yêu cầu về sequent depth (độ sâu sequent). Biểu đồ cho thấy rằng có đủ độ sâu tailwater trong kênh hạ lưu cho các lưu lượng lên đến khoảng 13.6 m³/s.
Với lưu lượng lớn hơn, cú nhảy thủy lực sẽ bắt đầu di chuyển xuống hạ lưu.
Giả định trong ví dụ này là độ sâu normal trong kênh hạ lưu sẽ đạt được ngay khi dòng chảy ra khỏi cống. Trong trường hợp thực tế, một bể tiêu năng (xem Mục 8.1) thường cần thiết để tạo đủ độ sâu tailwater nhằm gây ra cú nhảy thủy lực, hoặc cống cần được thiết kế dưới dạng cống gãy khúc (xem Chương 7).
6.2.2 Kênh hình tròn (Circular Channels)
Kênh hình tròn được chia thành hai trường hợp: khi \(y_2\) lớn hơn đường kính D, và khi \(y_2\) nhỏ hơn D.
Đối với \(y_2\) nhỏ hơn D: $$(K_2 \cdot y_2 \cdot C_2 / (y_1 C_1)) – K_1 = Fr_1^2 \left(1 – \frac{C_1}{C_2} \right) \tag{6.4}$$
Đối với \(y_2\) lớn hơn hoặc bằng D: $$(y_2 C_2 / (y_1 C_1)) – 0.5 \cdot (C_2 D / (C_1 y_1)) – K_1 = Fr_1^2 \left(1 – \frac{C_1}{C_2} \right) \tag{6.5}$$
Các hệ số C và K là hàm của y/D và có thể được tra từ Bảng 6.1.
Bảng 6.1. Các hệ số cho kênh nằm ngang, hình tròn
| Y/D | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 |
|---|---|---|---|---|---|---|---|---|---|---|
| K | 0.410 | 0.413 | 0.416 | 0.419 | 0.424 | 0.432 | 0.445 | 0.462 | 0.473 | 0.500 |
| C | 0.041 | 0.112 | 0.198 | 0.293 | 0.393 | 0.494 | 0.587 | 0.674 | 0.745 | 0.748 |
| C′ | 0.600 | 0.800 | 0.917 | 0.980 | 1.000 | 0.980 | 0.917 | 0.800 | 0.600 | 0.600 |
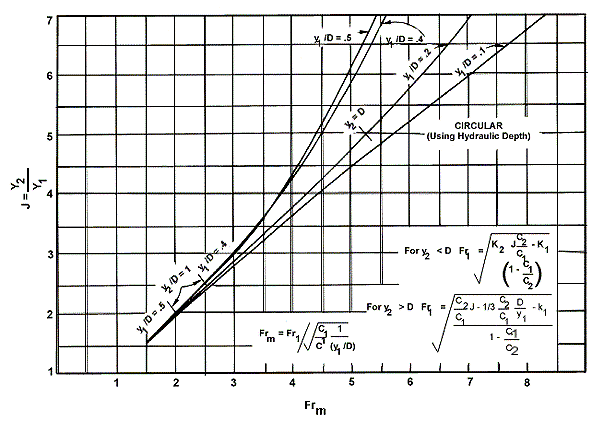
Trong Phương trình 6.4 và 6.5, \(Fr_1\) được tính dựa trên độ sâu lớn nhất trong kênh. Hình 6.6 có thể được sử dụng thay thế các phương trình này.
Ngoài ra, kỹ sư thiết kế có thể tính số Froude dựa trên độ sâu thủy lực, \(Fr_m = V / \sqrt{g y_m}\)
trong đó \(y_m = (C/C’)D\) hoặc \(y_m = A / T.\)
- Với biểu thức đầu tiên, giá trị C′ được tra từ Bảng 6.1.
- Với biểu thức thứ hai, A là diện tích tiết diện dòng chảy và T là bề rộng mặt nước.
Hình 6.7 là biểu đồ thiết kế cho kênh horizontal, hình tròn sử dụng độ sâu thủy lực để tính số Froude.
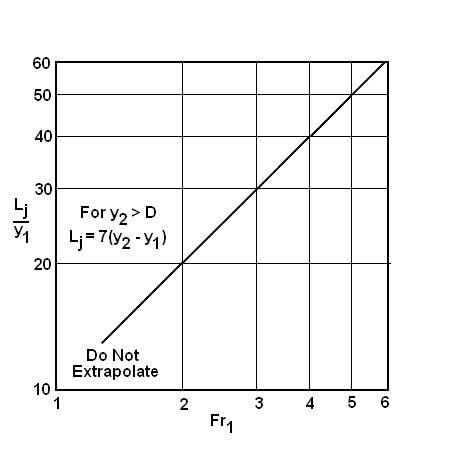
Chiều dài nhảy thủy lực thường được đo đến tiết diện hạ lưu nơi mặt nước đạt độ sâu cực đại và trở nên tương đối bằng phẳng. Đường cong chiều dài nhảy trong kênh tròn được xác định bằng Hình 6.8, áp dụng cho trường hợp \(y_2 < D.\)
Đối với trường hợp \(y_2 > D\), chiều dài nên lấy bằng 7 lần hiệu độ sâu: \(L_J = 7(y_2 – y_1)\)

Ví dụ thiết kế: Cú nhảy thủy lực trong kênh hình tròn horizontal (hệ SI)
Xác định chiều cao và chiều dài của cú nhảy thủy lực trong một cống RCP có đường kính 2.134 m.
Cho:
- S = 2%
- \(Q = 5.664\ \text{m}^3/\text{s}\)
- \(V_1 = 5.182\ \text{m/s}\)
- \(y_1 = 0.732\ \text{m}\)
- \(Fr_1 = 1.9\)
Giải
Bước 1. Tìm conjugate depth (độ sâu liên hợp) trong kênh hình tròn.
$$y_1 / D = 0.732 / 2.134 = 0.34 \, (\text{dùng 0.4})$$
$$J = y_2 / y_1 = 2.3 \, \text{từ Hình 6.6}$$
$$y_2 = 2.3 (0.732) = 1.684 \, m \quad \text{và} \quad y_2 / D = 0.78 \, (\text{dùng 0.8})$$
(Sử dụng Phương trình 6.4 với \(C_1 = 0.293, K_1 = 0.419, C_2 = 0.674, K_2 = 0.462 \) cũng cho kết quả tương tự.)
Bước 2. Tìm chiều dài nhảy từ Hình 6.8
$$L_j / y_1 = 19$$
$$L_j = 0.732 \cdot 19 = 13.9 \, m$$
Bước 3. Tính vận tốc sau nhảy
Với \(y_2 / D = 0.78\), ta có \(A / D^2 = 0.6573\) từ Bảng 3.3 và \(A = 2.99 \, m^2\) \(V_2 = Q / A_2 = 5.664 / 2.99 = 1.89 \, m/s\)
Giảm vận tốc: (5.182 – 1.89)/5.182 = 63.5%
6.2.3 Hiệu suất cú nhảy thủy lực
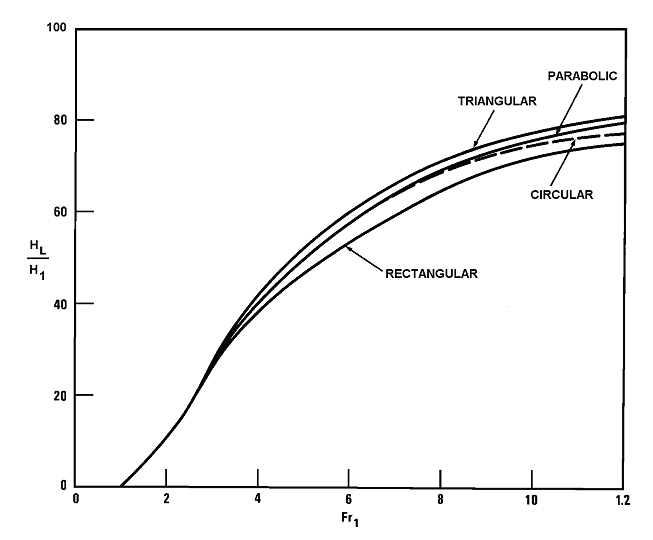
Một biểu thức tổng quát cho tổn thất năng lượng \((H_L / H_1)\) trong bất kỳ hình dạng kênh nào là:
$$\frac{H_L}{H_1} = 2 – 2(y_2) + Fr_m^2 \left[1 – \frac{A_1^2}{A_2^2} \right] / (2 + Fr^2) \tag{6.6}$$
trong đó:
- \(Fr_m\) = Số Froude thượng lưu tại tiết diện 1,
\(Fr_m^2 = \frac{V^2}{g y_m}\) - \(y_m\) = độ sâu thủy lực, m (ft)
Biểu thức này được biểu diễn trên biểu đồ cho các hình dạng kênh khác nhau như trong Hình 6.9.
Mặc dù Hình 6.9 cho thấy rằng các tiết diện không hình chữ nhật hiệu quả hơn ở các giá trị số Froude cao, cần lưu ý rằng các tiết diện này cũng liên quan đến:
- Nhảy thủy lực dài hơn
- Vấn đề về ổn định
- Mặt nước hạ lưu gồ ghề hơn
6.3 Nhảy thủy lực trong kênh dốc
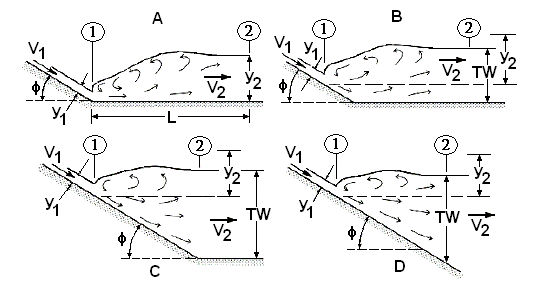
Hình 6.10 (Bradley, 1961) chỉ ra một phương pháp xác định ranh giới nhảy thủy lực trong các kênh nằm ngang (horizontal) và kênh dốc (sloping). Các kênh horizontal (trường hợp A) đã được trình bày ở phần trước. Các kênh dốc sẽ được thảo luận trong mục này. Nếu đáy kênh được chọn làm mốc, phương trình động lượng trở thành:
$$\frac{Q(V_2 – V_1)}{g} = 0.5B(y_1^2 – y_2^2) \cos \phi + \frac{w(\sin \phi)}{\gamma} \tag{6.7}$$
trong đó,
- \(\gamma\) = trọng lượng riêng của nước, N/m³ (lb/ft³)
- \(\phi\) = góc giữa kênh và mặt ngang
- B = bề rộng đáy kênh (kênh chữ nhật), m (ft)
- w = trọng lượng của khối nước trong vùng nhảy, N (lb)
Phương trình động lượng dùng cho kênh horizontal không thể được áp dụng trực tiếp cho nhảy thủy lực trong kênh dốc vì phải xem xét đến trọng lượng của khối nước trong vùng nhảy. Khó khăn phát sinh trong việc xác định mặt cắt mặt nước để tính thể tích nước trong vùng nhảy ứng với các độ dốc kênh khác nhau. Thể tích này có thể được bỏ qua nếu độ dốc nhỏ hơn 10% và nhảy thủy lực được phân tích như kênh horizontal.
Cục Khai hoang Hoa Kỳ (Bradley, 1961) đã thực hiện các thí nghiệm mô hình quy mô lớn đối với các nhảy thủy lực kiểu B và C để xác định mối quan hệ giữa chiều dài và độ sâu nhảy. Tài liệu này nên được tham khảo nếu nhảy thủy lực trong kênh chữ nhật dốc đang được xem xét. Các thí nghiệm mô hình nên được thực hiện nếu các dạng kênh khác đang được xem xét.
Hỗ trợ duy trì trang:
Tôi xây dựng trang này để chia sẻ các tài liệu kỹ thuật cốt lõi trong thiết kế hạ tầng giao thông.
Nếu bạn thấy nội dung hữu ích và muốn góp phần duy trì trang hoạt động bền vững, tôi rất trân trọng mọi sự ủng hộ.