Trong các trường hợp không có đủ hành lang để bố trí cấu trúc tiêu năng bên ngoài tại điểm xả của cống hoặc máng xối, có một số lựa chọn cho các cấu trúc tiêu năng bên trong hoặc tích hợp, bao gồm việc bổ sung các phần tử gồ bên trong suốt chiều dài cống hoặc máng, hoặc chỉ ở gần cửa xả. Những phương pháp này có thể áp dụng cho các ống cống kín (kiểu thông thường hoặc gãy khúc) cũng như trong các máng hở, thường là hình chữ nhật.
Các phần tử gồ đôi khi là một phương pháp tiện lợi để kiểm soát vận tốc dòng chảy tại cửa xả đối với các công trình cống mà thân (barrel) cống không được sử dụng hết công suất vì đang làm việc ở chế độ inlet control. Các phần tử gồ này có thể được thiết kế để làm giảm vận tốc trong cống, bao gồm, ở giới hạn, tạo ra dòng chảy kiểu cuộn (tumbling flow), trong đó vận tốc tại cửa xả được giảm xuống tới vận tốc tới hạn. Các phần tử gồ bên trong như vậy có thể được đặt dọc theo toàn bộ chiều dài của cống hoặc máng, hoặc chỉ ở khu vực gần cửa xả, tùy thuộc vào điều kiện thủy lực và điều kiện đầu ra mong muốn.
Chương này trình bày một loạt các chiến lược nhằm tăng độ gồ ghề bao gồm dòng chảy cuộn, tăng sức cản, USBR Type IX baffled apron (dốc nước có gồ), đoạn runout của cống gãy khúc, outlet weirs (cửa xả có ngưỡng tràn), và outlet drop/weirs (cửa xả kết hợp bậc/ngưỡng tràn). Tính phù hợp và các giới hạn của chúng sẽ được trình bày trong các phần sau.
7.1 Tumbling Flow (Dòng chảy cuộn)
Các phần tử gồ đặt bên trong lòng cống hoặc máng hở có thể được sử dụng để giảm vận tốc bằng cách tạo ra một chuỗi các cú nhảy thủy lực trong một hiện tượng gọi là dòng chảy cuộn (Peterson và Mohanty, 1960). Dòng chảy cuộn là một cấu trúc tiêu năng tối ưu trên các dốc lớn. Về bản chất, nó là một chuỗi các cú nhảy thủy lực và đổ tràn duy trì hướng dòng chảy chủ yếu ở gần vận tốc tới hạn, ngay cả trên các độ dốc mà thông thường sẽ đặc trưng bởi vận tốc siêu tới hạn.
Một mối quan ngại lớn với dòng chảy cuộn là phù sa có thể tích tụ phía trước các phần tử gồ và làm chúng mất hiệu quả. Tuy nhiên, điều này có thể không đáng lo vì các phần tử này làm tăng khả năng vận chuyển bùn cát và có xu hướng tự làm sạch. Trong danh sách ứng dụng ban đầu của mình, Peterson và Mohanty (1960) đã lưu ý rằng:
“Bằng cách sử dụng các phần tử gồ để tạo ra nhiễu loạn lớn hơn, khả năng vận chuyển bùn cát của kênh có thể được gia tăng.”
Dòng chảy cuộn là dòng chảy theo chu kỳ, với các mẫu hình độ sâu và vận tốc được lặp lại tại mỗi phần tử gồ. Không cần phải lót toàn bộ chiều dài cống bằng các phần tử gồ để kiểm soát vận tốc đầu ra. Năm hàng phần tử gồ là đủ để thiết lập mẫu dòng chảy đều theo chu kỳ.
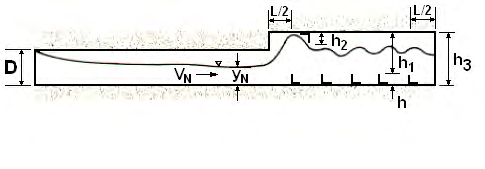
Giả thuyết cơ bản của chế độ dòng chảy tumbling là nó sẽ duy trì gần như dòng tới hạn ngay cả trên các độ dốc rất lớn. Phần tử cuối cùng được đặt tại một khoảng cách L/2 về phía thượng lưu của miệng xả để dòng chảy tái gắn vào đáy kênh đúng tại cửa xả. Phần tử đầu tiên trong đoạn mở rộng, như minh họa trong Hình 7.1, cũng nên được đặt tại một khoảng cách L/2 về phía hạ lưu kể từ điểm bắt đầu của đoạn mở rộng. Khoảng cách L/2 cho cả phần tử đầu và cuối nên được xem là giá trị tối thiểu. Kích thước và khoảng cách các phần tử gồ sẽ được mô tả trong các phần sau. Vận tốc tại cửa xả sẽ tiến gần vận tốc tới hạn, trừ khi có nước dâng phía hạ lưu. Không phải là điều bất hợp lý khi kỳ vọng cần phải nâng cao thêm độ cao cống trong vùng có tạo gồ như minh họa trong Hình 7.1.
Quy trình thiết kế dòng chảy tumbling trong các cống hộp và cống tròn có thể được tóm tắt theo các bước sau:
Bước 1. Xác minh rằng cống đang làm việc ở chế độ inlet control.
Bước 2. Tính toán điều kiện dòng chảy normal trong cống để xác định xem điều kiện xả tại cửa ra có cần được xử lý hay không.
Bước 3. Tính toán độ sâu và vận tốc tới hạn. Nếu vận tốc tới hạn nhỏ hơn hoặc bằng vận tốc xả mong muốn, thì dòng chảy cuộn có thể là một phương án tiêu năng phù hợp.
Bước 4. Xác định kích thước chiều cao phần tử, khoảng cách giữa các phần tử và các đặc điểm thiết kế khác. Chi tiết thiết kế sẽ khác nhau giữa cống hộp và cống tròn, và sẽ được trình bày trong các phần tiếp theo.
7.1.1 Dòng Chảy Tumbling Trong Cống Hộp/Máng
Hiện tượng dòng chảy tumbling đã được nghiên cứu như một phương pháp tiêu năng trong các cống hộp và máng tại Viện Bách khoa Virginia (VPI) (Morris, 1968; Morris, 1969; Mohanty, 1959). Các độ dốc lên tới 20% đã được thử nghiệm tại VPI và lên đến 35% trong các thử nghiệm tiếp theo của Cục Quản lý Đường cao tốc Liên bang (Jones, 1975).
Các máng tiêu nước trên các đoạn đào và đắp của đường giao thông là những vị trí thích hợp để áp dụng phần tử gồ như một phương pháp tiêu năng. Việc sử dụng các phần tử gồ là hợp lý đối với các độ dốc lên tới 10 hoặc 15 phần trăm. Vượt quá mức này, sự phân tách dòng và quỹ đạo dòng chảy rời khỏi đáy kênh trở nên quá lớn, cần phải có các biện pháp để hạn chế văng nước.
Một trong những hạn chế chính của dòng chảy cuộn khi dùng làm cấu trúc tiêu năng là chiều cao yêu cầu của phần tử gồ phụ thuộc chặt chẽ vào lưu lượng cho một kích thước cống cho trước. Ngược lại, chiều cao phần tử yêu cầu ít nhạy cảm hơn với độ dốc cống. Ví dụ, với cùng độ dốc và kích thước cống, nếu lưu lượng tăng gấp đôi thì chiều cao phần tử gồ cần thiết sẽ tăng khoảng 50% trong cống hộp; trong khi đó, nếu giữ nguyên lưu lượng mà tăng độ dốc từ 4% lên 8% thì chiều cao phần tử gồ chỉ tăng dưới 6%. Sẽ có nhiều trường hợp mà chiều cao phần tử phải bằng một nửa chiều cao cống để duy trì dòng chảy tumbling. Do đó, ứng dụng thực tế của dòng chảy tumbling có khả năng bị giới hạn trong các cống có lưu lượng thấp và vận tốc cao.
Dòng chảy tumbling được hình thành trong các cống hộp và máng hình chữ nhật với phần tử gồ đặt tại đáy cống như minh họa trong Hình 7.1. Độ sâu tới hạn trong cống hộp được tính từ lưu lượng đơn vị (lưu lượng chia cho bề rộng cống/máng, B).
$$y_c = \left( \frac{q^2}{g} \right)^{1/3} \tag{7.1}$$
trong đó:
- \(y_c\) = độ sâu tới hạn, m (ft)
- q = lưu lượng đơn vị (Q/B), m (ft)
Vận tốc tới hạn, chính là vận tốc tại cửa xả, có thể được xác định bằng độ sâu tới hạn và phương trình liên tục.
Dòng chảy tumbling có thể được hình thành khá nhanh bằng một trong hai cấu hình sau:
- Cấu hình thứ nhất sử dụng năm hàng phần tử gồ có cùng kích thước, như minh họa trong Hình 7.2a. Cấu hình này được khuyến nghị áp dụng cho các cống hộp.
- Cấu hình thay thế thứ hai sử dụng một phần tử đầu lớn hơn, kết hợp với bốn hàng phần tử gồ có kích thước đồng đều như trong Hình 7.2b (lưu ý rằng chỉ một phần tử gồ đồng đều được thể hiện).
Cấu hình thay thế này không được coi là giải pháp thực tiễn trong cống hộp vì kích thước phần tử đầu có thể quá lớn. Tuy nhiên, cấu hình này có thể hữu ích đối với các máng hở.

Cấu hình được khuyến nghị yêu cầu một tấm chắn bắn nước nhằm đảo ngược tia dòng chảy giữa hàng phần tử thứ nhất và thứ hai. Tấm chắn này có hiệu quả vì nó làm lệch dòng tia kiểu “đuôi gà” khỏi đáy kênh và nhanh chóng đưa dòng chảy vào trạng thái ổn định mà không cần sử dụng phần tử lớn phía trước.
Đối với cống hộp, phần trên của cống có thể đóng vai trò như tấm chắn. Tuy nhiên, nên bố trí thêm một vách hướng dòng ở phía trên để điều chỉnh hướng dòng chảy. Vách trên không nhất thiết phải có cùng kích thước với các phần tử ở đáy.
Cấu hình được khuyến nghị là sử dụng 5 hàng phần tử gồ có cùng chiều cao, với chiều cao được xác định theo công thức sau:
$$h = \frac{y_c}{(3 – 3.7 S_o)^{2/3}} \tag{7.2}$$
trong đó:
- h = chiều cao phần tử, m (ft)
- \(y_c\) = độ sâu tới hạn, m (ft)
- \(S_o\) = độ dốc cống, m/m (ft/ft)
Khoảng cách giữa các hàng phần tử gồ, ký hiệu là L, được xác định bằng tỷ lệ L/h nằm trong khoảng từ 8.5 đến 10 (bao gồm cả hai giá trị giới hạn).
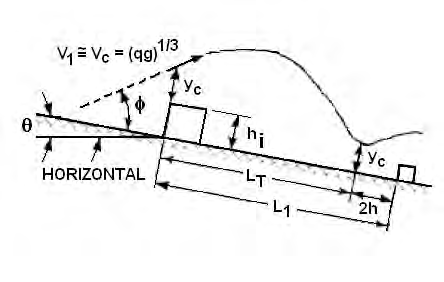
Cấu hình thay thế là sử dụng một phần tử gồ lớn phía trước, tiếp theo là bốn phần tử nhỏ hơn, như minh họa trong Hình 7.2b. Phần tử lớn ban đầu phải đáp ứng yêu cầu sau:
$$h_i > y_2 – y_c \tag{7.3}$$
trong đó:
- \(h_i\) = chiều cao phần tử đầu lớn, m (ft)
- \(y_2\) = độ sâu liên hợp cần thiết để tạo ra nhảy thủy lực, m (ft)
Độ sâu sequent \(y_2\) cần thiết cho nhảy thủy lực được tính theo công thức sau:
$$y_2 = 7.5(\text{Fr}) y_n (S_o + 0.153) \tag{7.4}$$
trong đó:
- Fr = số Froude của dòng tiếp cận tại vị trí chân cú nhảy thủy lực, không thứ nguyên
- \(y_n\) = độ sâu normal
- \(S_o\) = độ dốc cống
Phần tử đầu lớn này sẽ được theo sau bởi bốn phần tử nhỏ hơn, có chiều cao tính theo Công thức (7.2) như đã trình bày ở phần trước.
Khoảng cách giữa các phần tử nhỏ được xác định bằng cách chọn tỷ lệ L/h nằm trong khoảng từ 8.5 đến 10, như đã đề cập trước đó.
Khoảng cách \(L_1\) giữa phần tử lớn đầu tiên và phần tử nhỏ đầu tiên được tính theo công thức:
$$L_1 = 2h + 2y_c \left( \frac{\cos(\varphi – \theta)}{\cos\theta} \right) \left( \tan\theta \cos(\varphi – \theta) + \sin(\varphi – \theta) \right) \tag{7.5}$$
trong đó:
- θ = độ dốc đáy cống, đơn vị độ (xem Hình 7.2)
- φ = góc tia nước, lấy bằng 45 độ
- \(y_c\) = độ sâu tới hạn (xem Công thức 7.1), m (ft)
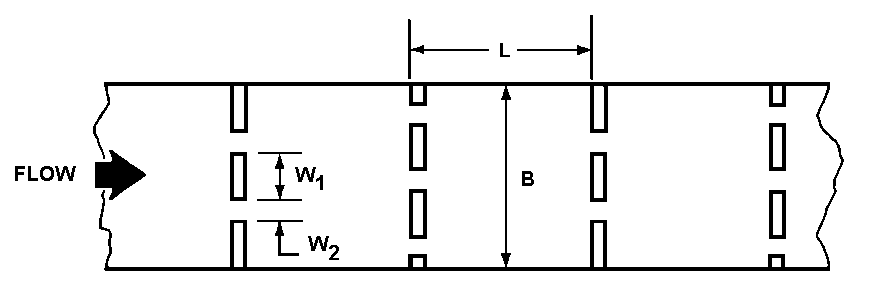
Trong cả hai cấu hình, nếu dùng các phần tử gồ liên tục chạy ngang đáy cống thì sẽ gây giữ nước và có xu hướng tích tụ bùn cát và rác. Để khắc phục điều này, có thể bố trí các khe (slots) trong các phần tử gồ như minh họa trong Hình 7.3.
Chiều rộng khe \(W_2\) được xác định theo công thức:
$$W_2 = \frac{h}{2} \tag{7.6}$$
trong đó:
- h = chiều cao của phần tử nhỏ
Chiều rộng phần tử gồ \(W_1\) sau đó được tính dựa trên chiều rộng cống và số lượng khe theo công thức:
$$W_1 = \frac{B – N_s W_2}{3} \tag{7.7}$$
trong đó:
- \(N_s\) = số lượng khe rãnh
- B = chiều rộng cống, m (ft)
Đối với hàng 1, 3 và 5, chiều rộng phần tử gồ được tính với 2 khe rãnh, còn hàng 2 và 4 thì tính với 3 khe rãnh. Cần sắp xếp xen kẽ các khe để làm rối các dòng chảy giữa các phần tử gồ, như minh họa trong Hình 7.3.
Chiều cao tia nước (Jet Height), \(h_1\):
Độ cao phần nhô lên của cống cần được kiểm tra để đảm bảo có đủ không gian cho tia nước khi dòng chảy bị phá vỡ tại các phần tử gồ. Đối với cống, tia nước nên vừa đủ chạm đến đỉnh cống.
Chiều cao tia nước được tính:
$$h_1 = 1.25\, y_c \tag{7.8}$$
Tấm chắn bắn nước (Splash Shield Height), \(h_2\):
- Nếu \(D < h_1 + h\): cần nâng cống lên một chiều cao \(h_3 = h_1 + h\)
- Nếu \(D > h_1 + h\): cần bố trí tấm chắn bắn nước với chiều cao \(h_2\) như sau:
$$h_2 = 1.5(D – (h_1 + h)) \tag{7.9}$$
Nếu \(h_2 < 50\, \text{mm}\) thì dùng giá trị mặc định là 50 mm.
Chiều dài tấm chắn bắn nước bằng nửa khoảng cách giữa các phần tử gồ (L/2), và cần bao phủ toàn bộ chiều rộng dòng chảy.
Không cần tấm chắn bắn nước nếu sử dụng phần tử gồ đầu lớn.
Ví dụ thiết kế: Dòng chảy chảy tumbling trong cống hộp bê tông (SI)
Thiết kế một cống hộp bê tông để tạo dòng chảy cuộn (tumbling flow) (xem Hình 7.2).
Xác định xem vận tốc tại cửa xả có nhỏ hơn 3 m/s hay không.
Cho:
- \(Q = 2.8\ \text{m}^3/\text{s}\)
- \(B = 1.2\ \text{m}\), chiều rộng đáy
- D = 1.2m, chiều sâu hoặc đường kính, tùy ngữ cảnh kênh hoặc cống
- n = 0.013, hệ số nhám Manning
- \(S_o = 0.06\ \text{m/m}\), độ dốc đáy kênh hoặc cống
Giải
Bước 1.
Xác minh rằng cống đang trong điều kiện khống chế ở cửa vào (inlet control).
→ Trong ví dụ này, cống đang ở điều kiện inlet control.
Bước 2.
Tính điều kiện dòng chảy normal (normal flow). Sử dụng phương pháp thử và sai với phương trình Manning:
- \(y_n = 0.342\ \text{m}\)
- \(V_n = 6.8\ \text{m/s}\)
→ Vì lớn hơn 3 m/s → cần tiêu năng.
Bước 3.
Tính độ sâu tới hạn và vận tốc tới hạn.
- Tính lưu lượng riêng (unit discharge):
\(q = \frac{Q}{B} = \frac{2.8}{1.2} = 2.333\ \text{m}^2/\text{s}\) - Dùng công thức (7.1): $$y_c = \left( \frac{q^2}{g} \right)^{1/3} = \left( \frac{2.333^2}{9.81} \right)^{1/3} = 0.822\ \text{m}$$
- Tính vận tốc tới hạn: $$V_c = \frac{Q}{y_c \cdot B} = \frac{2.8}{0.822 \cdot 1.2} = 2.8\ \text{m/s}$$
→ Vì vận tốc xả sẽ là vận tốc tới hạn, thiết kế này phù hợp với tiêu chí ≤ 3 m/s.
Bước 4.
Tính chiều cao phần tử (element height), khoảng cách dọc (L), và tấm chắn nước (splash shield).
Áp dụng quy trình đề xuất: sử dụng 5 hàng phần tử gồ có chiều cao bằng nhau.
Tính theo công thức (7.2):
$$h = \frac{y_c}{(3 – 3.7 S_o)^{2/3}} = \frac{0.822}{(3 – 3.7 \cdot 0.06)^{2/3}} = 0.42\ \text{m}$$
Tính khoảng cách dọc L:
$$L = 8.5 \cdot h = 8.5 \cdot 0.42 = 3.57\ \text{m}$$
Từ công thức (7.6) và (7.7):
Tính chiều rộng khe mở (slot width):
$$W_2 = \frac{h}{2} = \frac{0.42}{2} = 0.21\ \text{m}$$
Tính chiều rộng phần tử gồ (element width):
- Cho hàng 1, 3 và 5 (dùng 2 khe):
$$W_1 = \frac{B – N_s W_2}{3} = \frac{1.2 – 2(0.21)}{3} = 0.26\ \text{m}$$
- Cho hàng 2 và 4 (dùng 3 khe):
$$W_1 = \frac{1.2 – 3(0.21)}{3} = 0.19\ \text{m}$$
Tính chiều cao và chiều dài tấm chắn nước (splash shield):
- Chiều cao tia (jet height):
$$h_1 = 1.25 y_c = 1.25 (0.822) = 1.03\ \text{m}$$
$$h_1 + h = 1.03 + 0.42 = 1.45\ \text{m}$$
Do chiều cao cống hiện tại chỉ 1.2 m < 1.45 m, cần mở rộng tiết diện đến 1.45 m.
- Dùng công thức (7.9) tính chiều cao tấm chắn nước:
$$h_2 = 1.5 (D – (h_1 + h)) = 1.5 (1.5 – 1.45) = 0.075\ \text{m}$$
Chọn \(h_2 = 0.075\ \text{m}\) (vì > giá trị tối thiểu 0.05 m)
- Chiều dài tấm chắn nước:
$$L_\text{splash} = \frac{L}{2} = \frac{3.57}{2} = 1.78\ \text{m}$$
Tóm tắt kết quả thiết kế:
- 5 hàng phần tử gồ, h=0.42 m
- Chiều dài vùng gồ + mở rộng tiết diện: 5×3.57=17.85 m
- Vận tốc tại cửa xả: 2.8 m/s
- Giảm vận tốc: 58%
7.1.2 Dòng Chảy Tumbling Trong Cống Tròn
Dòng chảy tumbling trong các cống tròn có thể đạt được bằng cách chèn các vòng tròn bên trong thân cống như được minh họa trong Hình 7.4. Các yếu tố hình học trở nên phức tạp hơn, nhưng hiện tượng dòng chảy tumbling thì giống như trong các cống hộp. Đối với các cống hộp, chỉ xét đến các phần tử gồ ở đáy, trong khi với các cống tròn, các phần tử là những vòng tròn kín hoàn toàn. Cống được xem như một kênh hở, điều này giúp đơn giản hóa việc thảo luận, và đường kính được điều chỉnh để có đủ khoảng trống phía trên cho dòng chảy mặt tự do.
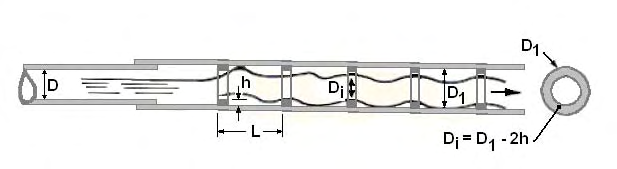
Các quy trình thiết kế đã được mô tả bởi Wiggert và Erfle (1971). Các thí nghiệm của họ về dòng chảy tumbling trong cống tròn được thực hiện với một mô hình plexiglass đường kính 152 mm (6 in) và một cống mẫu bê tông đường kính 457 mm (18 in). Độ dốc dao động từ 0 đến 25 phần trăm, tỷ lệ h/D₁ dao động từ 0.06 đến 0.15 và tỷ lệ L/D₁ dao động từ 0.3 đến 3.0 (L/h từ 5 đến 20). Các biến số thí nghiệm được minh họa trong Hình 7.4. Các biến số xác định việc có xảy ra dòng chảy tumbling hay không bao gồm: chiều cao phần tử gồ, khoảng cách L, độ dốc S₀, lưu lượng Q, và đường kính D₁.
Một mối quan hệ hàm số cho chiều cao phần tử gồ có thể được mô tả như sau:
$$h = f(L, S₀, Q, D₁, g)$$
Thiết lập các nhóm không thứ nguyên cho thấy:
$$h/D₁ = f(L/D₁, S₀, Q/(gD₁^5)^{1/2})$$
Các giới hạn thiết kế thực tiễn có thể được gán cho h/D₁ và L/D₁ để đơn giản hóa mối quan hệ hàm. Dựa trên các quan sát định tính trong phòng thí nghiệm, dòng chảy tumbling dễ được duy trì nhất khi L/D₁ nằm trong khoảng từ 1.5 đến 2.5 và khi h/D₁ nằm trong khoảng từ 0.10 đến 0.15. Gán các giới hạn này cho các cống tròn là tương đương với việc gán các giá trị cho L/h trong quy trình thiết kế cho các cống hộp. Mối quan hệ hàm số trước đó có thể được viết lại thành:
$$\text{Hằng số} = f(S₀, Q/(gD₁^5)^{1/2})$$
hoặc
$$Q/(gD₁^5)^{1/2} = f(S₀)$$
Về mặt lý thuyết, f(S₀) có thể là bất kỳ hàm nào liên quan đến yếu tố độ dốc. Theo kinh nghiệm, f(S₀) được tìm thấy là gần như hằng số. Mức độ phụ thuộc nhẹ của f(S₀) vào độ dốc được coi là ít quan trọng hơn nhiều so với các sai số liên quan đến việc đo đặc tính dòng chảy qua các phần tử gồ lớn. Dựa trên mô hình và dữ liệu mẫu, f(S₀) dao động từ 0.21 đến 0.32 nếu độ dốc nằm trong khoảng từ 4% đến 25%. Với độ dốc nhỏ hơn 4%, cống nên được thiết kế để chảy đầy thay vì dòng chảy tumbling. (Xem Mục 7.2.)
Với giới hạn thực nghiệm của f(S₀), biểu thức sau được phát triển:
$$0.21 < \frac{Q}{\sqrt{g D_1^5}} < 0.32$$
Viết lại để sử dụng trong thiết kế:
$$1.6\left(\frac{Q^2}{g}\right)^{1/5} < D_1 < 1.9\left(\frac{Q^2}{g}\right)^{1/5}\tag{7.10}$$
trong đó:
- \(D_1\) = Đường kính của đoạn cống mở rộng, m (ft)
Phương trình 7.10 là phương trình cơ bản để thiết kế dòng chảy tumbling trong các cống tròn có độ dốc lớn. Nếu đường kính của đoạn cống có gồ được thiết kế theo phương trình này, dòng chảy tumbling sẽ xảy ra và vận tốc đầu ra sẽ gần bằng vận tốc tới hạn. Thiết kế này bị giới hạn bởi các điều kiện sau:
1. \(0L/D_1 \approx 2.0 \) (dung sai ±25%)
2. \(h/D_1 \approx 0.125\) (dung sai ±20%)
3. \(S_0 \) lớn hơn 4% và nhỏ hơn 25%
Vì dòng chảy tumbling là hiện tượng xảy ra trong kênh hở nên lực trọng trường chiếm ưu thế và số Froude, \(V/(gy)^{1/2}\), nên được sử dụng làm cơ sở để thiết kế (hoặc giải thích kết quả mô hình). Watts (1968) đã xác định, dựa trên nhiều tài liệu, rằng h/y là một tham số tỷ lệ quan trọng cho các phần tử gồ trong dòng chảy kênh hở. Trong cả hai biểu thức không thứ nguyên này, y là độ sâu đặc trưng của dòng chảy. Việc sử dụng \(D_1\) thay cho độ sâu đặc trưng trong \(Q/\sqrt{gD_1^5}\) phải được kiểm tra cẩn thận đối với các cống không chảy đầy. Độ sâu đặc trưng cho dòng chảy tumbling, tuy nhiên, là độ sâu tới hạn, được xác định duy nhất bởi Q và D₁; do đó \(D_1\) có thể được thay thế cho y trong trường hợp đặc biệt của cống không chảy đầy.
Ngoài ra, hệ số lớn hơn trong Phương trình 7.10 là từ dữ liệu mô hình 152 mm (6 in) thay vì mẫu thực tế 457 mm (18 in). Sự khác biệt giữa dữ liệu mô hình và mẫu thực tế được quy cho các khó khăn trong thí nghiệm với mẫu thực tế; tuy nhiên, nếu có sai số, chúng có vẻ mang xu hướng an toàn hơn.
Cũng như trong các cống hộp, một mối quan ngại lớn là bùn có thể tích tụ phía trước các phần tử gồ và làm cho chúng mất tác dụng. Điều này có thể không đáng ngại vì các phần tử gồ tăng khả năng vận chuyển trầm tích và có xu hướng tự làm sạch. Trong danh sách ứng dụng ban đầu, Peterson và Mohanty (1960) ghi chú rằng “bằng cách sử dụng phần tử gồ để tạo ra nhiễu động lớn hơn, khả năng vận chuyển trầm tích của kênh có thể được tăng lên.”
Nước bị giữ lại giữa các phần tử có thể gây ra khó khăn trong mùa khô do đóng băng, tan băng và sinh sản côn trùng. Các khe hẹp trong các vòng gồ (nhỏ hơn 0.5h) có thể được sử dụng để thoát nước hoàn toàn mà không làm thay đổi tiêu chí thiết kế. Sarikelle và Simon (1980)
Các nghiên cứu thực địa về các vòng gồ bên trong ống tròn cho thấy rằng các thay đổi để dễ dàng lắp đặt (về bản chất là thêm khe) không làm giảm hiệu quả tiêu tán năng lượng.
Năm vòng gồ ở đầu ra của cống là đủ để tạo ra dòng chảy tumbling. Đường kính tính theo Phương trình 7.10 chỉ áp dụng cho đoạn có gồ và không nhất thiết phải giống với phần còn lại của cống. Hiệp hội Ống Bê tông Hoa Kỳ (ACPA, 1972) đã giới thiệu khái niệm ống lồng, trong đó đoạn chính của cống được thiết kế theo các tham số thông thường (có thể là inlet control) và đoạn có gồ được thiết kế theo Phương trình 7.10. Họ đề xuất việc lồng đoạn ống lớn hơn lên đoạn nhỏ hơn “ít nhất là bằng chiều dài của một mối nối thông thường và sử dụng vật liệu làm kín thông thường trong khe vòng.” Khái niệm này được thể hiện trong Hình 7.4.
Quy trình thiết kế yêu cầu tính toán cả độ sâu normal trong cống dựa trên đường kính cống D và độ sâu tới hạn dựa trên đường kính bên trong của đoạn cống có gồ, Dᵢ. Sử dụng sơ đồ định nghĩa trong Hình 7.5, các mối quan hệ hình học sau được xác định theo độ sâu.
$$\theta = \arccos \left(1 – \frac{2y}{D} \right) \tag{7.11}$$
trong đó:
θ = góc bên trong, đơn vị độ
$$T = D \sin \theta \tag{7.12} $$
$$A = \frac{\theta}{180} \left( \frac{\pi D^2}{4} \right) – \left( \frac{D}{2} \sin \theta \right) \left( \frac{D}{2} – y \right) \tag{7.13}$$
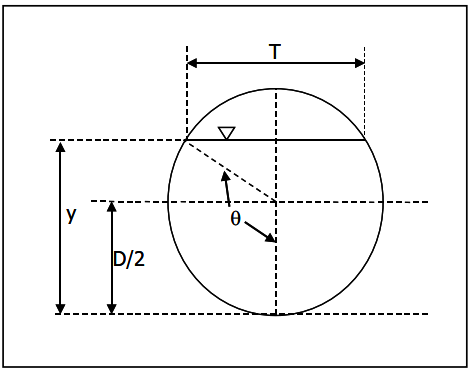
Trong hình minh họa:
- y: độ sâu dòng chảy từ đáy lên đến mặt nước
- D: đường kính ống
- θ: góc nội tại tại tâm hình tròn giới hạn mặt cắt ướt
- T: chiều rộng mặt nước ứng với độ sâu y
Vận tốc tại cửa ra cho dòng chảy tumbling xấp xỉ bằng vận tốc tới hạn. Nó có thể được tính bằng cách xác định độ sâu tới hạn, \(y_c\), cho đường kính trong của các vòng tạo gồ. Dòng chảy tới hạn trong một kênh hở với bất kỳ hình dạng nào sẽ xảy ra khi:
$$\frac{Q^2 T_c}{g A_c^3} = 1 \tag{7.14}$$
trong đó:
- \(T_c\) = bề rộng mặt nước tại điều kiện dòng chảy tới hạn, m (ft)
- \(A_c\) = diện tích dòng chảy tại điều kiện dòng chảy tới hạn, m (ft)
Sau khi xác định được độ sâu tới hạn, vận tốc tới hạn được tính bằng cách sử dụng phương trình liên tục.
Ví dụ thiết kế: Dòng chảy tumbling trong cống tròn (SI)
Thiết kế cống tròn bê tông cho dòng chảy tumbling. Xác định xem vận tốc tại cửa ra có nhỏ hơn 3 m/s hay không.
Cho:
Q = 2.8m3/s
D = 1.2m
n = 0.013
So = 0.06m/m
Giải
Bước 1. Xác minh rằng cống đang trong điều kiện inlet control. Trong ví dụ này, cống đang trong điều kiện inlet control.
Bước 2. Tính toán điều kiện dòng chảy normal. Sử dụng phương pháp thử và sai và các mối quan hệ hình học của các phương trình 7.11, 7.12 và 7.13:
- \(y_n = 0.445 \, m\)
- \(V_n = 7.3 \, m/s \) (Vì lớn hơn 3 m/s nên cần tiêu tán năng lượng.)
Bước 3. Tính toán độ sâu tới hạn và vận tốc tới hạn. Trước tiên cần tính đường kính đoạn cống có bố trí các phần tử gồ sử dụng Phương trình 7.10 và chọn giá trị trung bình của khoảng giới hạn:
$$D_1 = 1.75 \left( \frac{Q^2}{g} \right)^{1/6} = 1.75 \left( \frac{2.8^2}{9.81} \right)^{1/6} = 1.67 \, m$$
$$h = 0.125 D_1 = 0.125(1.67) = 0.21 \, m$$
$$D_i = D_1 – 2h = 1.67 – 2(0.21) = 1.25 \, m$$
Sử dụng phương pháp thử và sai, dùng Phương trình 7.14 và \(D = D_i\):
- \(y_c = 0.913 \, m\)
- \(A_c = 0.961 \, m^2\)
- \(V_c = Q/A_c = 2.8/0.961 = 2.9 \, m/s\) (Thỏa tiêu chuẩn thiết kế 3 m/s)
Bước 4. Xác định thành phần thiết kế còn lại: khoảng cách giữa các phần tử.
$$L = 2D_1 = 2(1.67) = 3.34 \, m$$
Tóm tắt kết quả thiết kế (xem hình minh họa bên dưới; tất cả kích thước nếu không ghi chú khác đều tính bằng mét):
- 5 hàng phần tử, h=0.21 m
- Chiều dài vùng gồ và mở rộng, \(L_m = 16.7 \, m\)
- Vận tốc tại cửa ra = vận tốc tới hạn = 2.9 m/s (giảm vận tốc = 60%)

7.2 Tăng Sức Cản
Phương pháp được mô tả trong mục này liên quan đến việc sử dụng các phần tử gồ để tăng sức cản và làm giảm vận tốc. Việc tăng sức cản có thể khiến cống chuyển từ chế độ chảy không đầy sang chảy đầy trong vùng có gồ. Giảm vận tốc được thực hiện bằng cách tăng diện tích ướt cũng như tăng lực cản và độ rối do các phần tử gồ gây ra.
Dòng chảy tumbling, như đã mô tả trong mục trước, là điều kiện thiết kế giới hạn đối với các phần tử gồ trên các dốc lớn. Dòng chảy tumbling về cơ bản sẽ đưa dòng chảy tại cửa ra về mức vận tốc tới hạn. Nếu yêu cầu là vận tốc tại cửa ra nằm giữa vận tốc tới hạn và vận tốc normal, thì việc thiết kế tăng sức cản trong thân cống là một lựa chọn khả thi.
Tình huống rõ ràng nhất cho việc áp dụng phương pháp tăng sức cản trong thân cống là khi cống chảy không đầy với điều kiện inlet control. Mục tiêu là buộc cống chảy đầy gần đầu ra của cống mà không tạo ra mực nước headwater cao hơn. Mặc dù dựa trên các nguyên lý giống nhau, cách tiếp cận thiết kế cho cống tròn và cống hộp là khác nhau.
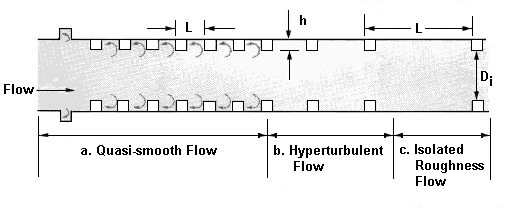
Morris (1963) đã nghiên cứu tất cả các dữ liệu có liên quan đến dòng chảy trong ống gồ và kết luận rằng có ba chế độ dòng chảy, mỗi chế độ có một quan hệ sức cản khác nhau. Về mặt khái niệm, mô tả các chế độ dòng chảy này cũng áp dụng cho cống hộp. Ba chế độ được minh họa trong Hình 7.6 là:
- Dòng chảy gần như trơn (Quasi-smooth flow): Chỉ xảy ra khi có các chỗ lõm hoặc khi các phần tử gồ được bố trí rất gần nhau (L/h xấp xỉ bằng 2). Dòng chảy gần như trơn không quan trọng trong cuộc thảo luận này.
- Dòng chảy siêu rối (Hyper-turbulent flow): Xảy ra khi các phần tử gồ đủ gần nhau sao cho mỗi phần tử nằm trong vùng ảnh hưởng của phần tử trước, và các xoáy bề mặt gồ là nguồn chủ yếu gây ra lực cản ma sát tổng thể.
- Dòng chảy với gồ tách biệt (Isolated roughness flow): Xảy ra khi khoảng cách giữa các phần tử gồ lớn, và lực cản tổng thể là do lực kéo trên bề mặt cống cộng với lực cản hình dạng trên các phần tử gồ.
Quy trình thiết kế để tăng sức cản trong cống hộp và cống tròn có thể được tóm tắt theo các bước sau:
Bước 1. Xác minh rằng cống đang trong điều kiện inlet control.
Bước 2. Tính toán các điều kiện dòng chảy normal trong cống để xác định xem điều kiện xả tại cửa ra có cần giảm thiểu hay không.
Bước 3. Chọn các tỷ lệ kích thước ban đầu. Xác định hệ số nhám Manning’s n cho đoạn cống bố trí gồ.
Bước 4. Tính toán độ sâu và vận tốc sau khi đã giảm thiểu. Kiểm tra vận tốc đã giảm so với tiêu chí thiết kế. Một trong ba điều kiện sau sẽ được quan sát:
- Độ sâu tính được sẽ vượt quá chiều cao của cống, có nghĩa là cống sẽ chảy đầy và có khả năng tăng headwater. Trong các trường hợp như vậy, cần tăng kích thước đoạn gồ và lặp lại bước 3.
- Độ sâu tính được nhỏ hơn chiều cao cống và vận tốc nhỏ hơn tiêu chí thiết kế. Đây là một thiết kế chấp nhận được. Xác minh rằng công suất dòng chảy đầy lớn hơn lưu lượng thiết kế. Nếu không, lặp lại bước 3.
- Độ sâu tính được nhỏ hơn chiều cao cống, nhưng vận tốc lớn hơn tiêu chí thiết kế, thì có thể theo đuổi một trong ba phương án sau: a. Tăng chiều cao của phần tử gồ để đạt gần đến dòng chảy đầy (và do đó làm giảm vận tốc). Lặp lại bước 3. b. Sử dụng thiết kế dòng chảy cuộn (tumbling flow) được trình bày trong Mục 7.1.1. c. Sử dụng loại cấu trúc tiêu năng khác thay thế hoặc kết hợp với phương án tăng gồ.
Bước 5. Hoàn tất việc xác định chiều cao phần tử, khoảng cách phần tử và các đặc điểm thiết kế khác. Chi tiết thiết kế khác nhau cho cống hộp và cống tròn và sẽ được trình bày trong các mục sau.
7.2.1 Tăng sức cản trong cống tròn
Wiggert và Erfle (1971) đã nghiên cứu hiệu quả của các vòng gồ (roughness rings) để tiêu năng trong các cống tròn. Mặc dù nghiên cứu của họ chủ yếu là nghiên cứu về tumbling flow, họ nhận thấy trong nhiều thí nghiệm rằng họ có thể giảm vận tốc hơn 50% mà không cần đạt đến mức độ gồ cần thiết cho tumbling flow. Họ không đưa ra các phương trình tính sức cản, nhưng đã xác lập được các giới hạn thiết kế xấp xỉ.
Từ các nghiên cứu này, hiệu quả tốt được ghi nhận khi tỷ lệ h/D nằm trong khoảng từ 0.06 đến 0.09 với năm vòng. (Xem Hình 7.7.) Việc nhân đôi chiều cao, h₁, của vòng đầu tiên tỏ ra hiệu quả trong việc kích hoạt dòng đầy trong vùng có bề mặt gồ ghề. Hiệu suất phù hợp cũng thu được với bốn vòng giống hệt nhau, nhưng với khoảng cách gấp đôi giữa hai vòng đầu tiên. Tuy nhiên, chiều dài ống không thay đổi nếu giữ khoảng cách đồng đều và sử dụng năm vòng, với vòng đầu tiên có chiều cao gấp đôi bốn vòng còn lại. Vòng bổ sung này sẽ giúp thiết lập điều kiện dòng đầy như giả định. Ngoài ra, vòng cuối cùng (hạ lưu) phải được đặt cách đầu ra của cống không nhỏ hơn một nửa khoảng cách giữa các vòng.
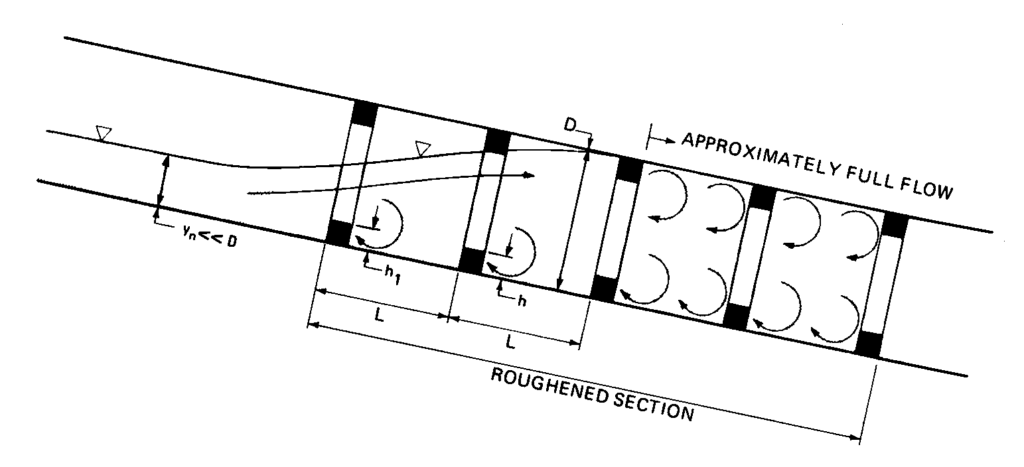
Kinh nghiệm sau đó được báo cáo bởi Hiệp hội Ống Bê tông Hoa Kỳ (ACPA, 1972) cho thấy cần xem xét các giá trị nhỏ hơn của h/D, và thiết lập các đường cong sức cản xấp xỉ để đánh giá thiết kế nhằm tránh các lắp đặt dẫn đến dòng chảy đầy lan truyền ngược về phía cửa vào cống.
Dựa trên kinh nghiệm với các phần tử lớn được sử dụng để tạo tumbling flow (xem Mục 7.1) và công trình của Wiggert và Erfle (1971), năm hàng phần tử gồ ghề với chiều cao dao động từ 5 đến 10 phần trăm đường kính cống là đủ.
Một yếu tố then chốt trong thiết kế các phần tử gồ tăng cường là xác định chế độ dòng chảy gồ ghề và tiếp theo là giá trị Manning’s n thích hợp. Mặc dù phần lớn tài liệu liên quan đến các phần tử gồ lớn trong ống tròn biểu thị sức cản dưới dạng hệ số ma sát f, tất cả các phương trình sức cản đều được chuyển đổi thành biểu thức n của Manning trong tài liệu hướng dẫn này.
7.2.1.1 Isolated-Roughness Flow (Dòng chảy gồ tách biệt)
Dòng chảy gồ tách biệt đã được giới thiệu trong Mục 7.2. Tổng lực ma sát hoặc lực cản, \(f_{IR}\), bao gồm hai phần:
$$f_{IR} = f_s + f_d \tag{7.15}$$
trong đó:
- \(f_s\) = lực ma sát trên bề mặt cống.
- \(f_d\) = lực ma sát do lực cản hình thể từ các phần tử gồ.
Lực ma sát do lực cản hình thể phụ thuộc vào hệ số cản của hình dạng phần tử, tỷ lệ phần trăm chu vi ướt có phần tử gồ, kích thước và khoảng cách giữa các phần tử gồ, và vận tốc dòng chảy tác động lên chúng. Morris (1963) đã liên hệ vận tốc với lực cản bề mặt và đưa ra phương trình sau:
$$f_{IR} = f_s \left( 1 + 67.2C_D \left( \frac{L_r}{P} \right) \left( \frac{h}{r_i} \right) \left( \frac{r_i}{L} \right) \right) \tag{7.16}$$
trong đó:
- \(C_D\) = hệ số cản theo hình dạng phần tử gồ ghề.
- \(L_r / P\) = tỷ lệ tổng chiều dài chu vi của các phần tử gồ ghề trên tổng chu vi ướt.
- \(r_i\) = bán kính ống, được xác định từ đường kính trong của các vòng gồ ghề, đo từ đỉnh đến đỉnh.
Lưu ý: \(L_r\) có thể nhỏ hơn P để dễ chế tạo hoặc cho phép dòng nhỏ chảy qua phần đáy vòng.
Trong các nghiên cứu của Morris, ông sử dụng kích thước từ đỉnh đến đỉnh của vòng gồ như là đường kính hiệu dụng \(D_i\). Để chuyển biểu thức lực cản sang dạng hệ số Manning’s n, cần các biểu thức sau:
$$f_s = \alpha \left( \frac{n}{D^{1/6}} \right)^2$$
$$f_{IR} = \alpha \left( \frac{n_{IR}}{D_i^{1/6}} \right)^2$$
α là hằng số chuyển đổi đơn vị, bằng 124 trong hệ SI và 184 trong hệ CU. Phương trình 7.16 sau đó có thể được chuyển đổi sang hệ số Manning’s n:
$$n_{IR} = n \left( \frac{D_i}{D} \right)^{1/6} \left( 1 + 67.2 C_D \left( \frac{L_r}{P} \right) \left( \frac{h}{L} \right) \right)^{1/2} \tag{7.17}$$
trong đó:
- \(n_{IR}\) = hệ số Manning tổng thể cho dòng chảy gồ tách biệt
- n = hệ số Manning của bề mặt cống không có vòng gồ
- D = đường kính danh định của cống (m hoặc ft)
- \(D_i\) = đường kính trong của vòng gồ (m hoặc ft), với \(D_i = D – 2h\)
Lưu ý:
Đối với phần tử gồ hình chữ nhật có cạnh sắc, giá trị hằng số 1.9 có thể được sử dụng cho \(C_D\).
Đáng chú ý là lực cản tổng thể \(n_{IR}\) giảm khi tỷ số khoảng cách tương đối \(L/D_i\) tăng trong chế độ dòng chảy này.
7.2.1.2 Dòng chảy siêu rối (Hyperturbulent Flow)
Lực ma sát trong chế độ này độc lập với ma sát trên bề mặt cống:
$$f_{HT} = \left( \frac{1}{2 \log \left( \frac{r_i}{L} \right) + 1.75 + \phi} \right)^2 \tag{7.18}$$
trong đó,
\(f_{HT}\) = lực cản tổng thể đối với dòng chảy siêu rối
ϕ = hàm số của số Reynolds, hình dạng phần tử, và khoảng cách tương đối
Bằng cách giới hạn việc áp dụng phương trình 7.18 đối với các vòng gồ có cạnh sắc và với khoảng cách lớn hơn bán kính ống, ϕ có thể được bỏ qua.
Thay thế biểu thức sau: \(f_{HT} = \alpha \left( \frac{n_{HT}}{D_i^{1/6}} \right)^2\)
Phương trình 7.18 sau đó có thể chuyển sang hệ số Manning’s n:
$$n_{HT} = \frac{\alpha D_i^{1/6}}{2 \log \left( \frac{r_i}{L} \right) + 1.75} \tag{7.19}$$
trong đó,
\(n_{HT}\) = hệ số Manning đối với dòng chảy siêu rối
α = hằng số chuyển đổi đơn vị, 0.0898 (SI) và 0.0737 (CU)
Chiều cao của phần tử gồ, h, đã được tích hợp sẵn trong \(D_i\).
Từ phương trình 7.19 có thể thấy rằng \(n_{HT}\) tăng khi khoảng cách tăng đối với chế độ dòng chảy này.
7.2.1.3 Ranh giới chế độ dòng chảy (Regime Boundaries)
Vì lực cản tăng lên khi khoảng cách tăng đối với chế độ dòng chảy siêu rối (hyper-turbulent), và khi khoảng cách giảm đối với chế độ dòng chảy với gồ tách biệt (isolated roughness), nên ranh giới giữa hai chế độ xảy ra khi các phương trình lực cản bằng nhau. Ranh giới này được xác định bằng cách cho \(n_{IR}\) trong Phương trình 7.17 bằng với \(n_{HT}\) trong Phương trình 7.19. Trong thiết kế, cả hai đều được tính; giá trị n nhỏ hơn sẽ được sử dụng và chỉ ra chế độ dòng chảy nào được áp dụng.
Thiết kế được khuyến nghị giới hạn trong các điều kiện sau:
- \(0.5 < L/D_i < 1.5\) (1.0 đến 1.1 là điểm bắt đầu khuyến nghị)
- \(0.05 < h/D_i < 0.10\) (0.06 là điểm bắt đầu khuyến nghị với các vòng gồ có cạnh sắc)
Khi các khoảng giới hạn này đã được chọn, chiều cao phần tử gồ được tính như sau:
$$h = \frac{D}{2 + \frac{1}{c}} \tag{7.20}$$
trong đó,
h = chiều cao phần tử gồ, m (ft)
c = tỷ lệ của \(h/D_i\)
Khi đã tính được h, các giá trị của \(D_i\) và L sẽ được suy ra trực tiếp và các giá trị gồ sẽ được tính toán.
Ví dụ thiết kế: Tăng sức cản trong cống tròn (SI)
Thiết kế một cống bê tông tròn để tăng độ nhám. Xác định xem vận tốc tại cửa ra có nhỏ hơn 3 m/s hay không.
Cho:
- Q=2.8 m3/s
- D=1.2 m
- n=0.013
- So=0.06 m/m
Giải:
Bước 1. Xác minh rằng cống ở trong điều kiện inlet control. Trong trường hợp này, cống nằm trong inlet control.
Bước 2. Tính toán điều kiện dòng chảy normal. Sử dụng phương pháp thử – sai và các mối quan hệ hình học từ các phương trình 7.11, 7.12 và 7.13:
- \(y_n = 0.445 \, \text{m}\)
- \(V_n = 7.3 \, \text{m/s}\)
(Vì lớn hơn 3 m/s nên cần tiêu năng.)
Bước 3. Chọn tỷ lệ thiết kế ban đầu và xác định hệ số Manning’s n cho phần ống làm gồ.
Giả sử:
- \(L/D_i = 1.1\) và \(h/D_i = 0.06\)
Tính h theo Phương trình 7.20:
$$h = \frac{D}{2 + \frac{1}{c}} = \frac{1.2}{2 + \frac{1}{0.06}} = 0.064 \, \text{m} \rightarrow làm tròn: 0.06 \, \text{m}$$
- \(D_i = D – 2h = 1.2 – 2(0.06) = 1.08 \, \text{m}\)
- \(L = 1.1D_i = 1.1(1.08) = 1.19 \, \text{m}\)
Với thiết kế này, không có khoảng trống giữa các vòng, nên \(L_r/P = 1\)
Tính hệ số Manning n cho hai trường hợp:
1. Gồ tách biệt (isolated roughness) phương trình 7.17:
$$n_{IR} = n \left(\frac{D_i}{D}\right)^{1/6} \left[1 + 67.2 C_D \left(\frac{L_r}{P}\right)\left(\frac{h}{L}\right)\right]^{1/2} = 0.013 \left(\frac{1.08}{1.2}\right)^{1/6} \left[1 + 67.2(1.9)\left(1\right)\left(\frac{0.060}{1.19}\right)\right]^{1/2} = \mathbf{0.035}$$
2. Dòng siêu rối (hyperturbulent) phương trình 7.19:
$$n_{HT} = \frac{\alpha D_i^{1/6}}{2\log\left(\frac{r_i}{L}\right) + 1.75} = \frac{0.0898(1.08)^{1/6}}{2\log\left(\frac{0.54}{1.19}\right) + 1.75} = \mathbf{0.085}$$
Kết luận:
Vì \(n_{IR} < n_{HT}\) → loại dòng chảy là isolated roughness
Chọn \(n = \mathbf{0.035}\)
Bước 4. Tính độ sâu và vận tốc sau khi giảm tốc. Kiểm tra vận tốc này với tiêu chí thiết kế.
Với đường kính trong \(D_i\), và giá trị hệ số Manning n tính được ở bước 3, độ sâu normal trong điều kiện đã làm nhám được xác định (bằng phương pháp thử – sai) như sau:
- \(y_n = 0.932 \, \text{m}\)
- \(V_n = 3.3 \, \text{m/s}\)
So sánh với mục tiêu thiết kế là 3.0 m/s, vận tốc này là không chấp nhận được dù đã được giảm đáng kể so với vận tốc ban đầu chưa giảm. Vì độ sâu nhỏ hơn \(D_i,\) ta có thể tăng h để làm giảm vận tốc thêm nữa.
(Lưu ý: Cần tăng đường kính cống vì vận tốc dòng chảy đầy vẫn là 3.1 m/s, vượt tiêu chí thiết kế).
→ Cần lặp lại Bước 3 và 4.
Bước 3 (lặp lần 2): Chọn tỷ lệ thiết kế thử và xác định hệ số Manning n cho phần ống được bố trí gồ.
- Giữ nguyên \(L/D_i = 1.1\)
- Tăng đường kính D = 1.50 m (kích thước lớn nhất tiếp theo)
- Chọn h=0.1 m
Tính:
- \(D_i = D – 2h = 1.50 – 2(0.10) = 1.30 \, \text{m} \Rightarrow h/D_i = 0.077\)
- \(L = 1.1 D_i = 1.1(1.3) = 1.43 \, \text{m}\)
Với thiết kế này, sẽ không có khe hở giữa các vòng nhám, do đó:
- \(L_r/P = 1\)
Tiếp theo, sẽ tính hệ số Manning n cho hai loại dòng:
- Isolated roughness → dùng phương trình 7.17
- Hyperturbulent flow → dùng phương trình 7.19
Việc so sánh hai giá trị sẽ xác định được chế độ dòng chảy và giá trị n cần dùng.
$$n_{IR} = n \left( \frac{D_i}{D} \right)^{1/6} \left( 1 + 67.2 C_D \left( \frac{L_r}{P} \right) \left( \frac{h}{L} \right) \right)^{1/2} = 0.013 \left( \frac{1.30}{1.50} \right)^{1/6} \left( 1 + 67.2(1.9)(1)\left( \frac{0.10}{1.43} \right) \right)^{1/2} = 0.040$$
$$n_{HT} = \frac{\alpha D_i^{1/6}}{2 \log \left( \frac{r_i}{L} \right) + 1.75} = \frac{0.0898(1.30)^{1/6}}{2 \log \left( \frac{0.65}{1.43} \right) + 1.75} = 0.088$$
Vì \(n_{IR} < n_{HT}\), nên độ gồ được phân loại là isolated roughness và n = 0.040.
Bước 4 (lần lặp thứ hai). Tính thử chiều sâu và vận tốc đã giảm nhẹ. Kiểm tra vận tốc đã giảm so với tiêu chí thiết kế.
Với đường kính trong \(D_i\), và các giá trị Manning’s n đã tính trong bước 3, chiều sâu dòng chảy normal cho điều kiện đã làm gồ được tính bằng phương pháp thử và sai như sau:
- \(y_n = 1.025 \, \text{m}\)
- \(V_n = 2.5 \, \text{m/s}\)
So với mục tiêu thiết kế là 3.0 m/s, vận tốc này là chấp nhận được. Tuy nhiên, ta cần kiểm tra công suất xả của cống bằng cách sử dụng phương trình Manning.
Giả sử cống chảy đầy và ước tính chu vi ướt như sau:
- \(A = \pi D_i^2 / 4 = \pi (1.30)^2 / 4 = 1.33 \, \text{m}^2\)
- \(P = \pi D_i = \pi (1.30) = 4.08 \, \text{m}\)
- \(R = A / P = 1.33 / 4.08 = 0.326 \, \text{m}\)
Áp dụng phương trình Manning:
$$Q = \frac{1}{n} AR^{2/3} S^{1/2} = \frac{1}{0.040} 1.33(0.326)^{2/3}(0.06)^{1/2} = 3.9 \, \text{m}^3/s\)
Vì lưu lượng này lớn hơn lưu lượng thiết kế là 2.8 m³/s nên thiết kế này là chấp nhận được. Nếu không đạt, cần xem xét cống lớn hơn hoặc quay lại bước 3, hoặc thiết kế dòng tumbling flow hay các loại tiêu năng khác.
Bước 5. Hoàn tất việc tính chiều cao phần tử gồ, khoảng cách các phần tử và các đặc điểm thiết kế khác.
Chiều cao và khoảng cách phần tử gồ đã được xác định, cũng như kích thước cống mở rộng. Với 5 hàng phần tử gồ, chiều dài của đoạn mở rộng có gồ là 5.06 m.
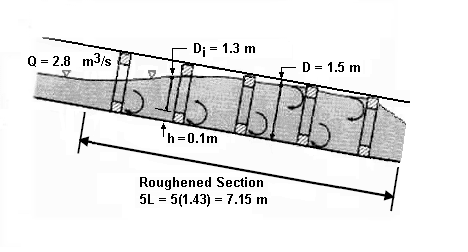
Tóm tắt kết quả thiết kế (xem hình minh họa bên dưới):
- 5 hàng phần tử gồ, h=0.1 m
- Chiều dài đoạn bố trí gồ = 7.15 m. (Chiều dài làm nhám được tính từ L/2 trước phần tử đầu tiên và phần tử nhám cuối cách miệng cống ít nhất L/2)
- Vận tốc đầu ra = 2.9 m/s. (Giảm vận tốc = 60%)
7.2.2 Tăng sức cản trong cống hộp
Tài liệu cho phần này chủ yếu được lấy từ một báo cáo sơ bộ của FHWA về các vách ngăn cá trong cống hộp (Normann, 1974). Báo cáo này sử dụng phân loại các chế độ dòng chảy và phương trình ma sát cơ bản của Morris (Morris, 1963), nhưng với một vận tốc đại diện phù hợp hơn, \(V_A\), trong một trong các chế độ đó. Dữ liệu thực nghiệm của Shoemaker (1956) cũng được sử dụng để xác định các đường cong chuyển tiếp. Vì nhiều lý do, các sửa đổi đối với thiết kế vách ngăn cá là cần thiết để thích nghi với thiết kế cấu trúc tiêu năng. Trong thiết kế vách ngăn cá, mối quan tâm là có được một ước lượng an toàn của sức cản để tính toán kích thước cống; trong khi đó, trong tài liệu này, ước lượng an toàn của vận tốc đầu ra cũng rất quan trọng. Ngoài ra, các đường cong thiết kế vách ngăn cá chỉ liên quan đến độ gồ ở đáy.
Như trước đó, cả hai chế độ dòng siêu rối và gồ tách biệt (hyperturbulent and isolated roughness) đều được xem xét. Đối với cống hộp trong dòng siêu rối, hệ số độ nhám Manning có thể được ước tính bằng:
$$n_{HT} = n \left[ \left( 1 – \frac{L_r}{P} \right) + \frac{70.6 \left( \frac{L_r}{P} \right)}{\left( 2 \log \left( \left( \frac{R_i}{h} \right) \left( \frac{h}{L} \right) \right) + 1.75 \right)^2} \right]^{1/2}\tag{7.21}$$
trong đó:
- \(n_{HT}\) = hệ số độ nhám Manning cho chế độ dòng siêu rối
- n = hệ số độ nhám Manning cho cống không có các phần tử tạo gồ
(giá trị tối đa của n là 0.015 cho phương trình này) - \(L_r / P\) = tỷ số giữa tổng chiều dài tiếp xúc của các phần tử gồ và chu vi ướt tổng cộng
Đối với chế độ dòng chảy isolated roughness, phạm vi cao và thấp của hệ số Manning được xem xét như được thể hiện qua các phương trình sau:
$$n_{IR,LOW} = n \left[1 + 200 \left( \frac{h}{L} \right) \left( \frac{L_r}{P} \right) \right]^{1/2} \tag{7.22a}$$
$$n_{IR,HIGH} = n \left[1 + 390 \left( \frac{h}{L} \right) \left( \frac{L_r}{P} \right) \right]^{1/2} \tag{7.22b}$$
trong đó:
- \(n_{IR,LOW}\) = hệ số Manning cho chế độ dòng chảy isolated roughness, phạm vi thiết kế thấp để ước lượng vận tốc.
- \(n_{IR,HIGH}\) = hệ số Manning cho chế độ dòng chảy isolated roughness, phạm vi thiết kế cao để ước lượng độ sâu dòng chảy.
- n = hệ số độ nhám Manning cho cống không có các phần tử tạo nhám
(giá trị tối đa của n là 0.015 cho các phương trình này)
\(L_r\) sẽ bằng chiều rộng đáy B, đối với các thiết bị chỉ có gồ đáy, và sẽ bằng chu vi ướt P, khi các phần tử tạo gồ được gắn vào tất cả các mặt hoặc khi các phần tử tạo gồ kéo dài trong toàn bộ dòng chảy. Sự có mặt của các khe thoát nước trong phần tử gồ sẽ bị bỏ qua khi ước lượng \(L_r\).
Các phương trình được xây dựng dựa trên \(C_D = 1.9\), f = 0.14 (trong đó f là hệ số ma sát Darcy cho bề mặt cống không có phần tử gồ), và tỉ số \(V_A / V\) = 0.60 hoặc 0.85. Giá trị thấp hơn của \(V_A / V\) được ngầm bao gồm trong Phương trình 7.22a và giá trị cao hơn được dùng trong Phương trình 7.22b. Việc sử dụng vận tốc tiếp cận đại diện \(V_A\) cho phép đưa vào các thông số của cống mà sẽ có xu hướng hoặc ước lượng quá cao hoặc quá thấp về sức cản. Giả định rằng \((R / R_i)^{1/3}\) xấp xỉ bằng 1 nhằm đơn giản hóa phép tính. R là bán kính thủy lực thực của cống, còn \(R_i\) là bán kính thủy lực tính bên trong các đỉnh của phần tử gồ. Với các thiết kế được xem xét trong phần này, giả định đó là hợp lý.
Trong tài liệu này, việc phát triển cả đường cong sức cản cao và thấp là phù hợp. Thay vì cố gắng xác định chuyển tiếp giữa các đường cong này, một chuyển tiếp đột ngột được sử dụng như là điều kiện xấu nhất cho đường cong cao, và chuyển tiếp theo đường thẳng được xem là điều kiện nhẹ nhất cho các đường cong thấp. Điều này được minh họa trong Hình 7.8. Quan sát của Powell (1946) là cơ sở để giả định phạm vi từ 6 đến 12 của tỷ lệ L/h cho đường cong chuyển tiếp giữa dòng chảy isolated roughness và dòng hyperturbulent. Một giá trị L/h = 10 được chọn cho thiết kế vì nó cho giá trị n lớn nhất.
Để ước lượng vận tốc, phù hợp khi ước lượng sức cản dựa trên mối quan hệ đường thẳng (thấp) được chỉ ra trong Hình 7.8. Do đó, Phương trình 7.21 (dòng hyperturbulent) được tính với L/h = 6 và Phương trình 7.22a (isolated roughness) được tính với L/h = 12. Việc nội suy tuyến tính giữa hai giá trị này khi L/h = 10 dẫn đến mối quan hệ được cung cấp như sau:
$$n_{\text{LOW}} = n \left\{ \frac{2}{3} \left( 1 + 16.7 \left( \frac{L_r}{P} \right) \right)^{1/2} + \frac{1}{3} \left( \left( 1 – \frac{L_r}{P} \right) + \frac{70.6 \left( \frac{L_r}{P} \right)} {\left( 2 \log \left( \frac{R_i}{h} \right) + 0.194 \right)^2} \right)^{1/2} \right\}\tag{7.23}$$
trong đó:
- \(n_{LOW}\): hệ số độ nhám Manning cho trường hợp đường cong sức cản thấp
- n: hệ số độ nhám Manning của cống không có phần tử gồ
- \(L_r / P\): tỷ lệ chiều dài chu vi phần tử gồ so với chu vi ướt
- \(R_i\): bán kính thủy lực tính trong phần tử gồ
- h: chiều sâu dòng chảy
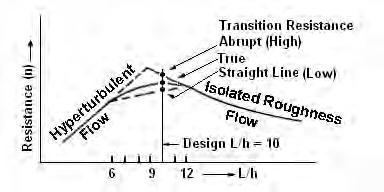
Để xác định giá trị thấp hơn của hệ số Manning, \(n_{LOW}\), nhằm mục đích ước lượng vận tốc đầu ra, Phương trình 7.23 áp dụng cho các giá trị của \(h/R_i\) nhỏ hơn hoặc bằng 0.3. Đối với các tỷ số lớn hơn 0.3, \(n_{LOW}\) được tính trực tiếp từ Phương trình 7.22a với L/h = 10.
Để xác định giá trị cao hơn của hệ số Manning, \(n_{HIGH}\), nhằm mục đích ước lượng độ sâu dòng chảy, giá trị đột ngột (cao) được biểu diễn trong Hình 7.8 là mong muốn. Đối với \(h/R_i\) lớn hơn 0.2, Phương trình 7.22b được đánh giá tại L/h = 10 và sử dụng cho \(n_{HIGH}\). Đối với các tỷ số nhỏ hơn hoặc bằng 0.2, cả Phương trình 7.22b và 7.21 đều được đánh giá tại L/h = 10 và giá trị thấp hơn được chọn làm \(n_{HIGH}\). Cả hai đều được so sánh để tránh các giá trị phi thực tế từ Phương trình 7.22b.
Vì các phương trình trên là các phương trình dòng chảy chuẩn và các phần tử gồ có thể tương đối nhỏ khi sử dụng phương pháp này, cần thiết phải tính chiều dài đoạn cống cần tạo gồ. Phương trình động lượng, được viết cho đoạn cống có bố trí gồ, được sử dụng để tính số hàng phần tử tạo gồ cần thiết.
$$N = \frac{gB(y_n^2 – y_i^2) + 2Q(V_n – V_i)}{C_D A_f V_w^2} \tag{7.24}$$
trong đó:
- N = số hàng phần tử tạo nhám
- B = chiều rộng đáy cống, mét (ft)
- \(y_n\) = chiều sâu chuẩn trong cống trước đoạn có gồ, mét (ft)
- \(y_i\) = chiều sâu chuẩn trong đoạn có gồ của cống, mét (ft)
- \(V_n\) = vận tốc chuẩn trong cống trước đoạn có gồ, m/s (ft/s)
- \(V_i\) = vận tốc chuẩn trong đoạn có gồ của cống, m/s (ft/s)
- \(C_D\) = hệ số cản (lấy là 1.9)
- \(A_f\) = diện tích mặt ướt phía trước của một hàng phần tử gồ, m² (ft²), bằng B(h) đối với gồ đáy
- \(V_w\) = vận tốc trung bình tại tường tác dụng lên các phần tử gồ, m/s (ft/s), bằng \((V_n + V_i)/6\)
Bất kể kết quả từ Phương trình 7.24 ra sao, số hàng phần tử gồ không bao giờ được ít hơn năm.
Ngoài ra, khuyến nghị nên sử dụng một phần tử lớn đặt ở đầu vùng tạo gồ để đẩy nhanh quá trình tiệm cận về dòng chảy normal. Chiều cao đề xuất của phần tử lớn này bằng hai lần chiều cao của các phần tử thông thường. Khoảng cách bố trí giữa các phần tử giống nhau cho tất cả các hàng.
Các khe thoát nước trong phần tử gồ được bố trí để thoát dòng chảy thấp. Khe mở này không được vượt quá h/2.
Quy trình này chỉ áp dụng cho các phần tử gồ dạng thanh đặc với cạnh đầu sắc. Phần tử có mặt cắt ngang hình chữ nhật là phù hợp nhất với các giả định đã đưa ra.
Do đã giả định về phân bố vận tốc, việc áp dụng quy trình này phải giới hạn đối với chiều cao phần tử gồ nhỏ và độ dốc tương đối thoải. Chiều cao phần tử gồ không được vượt quá 10% chiều sâu dòng chảy. Hạn chế này vốn đã được bao hàm trong khoảng giá trị đề xuất của \(h/R_i\) trong quy trình thiết kế.
Thiết kế khuyến nghị giới hạn trong các điều kiện sau:
- \(S_o \leq 6\%\)
- \(0.1 < h/R_i < 0.4\)
- \(L/h = 10\)
Ví dụ thiết kế: Tăng sức cản cho cống hộp (SI)
Thiết kế một cống hộp bê tông với sức cản tăng cường bằng cách sử dụng các phần tử gồ ở đáy. Xác định xem vận tốc tại cửa ra có nhỏ hơn 3 m/s hay không.
Cho:
- Q=2.8 m3/s
- D=1.2 m
- B=1.2 m
- n=0.013
- \(S_o = 0.06 \, \text{m/m}\)
Giải:
Bước 1. Xác minh cống làm việc trong điều kiện inlet control. Trong trường hợp này, cống ở chế độ inlet control.
Bước 2. Tính điều kiện dòng chảy normal. Sử dụng phương pháp thử và sai:
- \(y_n = 0.34 \, \text{m}\)
- \(V_n = 6.8 \, \text{m/s}\) (Vì giá trị này lớn hơn 3 m/s nên cần tiêu tán năng lượng).
Bước 3. Chọn tỉ lệ thiết kế ban đầu. Xác định giá trị hệ số Manning n cho đoạn cống có phần tử gồ nhằm ước lượng độ sâu và vận tốc đã được giảm thiểu.
- Thử L/h=10 và \(h/R_i = 0.3\)
Giả định rằng cống không chảy đầy để tính chu vi ướt.
(Nếu giả sử cống chảy đầy trong phép tính này, nó sẽ bị vượt tải khi tính hệ số Manning cao cho kiểm tra công suất. Việc sử dụng các mặt bên và đáy của cống sẽ cho giá trị nhỏ nhất của chu vi ướt (dưới mức chảy đầy), và do đó, cung cấp giá trị an toàn của n để ước lượng vận tốc trong đoạn có gồ. Giả định này có thể được điều chỉnh trong các bước lặp sau.
- P = 2D + B = 2(1.2) + 1.2 = 3.6m
- \(L_r = B = 1.2 \, \text{m} \) (chỉ có gồ đáy)
Sử dụng Phương trình 7.23 và n=0.013 (giá trị tối đa là 0.015):
$$n_{\text{LOW}} = n \left\{ \frac{2}{3} \left( 1 + 16.7 \left( \frac{L_r}{P} \right) \right)^{1/2} + \frac{1}{3} \left[ \left( 1 – \frac{L_r}{P} \right) + \frac{70.6 \left( \frac{L_r}{P} \right)} {\left( 2 \log \left( \frac{R_i}{h} \right) + 0.194 \right)^2} \right]^{1/2} \right\} = 0.040$$
Bước 4.
Tính độ sâu, vận tốc và chiều cao phần tử gồ đã được giảm thiểu. Kiểm tra vận tốc đã giảm so với tiêu chí thiết kế. Sử dụng phương pháp thử và sai:
- \(y_i = 0.783 \, \text{m}\) (lưu ý rằng cống không chảy đầy)
- \(A_i = 0.783 \cdot 1.2 = 0.940 \, \text{m}^2\)
- \(P_i = 2(0.783) + 1.2 = 2.77 \, \text{m}\)
- \(R_i = \frac{0.940}{2.77} = 0.340 \, \text{m}\)
- \(h = (h / R_i)(R_i) = 0.3(0.340) = 0.102 \, \text{m} \) (làm tròn thành 0.10 m)
- \(V_i = 2.98 \, \text{m/s}\)
Vì vận tốc này nhỏ hơn hoặc bằng 3 m/s, nên thiết kế tiêu năng là đạt yêu cầu. Tuy nhiên, ta phải kiểm tra khả năng thông qua của cống bằng cách sử dụng giá trị ước lượng cao của hệ số Manning từ Phương trình 7.22b. Có hai trường hợp giới hạn dòng chảy có thể xảy ra.
Trường hợp 1: Giả sử cống chảy gần đầy.
Sử dụng Phương trình 7.22b và n=0.013 (giá trị tối đa là 0.015):
$$n_{IR,HIGH} = n \left[ 1 + 390 \left( \frac{h}{L} \right) \left( \frac{L_r}{P} \right) \right]^{1/2} = 0.013 \left[ 1 + 390 (0.1) \left( \frac{1.2}{3.6} \right) \right]^{1/2} = 0.049$$
Diện tích và bán kính thủy lực được tính như sau:
- \(y = D – h = 1.2 – 0.10 = 1.10 \, \text{m}\)
- \(A = yB = 1.10(1.2) = 1.32 \, \text{m}^2\)
- \(P = 2y + B = 2(1.10) + 1.2 = 3.40 \, \text{m}\)
- \(R = A / P = 1.32 / 3.40 = 0.388 \, \text{m}\)
Sử dụng phương trình Manning:
$$Q = \frac{1}{n} AR^{2/3} S^{1/2} = \frac{1}{0.049} \cdot 1.32 (0.388)^{2/3} (0.06)^{1/2} = 3.5 \, \text{m}^3/\text{s}$$
Q lớn hơn lưu lượng thiết kế → cống đạt yêu cầu trong trường hợp này.
Trường hợp 2, giả sử cống chảy đầy. Sử dụng Phương trình 7.22b và n=0.013
(giá trị tối đa là 0.015):
$$n_{IR,HIGH} = n \left[ 1 + 390 \left( \frac{h}{L} \right) \left( \frac{L_r}{P} \right) \right]^{1/2} = 0.013 \left[ 1 + 390(0.1)\left( \frac{1.2}{4.8} \right) \right]^{1/2} = 0.043$$
Diện tích và bán kính thủy lực được tính như sau:
- \(A = yB = 1.10(1.2) = 1.32 \, \text{m}^2\)
- \(P = 2(y + B) = 2(1.10 + 1.2) = 4.6 \, \text{m}\)
- \(R = A / P = 1.32 / 4.6 = 0.287 \, \text{m}\)
Sử dụng phương trình Manning:
$$Q = \frac{1}{n} AR^{2/3} S^{1/2} = \frac{1}{0.043} \cdot 1.32 (0.287)^{2/3} (0.06)^{1/2} = 3.3 \, \text{m}^3/\text{s}$$
Vì cả hai giá trị lưu lượng đều lớn hơn lưu lượng thiết kế là 2.8 m³/s nên ta biết rằng thiết kế là đạt yêu cầu. Nếu không đạt, có thể xem xét sử dụng một ống cống lớn hơn bằng cách quay lại bước 3, hoặc áp dụng dòng chảy tumbling hay một loại cấu trúc tiêu năng khác.
Bước 5.
Hoàn tất việc xác định chiều cao phần tử, khoảng cách giữa các phần tử và các chi tiết thiết kế khác.
Khoảng cách giữa các phần tử tạo nhám được tính như sau:
$$L = \left( \frac{L}{h} \right) h = (10)(0.10) = 1.0 \, \text{m}$$
Số hàng phần tử tạo nhám được ước lượng bằng Phương trình 7.24. Trước hết, tính:
- \(A_f = B(h) = 1.2(0.10) = 0.12 \, \text{m}^2\)
- \(V_w = \frac{V_n + V_i}{6} = \frac{6.8 + 2.98}{6} = 1.63 \, \text{m/s}\)
$$N = \frac{gB(y_n^2 – y_i^2) + 2Q(V_n – V_i)}{C_D A_f V_w^2} = \frac{9.81(1.2)(0.34^2 – 0.783^2) + 2(2.80)(6.8 – 2.98)}{1.9(0.12)(1.63^2)} = 25.7$$
Làm tròn lên số nguyên gần nhất:
N=26
Tóm tắt kết quả thiết kế:
- 26 hàng phần tử gồ, h=0.10 m
- Chiều dài vùng có phần tử gồ = 25.0 m. Phần tử gồ cuối cùng phải cách cửa xả của cống ít nhất là L/2.
- Vận tốc tại cửa ra = 2.98 m/s. (Giảm vận tốc: 57%)
7.3 USBR Type IX Baffled Apron
Peterka (1978) đã mô tả quy trình thiết kế một “baffled apron” (dốc có gồ) sử dụng các phần tử gồ trên sàn của cống hộp hoặc máng như minh họa trong Hình 7.9. Các phần tử gồ, gọi là các vách ngăn hoặc khối, làm nhiễu dòng chảy sao cho dòng chảy sẽ chậm lại khi tiếp cận mỗi khối, sau đó gia tốc khi đi qua khối và tiếp cận hàng tiếp theo.
Bằng cách đặt các vách ngăn từ đỉnh đến đáy của cống hoặc máng, các vách ngăn ngăn không cho dòng chảy gia tốc quá mức, bất kể độ cao rơi tổng thể là bao nhiêu. Dựa trên các nghiên cứu mô hình do Peterka báo cáo, thiết kế baffled apron cho phép vận tốc tại đáy của apron không vượt quá một phần ba vận tốc tới hạn nếu tuân thủ theo hướng dẫn thiết kế.
Phương pháp này hoạt động hiệu quả cả khi có hoặc không có tailwater và nhìn chung không dễ bị tắc nghẽn bởi rác hoặc mảnh vụn.
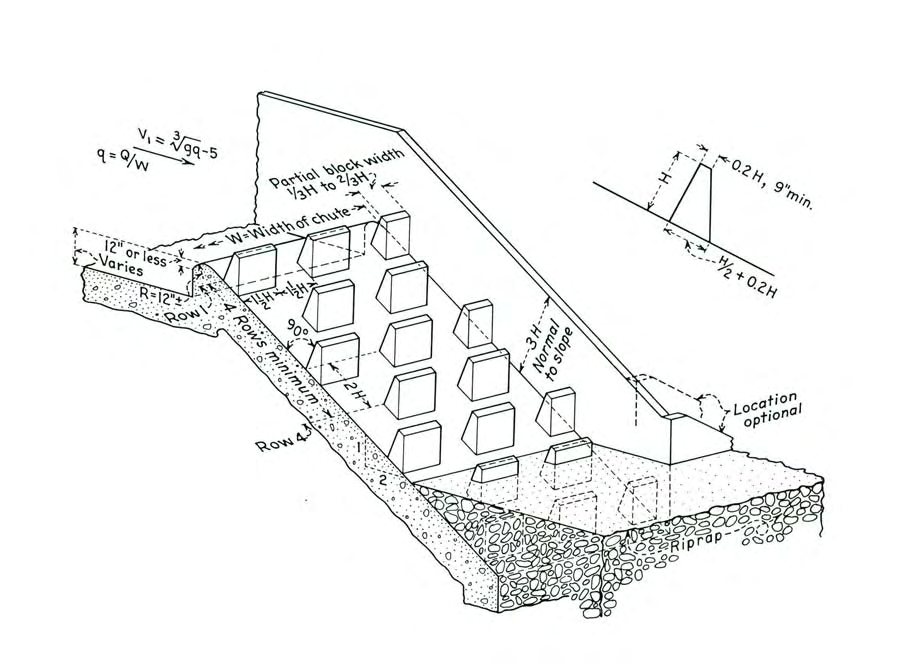
USBR Type IX baffled apron bị giới hạn trong các điều kiện hiện trường và giới hạn thiết kế sau:
- Độ dốc cống/máng không lớn hơn 50 phần trăm (1:2) và không nhỏ hơn 25 phần trăm (1:4).
- Lưu lượng đơn vị nhỏ hơn hoặc bằng 5.6 m³/s/m (60 ft³/s/ft).
- Vận tốc tiếp cận nhỏ hơn vận tốc tới hạn (số Froude trước khi rơi nhỏ hơn 1).
Baffled apron không phải là cấu trúc nhằm làm chậm vận tốc tiếp cận quá lớn, mà nhằm ngăn ngừa sự gia tốc quá mức trong quá trình rơi theo phương thẳng đứng. Theo Peterka (1978), vận tốc tiếp cận khuyến nghị nên thấp hơn vận tốc tới hạn 1.5 m/s (5 ft/s). Các vận tốc gần hoặc vượt vận tốc tới hạn có xu hướng làm dòng chảy bị nẩy lên không khi va vào hàng baffle đầu tiên và vượt qua hai hoặc ba hàng baffle đầu. Điều này đặc biệt đáng lo ngại đối với các apron có chiều dài tương đối ngắn. Một chiến lược để giảm vận tốc tiếp cận là tạo một đoạn tiếp cận hạ thấp trước đầu vào của apron như minh họa trong Hình 7.9.
Một yếu tố thiết kế quan trọng khác là lựa chọn kích thước baffle (chiều cao, chiều rộng và khoảng cách). Dựa trên các thử nghiệm mô hình và quan sát từ mẫu thực tế của Peterka, chiều cao baffle, H, nên bằng khoảng 0.8 lần chiều sâu tới hạn, \(y_c\). Chiều cao có thể tăng lên đến 0.9\(y_c\), nhưng không được nhỏ hơn 0.8\(y_c\).
Như thể hiện trong Hình 7.9, chiều rộng baffle và khoảng cách ngang giữa các baffle nên bằng 1.5H, nhưng không được nhỏ hơn H. Mỗi hàng nên được bố trí xen kẽ, và có thể cần các khối baffle dạng một phần ở các vách bên của cống hoặc máng.
Khoảng cách dọc giữa các hàng baffle được dựa trên giả định độ dốc của apron là 50% (dốc tối đa). Trong điều kiện này, các hàng baffle liên tiếp được bố trí cách nhau 2H tính theo phương dọc dốc. Đối với các baffle có chiều cao nhỏ hơn 0.9 m (3 ft), khoảng cách giữa các hàng có thể lớn hơn 2H, nhưng không vượt quá 1.8 m (6 ft). Với các độ dốc apron nhỏ hơn 50%, khoảng cách dọc theo dốc có thể được tăng lên sao cho độ cao rơi thẳng đứng giữa các hàng baffle là 0.89H.
Cần có bốn hàng baffle để kiểm soát hoàn toàn dòng chảy, mặc dù ít hàng hơn cũng đã từng thành công. Như minh họa trong Hình 7.9, máng thường được kéo dài xuống dưới mức đáy của kênh xả, với hàng baffle thấp hơn được chôn xuống để kiểm soát xói. Đá riprap kích cỡ 6 đến 12 inch nên được đặt tại đầu cuối phía hạ lưu của các vách bên để ngăn sự xói lở do xoáy nước gây ra, nhưng không nên mở rộng quá nhiều vào trong lòng kênh.
Quy trình thiết kế USBR Type IX baffled apron có thể được tóm tắt theo các bước sau:
Bước 1.
Tính toán điều kiện dòng chảy chuẩn trong cống/máng để xác định xem điều kiện xả tại cửa ra có cần được giảm nhẹ hay không.
Bước 2.
Xác minh rằng điều kiện dòng chảy tiếp cận là chấp nhận được.
Bước 3.
Tính toán vận tốc xả. Nếu vận tốc này thỏa mãn tiêu chí, thì USBR Type IX có thể là một phương án tiêu tán năng lượng phù hợp.
Bước 4.
Xác định chiều cao baffle, khoảng cách và các chi tiết thiết kế khác.
nd: một số hình ảnh sưu tầm về Baffled Apron USBR Type IX
Hình minh họa các kỹ thuật thi công được sử dụng trên hai máng có baffle và hoạt động của một máng khác ở mức công suất một phần. Trong bức ảnh sau, một lượng nhỏ đá riprap đặt trên bờ đất có thể đã ngăn chặn được hiện tượng xói lở và trượt đất mềm ở đầu hạ lưu của bức tường dẫn bên phải.



nguồn: A WATER RESOURCES TECHNICAL PUBLICATION; ENGINEERING MONOGRAPH No. 25
Ví dụ thiết kế: USBR Type IX Baffled Apron (Hệ SI)
Thiết kế một USBR Type IX baffled apron để tiêu tán năng lượng trong một cống hộp bê tông với tổng chiều cao rơi thẳng đứng là 8 m. Xác định xem vận tốc tại cửa ra có nhỏ hơn 3 m/s hay không.
Cho:
Q=2.8 m3/s; D=1.2 m; B=1.2 m
Kênh tiếp cận: n=0.020; \(S_o\)=0.01m/m
Cống/Máng: n= 0.013; \(S_o\)=0.333m/m
Giải:
Bước 1.
Tính điều kiện dòng chảy normal trong cống/máng để xác định xem có cần thiết kế baffled apron hay không. Sử dụng phương pháp thử và sai cùng với quan hệ hình học từ các Phương trình 7.11, 7.12 và 7.13:
- \(y_n = 0.19 \, \text{m}\)
- \(V_n = 12.2 \, \text{m/s}\) (Vì lớn hơn 3 m/s nên cần tiêu tán năng lượng.)
Bước 2.
Xác minh rằng điều kiện dòng chảy tiếp cận là chấp nhận được. Ước tính điều kiện dòng tiếp cận bằng phương pháp thử và sai và phương trình Manning:
- \(y_n = 0.92 \, \text{m}\)
- \(V_n = 2.54 \, \text{m/s}\)
So sánh vận tốc tiếp cận này với vận tốc tới hạn tính theo công thức:
- \(q = Q/B = 2.8 / 1.2 = 2.33 \, \text{m}^3/\text{s}/\text{m}\)
- \(V_c = (qg)^{1/3} = (2.33 \cdot 9.8)^{1/3} = 2.84 \, \text{m/s}\)
Vì \(V_c > V_n\) (vận tốc tiếp cận) và lưu lượng đơn vị nhỏ hơn 5.6 m³/s/m, nên baffled apron là phù hợp.
Bước 3.
Tính vận tốc xả. Vận tốc xả không được vượt quá một phần ba vận tốc tới hạn; trong trường hợp này:
- Vận tốc xả = 2.84/3=0.95 m/s
Giá trị này nhỏ hơn nhiều so với yêu cầu thiết kế là 3 m/s, do đó USBR Type IX là phương pháp tiêu tán năng lượng phù hợp.
Bước 4.
Xác định chiều cao, khoảng cách và các đặc điểm thiết kế khác của baffle. Trước tiên, cần tính chiều sâu tới hạn:
- \(y_c = q / V_c = 2.33 / 2.84 = 0.82 \, \text{m}\)
- Chiều cao baffle, \(H = 0.8 y_c = 0.8(0.82) = 0.66 \, \text{m}\)
- Chiều rộng baffle = \(1.5H = 1.5(0.66) = 0.99 \, \text{m}\)
- Khoảng cách baffle theo phương ngang = \(1.5H = 0.99 \, \text{m}\)
- Độ cao rơi thẳng đứng giữa các hàng baffle, \(\Delta h = 0.89H = 0.89(0.66) = 0.59 \, \text{m}\)
- Khoảng cách dọc (đo dọc theo apron) giữa các hàng baffle, \(L = 1.87 \, \text{m}|)
- Chiều cao tối thiểu của vách bên = \(H = 3(0.66) = 1.98 \, \text{m}\)
(Vì đây là một cống kín với chiều cao thành là 1.2 m, hiện tượng bắn tóe không phải là vấn đề.)
Tóm tắt kết quả thiết kế:
- 13 hàng baffle, h=0.66 mh = 0.66 \, \text{m}
- Chiều dài apron = 25.3 m
- Vận tốc tại cửa ra = 0.95 m/s (giảm vận tốc 92%)
7.4 Cống gẫy khúc (broken-back culvert)/Điều chỉnh cửa xả
Một phương án thay thế cho việc lắp đặt cống có độ dốc lớn là phá vỡ độ dốc thành một đoạn dốc hơn gần cửa vào, tiếp theo là một đoạn runout nằm ngang. Cấu hình này được gọi là broken-back culvert và có thể được xem là một chiến lược tiêu tán năng lượng nội bộ (tích hợp) khác nếu được thiết kế sao cho xảy ra một cú nhảy thủy lực (hydraulic jump) trong đoạn runout để tiêu tán năng lượng. Hình 7.10 minh họa hai trường hợp: một broken-back culvert kép và một broken-back culvert đơn. Trong cả hai trường hợp, đoạn xả hoặc runout được giả định là nằm ngang. Dưới các điều kiện nhất định về đặc tính cống và mực nước hạ lưu, một cú nhảy thủy lực sẽ xảy ra trong đoạn runout và làm giảm vận tốc đầu ra từ trạng thái siêu tới hạn về mức tương ứng với độ sâu sequent. Các điều chỉnh trong đoạn runout có thể được sử dụng để tạo ra cú nhảy thủy lực bên trong cống.
7.4.1 Thủy lực cống gãy khúc
Một cú nhảy thủy lực sẽ hình thành trong kênh nếu xảy ra một trong hai điều kiện sau:
(1) động lượng của dòng chảy hạ lưu sau cống lớn hơn trong thân cống, hoặc
(2) số Froude siêu tới hạn trong thân cống giảm xuống xấp xỉ 1.7 trong môi trường dòng chảy chậm dần (Chow, 1959).
Để giải bài toán thủy lực của broken-back culvert, một profile mặt nước biến đổi dần được tính toán trong cống từ cửa vào đến đoạn runout nằm ngang. Profile dòng siêu tới hạn này được so sánh với cao trình nước hạ lưu và độ sâu sequent để xác định liệu cú nhảy thủy lực có xảy ra trong đoạn runout hay không.
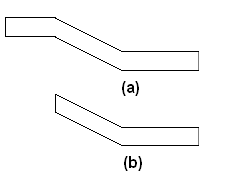
Nếu một cú nhảy xảy ra, thiết kế phải đảm bảo rằng cú nhảy đó bị giới hạn trong đoạn runout. Trước tiên, cần xác định vị trí của cú nhảy tính từ đầu đoạn runout. Việc này được thực hiện bằng cách tính các profile thượng lưu và hạ lưu của cú nhảy để tìm vị trí mà động lượng bằng nhau, tức là vị trí cú nhảy xảy ra.
Thứ hai, chiều dài của cú nhảy được ước tính. Tổng của hai giá trị này (vị trí và chiều dài cú nhảy) phải nhỏ hơn chiều dài đoạn runout. Chiều dài cú nhảy đối với cống hoặc kênh hình chữ nhật được tính theo công thức:
$$L = 220(y_1)\tanh\left(\frac{Fr – 1}{22}\right) \tag{7.25}$$
trong đó:
- L = chiều dài cú nhảy, m (ft)
- \(y_1\) = độ sâu dòng chảy siêu tới hạn, m (ft)
- Fr = số Froude siêu tới hạn
Đối với cống hình tròn, chiều dài cú nhảy bằng sáu lần độ sâu sequent dưới tới hạn, trong đó độ sâu sequent được tính bằng công thức thực nghiệm (French, 1985).
Việc phân tích thủy lực của broken-back culverts đã được đơn giản hóa nhờ ứng dụng máy tính có tên Broken-back Computer Analysis Program, hay BCAP (Hotchkiss và cộng sự, 2004).
Thiết kế được khuyến nghị giới hạn trong các điều kiện sau:
- Độ dốc của đoạn dốc lớn phải nhỏ hơn hoặc bằng 1.4:1 (V:H)
- Cú nhảy thủy lực phải hoàn tất bên trong thân cống
(nd: 1.4:1)
1.4:1 (V:H) tương đương với 140% độ dốc
Góc nghiêng khoảng 54.5 độ so với phương ngang
Trong các trường hợp mà đoạn runout quá ngắn và/hoặc không có đủ mực nước hạ lưu (tailwater) để hoàn tất (hoặc khởi phát) cú nhảy bên trong thân cống, có thể thực hiện các điều chỉnh tại cửa xả để tạo ra cú nhảy. Hai phương án điều chỉnh sẽ được trình bày trong các phần tiếp theo.
7.4.2 Outlet Weir (Cửa xả có ngưỡng tràn)
Đặt một weir gần cửa xả của cống sẽ tạo ra một cú nhảy thủy lực trong một số điều kiện dòng chảy nhất định (xem Hình 7.11). Weir này bố trí trên toàn bộ bề rộng của cống hộp và được đặt cách cửa xả khoảng 3 m (10 ft) về phía thượng lưu. Vị trí này giúp loại bỏ rác từ phía thượng lưu của weir. Các lỗ thoát trong weir ngăn nước bị ứ đọng ở thượng lưu. Khoảng cách \(L_w\) được đo từ điểm thay đổi độ dốc (nơi kết thúc đoạn dốc) đến vị trí weir trong đoạn runout. Chiều cao của cống tại vị trí đặt weir phải lớn hơn \(y_2\).
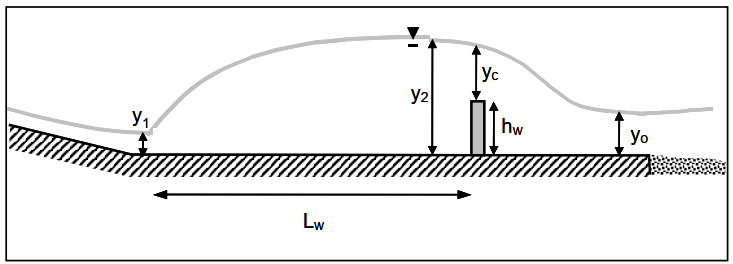
Các weir kiểu này được thiết kế để sử dụng kết hợp với broken-back culverts, nhưng cũng có thể sử dụng cho máng. Chúng được đặt trong đoạn runout nằm ngang phía hạ lưu từ điểm thay đổi độ dốc thoát ra khỏi đoạn dốc, với khoảng cách sẽ được xác định trong quá trình thiết kế. Loại weir này hoạt động tốt nhất khi không có mực nước đọng hoặc mực nước hạ lưu thiết kế phía sau cống. Vì dòng chảy sẽ đi qua weir mà không có ảnh hưởng giảm thiểu từ mực nước hạ lưu, dòng chảy sẽ đi qua độ sâu tới hạn và trở thành siêu tới hạn khi đến gần cửa xả của cống. Nhu cầu bảo vệ đáy kênh phía hạ lưu sẽ giảm nhờ sự hiện diện của weir.
Hotchkiss và cộng sự (2005) đã thử nghiệm các điều kiện tương tự với nghiên cứu của Forster và Skrinde (1950). Các weir gần cửa ra của cống sẽ tạo ra các cú nhảy thủy lực khi số Froude của dòng tiếp cận nằm trong khoảng từ 2 đến 7. Các kỹ sư thiết kế quan tâm đến cấu trúc tiêu năng này cũng có thể tham khảo thêm thiết kế các bể tiêu năng ở Chương 8.
Thiết kế được khuyến nghị giới hạn trong các điều kiện sau:
- Số Froude dòng tiếp cận nằm trong khoảng từ 2 đến 7
- Chiều cao weir nằm trong khoảng từ \(0.7y_1 đến 4.2y_1\)
- Cống hình chữ nhật
Điều kiện thủy lực dòng tiếp cận có thể được xác định cho broken-back culverts (xem Mục 7.4) hoặc cho các máng hoặc bất kỳ đoạn dốc nào nối đến một đoạn runout nằm ngang. Tuy nhiên, quy trình thiết kế sau đây chỉ mới được phát triển cho mặt cắt hình chữ nhật. Các phần mở rộng trong tương lai của phương pháp này sẽ cần được hỗ trợ bởi các thử nghiệm bổ sung.
Quy trình này sử dụng độ sâu tới hạn và độ sâu sequent cho cú nhảy thủy lực. Độ sâu tới hạn đối với cống hình chữ nhật đã được trình bày trước đó tại Phương trình 7.1. Độ sâu sequent được tính như sau:
$$y_2 = \frac{y_1}{2} \left( \sqrt{1 + 8Fr_1^2} – 1 \right) \tag{7.26}$$
trong đó:
- \(y_2\) = độ sâu sequent, m (ft)
Thiết kế weir chủ yếu liên quan đến việc lựa chọn vị trí và chiều cao của nó. Mối quan hệ giữa chiều cao weir, độ sâu dòng tiếp cận và số Froude được cho bởi:
$$h_w = \left(0.033Fr_1^2 + 0.4385Fr_1 – 0.6534\right)y_1 \tag{7.27}$$
trong đó:
- \(h_w\) = chiều cao weir, m (ft)
- \(y_1\) = độ sâu tại đầu đoạn runout, m (ft)
Khoảng cách từ điểm thay đổi độ dốc đến weir, xấp xỉ bằng chiều dài cú nhảy thủy lực, được tính như sau:
$$L_w = 5y_2 \tag{7.28}$$
Phương trình 7.28 dựa trên dữ liệu thực nghiệm. Vì lý do này và do tính đơn giản của nó, phương trình này được sử dụng trong quy trình thiết kế thay vì Phương trình 7.25.
Để tính toán các điều kiện phía hạ lưu của weir, gần cửa ra của cống, cần phải giải phương trình năng lượng theo phương pháp lặp để xác định độ sâu phía sau weir, giả định không có tổn thất năng lượng:
$$h_w + y_c + \left( \frac{Q}{By_c} \right)^2 \frac{1}{2g} = y_3 + \left( \frac{Q}{By_3} \right)^2 \frac{1}{2g} \tag{7.29}$$
trong đó:
- \(y_3\) = độ sâu lý thuyết tại cửa ra cống, m (ft)
- B = bề rộng cống, m (ft)
Phương trình 7.29 có hai nghiệm: dòng dưới tới hạn (subcritical) và dòng siêu tới hạn (supercritical). Lời giải siêu tới hạn được chọn vì sau khi dòng vượt qua độ sâu tới hạn tại ngưỡng tràn (weir), nó sẽ chuyển sang trạng thái siêu tới hạn.
Độ sâu lý thuyết sau đó được điều chỉnh để phản ánh tổn thất năng lượng, dựa trên dữ liệu thực nghiệm của Hotchkiss et al. (2005):
$$y_o = 1.23y_3 + \alpha \tag{7.30}$$
trong đó:
- \(y_o\) = độ sâu tại cửa ra, m (ft)
- α = hằng số hiệu chỉnh tổn thất năng lượng:
- α=0.015 m (hệ SI)
- α=0.05 ft (hệ CU)
Vận tốc tại cửa ra tương ứng được tính theo công thức:
$$V_o = \frac{Q}{By_o} \tag{7.31}$$
Quy trình thiết kế sau đây có thể được sử dụng:
Bước 1.
Tìm độ sâu dòng chảy \(y_1\), vận tốc và số Froude tại đầu đoạn runout nằm ngang.
(Thông số này có thể được tính bằng phần mềm BCAP (Hotchkiss et al. 2004), HY8 (phần mềm phân tích cống của FHWA), hoặc các công cụ tính toán khác để xác định độ sâu tại đầu vào đoạn runout.)
Bước 2.
Tìm độ sâu tới hạn \(y_c\) bằng Phương trình 7.1.
Bước 3.
Xác định chiều cao weir (Phương trình 7.27) và vị trí đặt weir (Phương trình 7.28).
Bước 4.
Giải phương trình năng lượng (Phương trình 7.29) theo phương pháp lặp để tìm độ sâu ở hạ lưu của weir.
Bước 5.
Tính độ sâu tại cửa ra (Phương trình 7.30) và vận tốc cửa ra (Phương trình 7.31). Đánh giá xem mức tiêu tán năng lượng có đạt yêu cầu không. Kiểm tra chiều cao cống có đủ để đảm bảo khoảng không vận hành.
Ví dụ thiết kế: Cửa xả có ngưỡng tràn (Outlet Weir) trong cống hộp (Hệ SI)
Thiết kế một outlet weir trong đoạn runout của một cống hộp bê tông cốt thép (RCB) và xác định các điều kiện tại cửa ra.
Độ sâu dòng tiếp cận vào đoạn runout là \(y_1 = 0.375 \, \text{m}.\)
Cho:
Q=14.2 m3/s
D=2.44 m
B=4.3 m
Giải:
Bước 1.
Tìm độ sâu dòng chảy \(y_1\), vận tốc và số Froude tại đầu đoạn runout nằm ngang. \(y_1\) đã cho.
$$\begin{aligned} V_1 &= \frac{Q}{B y_1} = \frac{14.2}{(4.3)(0.375)} = 8.81 \, \text{m/s} \\ Fr_1 &= \frac{V_1}{\sqrt{g y_1}} = \frac{8.81}{\sqrt{9.81(0.375)}} = 4.6 \end{aligned}$$
Bước 2.
Tìm độ sâu tới hạn \(y_c\) theo Phương trình 7.1.
Lưu lượng riêng \(\frac{Q}{B} = \frac{14.2}{4.3} = 3.302 \, \text{m}^2/\text{s}\)
$$y_c = \left( \frac{q^2}{g} \right)^{1/3} = \left( \frac{3.302^2}{9.81} \right)^{1/3} = 1.036 \, \text{m}$$
Bước 3.
Tính chiều cao weir theo Phương trình 7.27 và vị trí theo 7.28:
\(\begin{aligned} h_w &= \left(0.033Fr_1^2 + 0.4385Fr_1 – 0.6534\right)y_1 \\ &= \left(0.0331(4.6)^2 + 0.4385(4.6) – 0.6534 \right)(0.375) \\ &= 0.774 \, \text{m} \end{aligned}\)
Tính độ sâu sequent \(y_2\) theo 7.26:
\(\begin{aligned} y_2 &= \frac{y_1}{2} \left( \sqrt{1 + 8Fr_1^2} – 1 \right) \\ &= \frac{0.375}{2} \left( \sqrt{1 + 8(4.6)^2} – 1 \right) = 2.255 \, \text{m} \end{aligned}\)
Khoảng cách đặt weir:
\(L_w = 5 y_2 = 5(2.255) = 11.27 \, \text{m} \approx 11.3 \, \text{m}\)
Bước 4.
Giải phương trình năng lượng (7.29) bằng phương pháp thử và sai → \(y_3 = 0.561 \, \text{m}\)
Bước 5.
Tính độ sâu tại cửa ra:
\(\begin{aligned} y_o &= 1.23 y_3 + \alpha = 1.23(0.561) + 0.015 = 0.705 \, \text{m} \\ V_o &= \frac{Q}{B y_o} = \frac{14.2}{4.3(0.705)} = 4.7 \, \text{m/s} \end{aligned}\)
Đánh giá:
Nếu vận tốc này chấp nhận được, thiết kế weir là phù hợp. Ngoài ra, cần kiểm tra rằng độ sâu trong cống không chạm đỉnh cống. Với chiều cao cống là 2.44 m > chiều cao nhảy (2.25 m), thiết kế là chấp nhận được.
7.4.3 Outlet Drop Followed by a Weir (Cửa xả kết hợp bậc/ngưỡng tràn)
Một bậc hạ thấp đáy cống (drop) tiếp theo là một weir được thể hiện trong Hình 7.12. Tương tự như weir đặt gần cửa ra của cống (Mục 7.5), cấu hình này được dùng kết hợp với một broken-back culvert hoặc máng, nơi mà một đoạn dốc lớn kết thúc bằng một đoạn runout nằm ngang. Vị trí của drop tính từ điểm gãy dốc trong đoạn ống dốc, \(L_d\), vào khoảng 1.5 m (5 ft).
Drop có tác dụng làm giảm hiệu quả độ dốc của đoạn cống dốc, trong khi weir tạo ra cú nhảy thủy lực giữa drop và weir. Drop cũng có thể được sử dụng trong trường hợp chiều cao của cú nhảy thủy lực trong thiết kế tại Mục 7.5 chạm đến đỉnh cống.
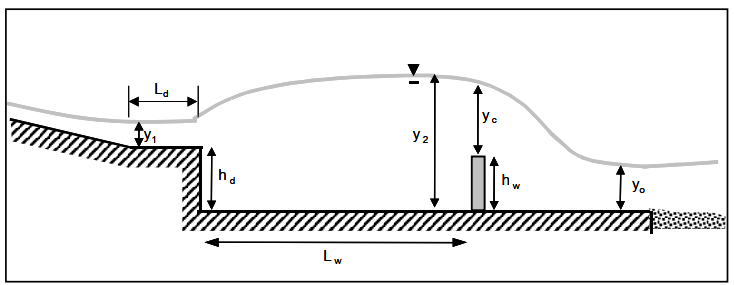
Quy trình thiết kế được xây dựng dựa trên Hotchkiss và Larson (2004) và Hotchkiss et al. (2005).
Một tập hợp lớn các thí nghiệm đã được thực hiện nhằm xác định mức giảm năng lượng, động lượng và vận tốc tại cửa ra của cống do sự hiện diện của một cấu hình drop tiếp theo là weir. Các kết quả thực nghiệm đưa ra mối quan hệ giữa chiều cao drop \(h_d\), số Froude dòng tiếp cận và chiều cao weir. Các kỹ sư thiết kế quan tâm đến cấu hình này cũng có thể so sánh kết quả với cấu trúc drop thẳng đứng (xem Mục 11.1) tại cuối cống hoặc máng.
Thiết kế được khuyến nghị giới hạn trong các điều kiện sau:
- Số Froude dòng tiếp cận từ 3.5 đến 6
- Tỷ số chiều cao weir so với độ sâu dòng tiếp cận \((h_w / y_1)\) nằm trong khoảng từ 1.3 đến 4
- Chiều cao drop bằng 60% đến 65% chiều cao của weir (đề xuất, không bắt buộc)
- Cống hình chữ nhật
Các điều kiện thủy lực tại vị trí 1 có thể được xác định cho broken-back culverts (xem Mục 7.4) hoặc cho các máng hoặc bất kỳ đoạn dốc nào nối với đoạn runout nằm ngang. Tuy nhiên, quy trình thiết kế dưới đây chỉ được phát triển cho tiết diện hình chữ nhật. Các phần mở rộng trong tương lai của phương pháp này cần được hỗ trợ bằng các thí nghiệm bổ sung.
Quy trình sử dụng độ sâu tới hạn và độ sâu sequent cho cú nhảy thủy lực. Độ sâu tới hạn cho cống hình chữ nhật đã được nêu trong Phương trình 7.1. Độ sâu sequent đã được đưa ra trước đó ở Phương trình 7.26.
Việc thiết kế weir chủ yếu liên quan đến việc chọn vị trí và chiều cao. Mối quan hệ giữa chiều cao weir, độ sâu dòng tiếp cận và số Froude được cho bởi Phương trình 7.32. Chiều cao weir cũng liên quan đến chiều cao drop:
$$h_w = \frac{h_d}{h_w} \left( 0.9326Fr_1^2 – 6.8218Fr_1 + 14.859 \right) y_1 \tag{7.32}$$
trong đó:
- \(h_w\) = chiều cao weir, m (ft)
- \(h_d\) = chiều cao drop, m (ft)
- \(y_1\) = độ sâu tại đầu đoạn runout, m (ft)
Để giải Phương trình 7.32, tỷ số \(h_d/h_w\) được chọn nằm trong khoảng từ 0.60 đến 0.65.
Khoảng cách từ điểm drop đến weir được tính như sau:
$$L_w = 6(y_c + h_w) \tag{7.33}$$
Giá trị \((y_c + h_w)\) xấp xỉ độ sâu sequent phía sau một cú nhảy thủy lực cổ điển.
Để tính toán điều kiện ở hạ lưu của weir, gần cửa ra của cống, cần giải phương trình năng lượng (Equation 7.29) theo phương pháp lặp để xác định độ sâu tại hạ lưu của weir, giả sử không có tổn thất năng lượng. Phương trình 7.29 đã được trình bày trước đó được dùng cho mục đích này. Độ sâu lý thuyết tính từ phương trình 7.29 được điều chỉnh theo tổn thất năng lượng dựa trên dữ liệu thực nghiệm của Hotchkiss et al. (2005) bằng cách sử dụng Phương trình 7.30 đã trình bày trước đó.
Quy trình thiết kế sau có thể được sử dụng:
Bước 1.
Xác định độ sâu dòng chảy \(y_1\), vận tốc, và số Froude tại đầu đoạn runout nằm ngang.
(Thông số này có thể tính bằng phần mềm BCAP (Hotchkiss et al. 2004), HY8 (phần mềm phân tích cống của FHWA), hoặc công cụ tính toán khác.)
Bước 2.
Tính độ sâu tới hạn \(y_c\) theo Phương trình 7.1.
Bước 3.
Tính chiều cao weir (Phương trình 7.32), vị trí weir (Phương trình 7.33), và chiều cao drop.
Bước 4.
Giải phương trình năng lượng (Phương trình 7.29) theo phương pháp lặp để tìm độ sâu tại hạ lưu của weir.
Bước 5.
Tính độ sâu tại cửa ra (Phương trình 7.30) và vận tốc tại cửa ra (Phương trình 7.31).
Đánh giá mức tiêu tán năng lượng và kiểm tra chiều cao cống có đảm bảo khoảng không tự do hay không.
Ví dụ thiết kế: Drop và Outlet Weir trong cống hộp (SI)
Thiết kế một outlet weir trong đoạn runout của một cống hộp bê tông cốt thép (RCB) và xác định các điều kiện tại cửa ra. Độ sâu dòng tiếp cận vào đoạn runout là \(y_1 = 0.375 \, \text{m}\).
Cho:
Q=14.2 m3/s
D=2.44 m
B=4.3 m
Giải:
Bước 1.
Tìm độ sâu dòng chảy \(y_1\), vận tốc và số Froude tại đầu đoạn runout nằm ngang. \(y_1\) đã cho.
\(V_1 = \frac{Q}{B y_1} = \frac{14.2}{(4.3)(0.375)} = 8.81 \, \text{m/s}\)
\(Fr_1 = \frac{V_1}{\sqrt{g y_1}} = \frac{8.81}{\sqrt{9.8 \cdot 0.375}} = 4.6\)
Bước 2.
Tính độ sâu tới hạn \(y_c\) theo Phương trình 7.1.
\(q = \frac{Q}{B} = \frac{14.2}{4.3} = 3.302 \, \text{m}^2/\text{s}\)
\(y_c = \left( \frac{q^2}{g} \right)^{1/3} = \left( \frac{3.302^2}{9.81} \right)^{1/3} = 1.036 \, \text{m}\)
Bước 3.
Tính chiều cao weir, vị trí và chiều cao drop.
Chọn tỉ số \(\frac{h_d}{h_w} = 0.64\)
\(\begin{aligned} h_w &= \frac{h_d}{(0.9326 Fr_1^2 – 6.8218 Fr_1 + 14.859)} y_1 \\ &= 0.64 (0.9326(4.6)^2 – 6.8218(4.6) + 14.859)(0.375) = 0.771 \, \text{m} \end{aligned}\)
Tính độ sâu sequent \(y_2\):
\(y_2 = \frac{y_1}{2} \left( \sqrt{1 + 8Fr_1^2} – 1 \right) = \frac{0.375}{2} \left( \sqrt{1 + 8(4.6)^2} – 1 \right) = 2.255 \, \text{m}\)
Tính khoảng cách từ drop đến weir:
\(L_w = 6(y_c + h_w) = 6(1.036 + 0.771) = 10.87 \approx 10.9 \, \text{m}\)
Tính chiều cao drop:
\(h_d = 0.64 \cdot h_w = 0.64 \cdot 0.771 = 0.49 \, \text{m}\)
Bước 4.
Giải phương trình năng lượng (Phương trình 7.29) theo phương pháp thử và sai để tìm độ sâu tại hạ lưu của weir. Qua quá trình thử, thu được: \(y_3 = 0.568 \, \text{m}\)
Bước 5.
Tính độ sâu tại cửa ra (Phương trình 7.30) và vận tốc tại cửa ra (Phương trình 7.31). Đánh giá mức tiêu tán năng lượng.
\(\begin{aligned} y_o &= 1.23 y_3 + \alpha = 1.23(0.568) + 0.015 = 0.714 \, \text{m} \\ V_o &= \frac{Q}{B y_o} = \frac{14.2}{4.3 \cdot 0.714} = 4.7 \, \text{m/s} \end{aligned}\)
Đánh giá:
Nếu vận tốc này là chấp nhận được thì thiết kế weir là phù hợp. Đồng thời, cần kiểm tra rằng độ sâu trong cống không chạm đến đỉnh cống. Trong trường hợp này, chiều cao cống (2.44 m) lớn hơn chiều cao cú nhảy trừ đi độ cao drop: 2.25 m−0.49 m=1.76 m<2.44 m
=> Thiết kế là chấp nhận được.
Hỗ trợ duy trì trang:
Tôi xây dựng trang này để chia sẻ các tài liệu kỹ thuật cốt lõi trong thiết kế hạ tầng giao thông.
Nếu bạn thấy nội dung hữu ích và muốn góp phần duy trì trang hoạt động bền vững, tôi rất trân trọng mọi sự ủng hộ.