A.1 Giới thiệu
Phụ lục này bao gồm các phương trình inlet control được sử dụng để xây dựng các biểu đồ thiết kế trong tài liệu này.
- Mục A.2 trình bày các phương trình cho trường hợp cửa vào không ngập và bị ngập.
- Mục A.3 minh họa cách sử dụng các phương trình trong Mục A.2 để xây dựng các đường thiết kế không thứ nguyên cho các hình dạng culvert với hệ số (Mục A.3.1) và không có hệ số (Mục A.3.2).
- Mục A.4 thảo luận cách sử dụng các đường thiết kế không thứ nguyên để phát triển các biểu đồ trong Phụ lục C.
- Mục A.5 trình bày cách sử dụng các đường thiết kế không thứ nguyên để phát triển các phương trình đa thức được sử dụng trong phần mềm FHWA.
A.2 Các phương trình Inlet Control
Các phương trình được sử dụng để xây dựng các biểu đồ inlet control trong Phụ lục C được dựa trên các nghiên cứu của Cục Tiêu chuẩn Quốc gia Hoa Kỳ (NBS) dưới sự tài trợ của Cục Đường bộ Công cộng (nay là Cơ quan Quản lý Đường cao tốc Liên bang – FHWA). John L. French của NBS đã công bố bảy báo cáo tiến độ từ nghiên cứu này. Trong đó, báo cáo đầu tiên (NBS 1955) và thứ tư (NBS 1961) đến thứ bảy (NBS 1966a, 1966b, 1967) nghiên cứu thủy lực của culvert dạng ống và hộp có và không có cửa vào dạng thuôn. Herbert G. Bossy của FHWA đã tổng hợp nghiên cứu này trong tài liệu “Hydraulics of conventional Highway Culverts” (Bossy 1961). Thông tin nền tảng bổ sung được tìm thấy trong tài liệu HEC-13 (FHWA 1972a) và các ghi chú nội bộ chưa công bố (Bossy 1963 và Normann 1974).
Hai điều kiện cơ bản của inlet control phụ thuộc vào việc đầu vào của culvert có bị ngập bởi mực nước thượng lưu hay không:
- Nếu không bị ngập, cửa vào hoạt động như một đập tràn, áp dụng các phương trình chưa bị ngập (Mục A.2.1).
- Nếu bị ngập, cửa vào hoạt động như một lỗ thoát (orifice), áp dụng các phương trình bị ngập (Mục A.2.2).
Giữa hai trạng thái chưa bị ngập và đã bị ngập là một vùng chuyển tiếp mà NBS chỉ cung cấp thông tin hạn chế. Vùng này được xác định thực nghiệm bằng cách vẽ một đường cong nối giữa các đường cong định nghĩa các phương trình đã và chưa bị ngập. Trong hầu hết các trường hợp, vùng chuyển tiếp này là ngắn và đường cong dễ xác định.
A.2.1 Phương trình Inlet Control khi cửa vào không ngập
Phương trình chưa bị ngập có hai dạng:
- Dạng (1) dựa trên cao áp cụ thể tại độ sâu tới hạn, được hiệu chỉnh với các hệ số.
- Dạng (2) là phương trình lũy thừa tương tự như phương trình đập tràn.
Dạng (1) được ưu tiên về mặt lý thuyết, trong khi dạng (2) dễ áp dụng hơn và là dạng duy nhất được ghi nhận cho một số phương trình inlet control.
Các phương trình (A.1) và (A.2) chỉ áp dụng cho Q/AD0.5 = 3.5 (1.93 SI).
Dạng (1) $$ \frac{HW_i}{D} = \frac{H_c}{D} + K \left( \frac{K_u Q}{AD^{0.5}} \right)^M + K_s S \tag{A.1} $$
Dạng (2): $$ \frac{HW_i}{D} = K \left[ \frac{K_u Q}{AD^{0.5}} \right]^M \tag{A.2}$$
Trong đó:
- HWi: Độ sâu mực nước thượng lưu tính từ đáy (invert) của tiết diện kiểm soát tại cửa vào, ft (m)
- D: Chiều cao trong của thân culvert, ft (m)
- Hc: Cột áp cụ thể tại độ sâu tới hạn \( (d_c + V_c^2 / 2g) \), ft (m)
- Q: Lưu lượng, ft³/s (m³/s)
- A: Diện tích toàn phần tiết diện dòng chảy của culvert, ft² (m²)
- S: Độ dốc thân culvert, ft/ft (m/m)
- K,M,c,Y: Các hằng số từ Bảng A.1, A.2, A.3
- Ku: Hệ số chuyển đổi đơn vị 1.0 (1.811 SI)
- Ks: Hệ số hiệu chỉnh độ dốc, -0.5 (với mitered inlets +0.7)
A.2.2 Phương trình inlet control khi cửa vào bị ngập
Phương trình áp dụng cho trường hợp bị ngập (A.3) được dùng khi Q/AD0.5 ≈ 4.0 (2.21 SI).
Các thành phần trong phương trình được định nghĩa ở Mục A.2.1.
$$\frac{HW_i}{D} = c \left[ \frac{K_u Q}{AD^{0.5}} \right]^2 + Y + K_s S \tag{A.3}$$
A.3 Đường thiết kế không thứ nguyên cho Inlet Control
Các phương trình ở Mục A.2 có thể được dùng để xây dựng đường thiết kế cho bất kỳ hình dạng hoặc kích thước culvert nào. Khi kiểm tra kỹ các hằng số trong cùng một dạng phương trình cho thấy sự khác biệt nhỏ giữa các cấu hình cửa vào cụ thể. Vì vậy, khi có thông số hình học cần thiết từ nhà sản xuất cho một hình dạng mới, có thể chọn một hình dạng tương tự và sử dụng các hằng số tương ứng để phát triển đường thiết kế mới.
Các đường này có thể gần như không thứ nguyên, ví dụ dưới dạng Q/AD0.5 và HWi/D; hoặc có thể có thứ nguyên, dưới dạng Q và HWi cho một kích thước ống cụ thể. Để đường cong thật sự không thứ nguyên, Q/AD0.5 cần được chia cho g0.5, tuy nhiên sẽ tạo ra các giá trị thập phân nhỏ.
Lưu ý: Các hệ số cho hình dạng hộp (rectangular) không nên được sử dụng cho các hình dạng không phải hộp (tròn, mái vòm, vòm hình ống…) và ngược lại. Một giá trị độ dốc cố định là 2% (0.02) thường được chọn để phát triển các đường thiết kế vì hiệu ứng độ dốc là nhỏ và giá trị mực nước thượng lưu kết quả thường bị đánh giá cao hơn (trừ trường hợp cửa vào dạng mitered inlets). Quy trình này được minh họa ở Mục A.3.1.
A.3.1 Ví dụ: Culvert có kết cấu dạng bản, hình ellipse
Phát triển đường thiết kế không thứ nguyên cho culvert bản kết cấu hình ellipse, với trục ngang dài hơn trục đứng. Giả định cửa vào là loại nhô ra mỏng (thin wall projecting inlet).
Sử dụng các hệ số và số mũ cho culvert kim loại dạng mái vòm có gợn sóng, hình dạng tương tự ellipse.
Từ Bảng A.1, Chart 34, Scale 3:
- Trường hợp chưa ngập: Phương trình dạng (1) với K = 0.0340 và M = 1.5
- Trường hợp bị ngập: c = 0.0496 và Y = 0.53
Chưa ngập, phương trình Dạng 1 (Phương trình A.1):
$$\frac{HW_i}{D} = \frac{H_c}{D} + 0.0340 \left( \frac{Q}{AD^{0.5}} \right)^{1.5} – (0.5)(0.02)$$
Đã ngập (Phương trình A.3):
$$\frac{HW_i}{D} = 0.0496 \left( \frac{Q}{AD^{0.5}} \right)^2 + 0.53 – (0.5)(0.02)$$
Một mối quan hệ trực tiếp giữa HWi/D và Q/AD0.5 có thể được xác định cho điều kiện bị ngập.
Đối với điều kiện chưa ngập, cần xác định lưu lượng và chiều cao cột áp tại độ sâu tới hạn. Tại độ sâu tới hạn, chiều cao cột áp do vận tốc tới hạn bằng một nửa độ sâu thủy lực.
$$\frac{V_c^2}{2g} = \frac{y_h}{2} = \frac{A_p}{2T_p}$$
Do đó, chiều cao cột áp tại độ sâu tới hạn chia cho D là:
$$\frac{H_c}{D} = \frac{d_c}{D} + \frac{y_h}{2D} \tag{A.4}$$
Vì số Froude bằng 1.0 tại độ sâu tới hạn, Vc có thể được xác định từ phương trình Froude và được sử dụng trong phương trình liên tục để giải cho Qc
$$F_r = \frac{V_c}{(g y_h)^{0.5}} = 1 \qquad V_c = \frac{Q_c}{A_p} = (g y_h)^{0.5} \qquad Q_c = A_p (g y_h)^{0.5}, \text{ hoặc} $$
$$\frac{Q_c}{AD^{0.5}} = \frac{A_p}{A} \left( g \cdot \frac{y_h}{D} \right)^{0.5} \tag{A.5}$$
Từ dữ liệu hình học do nhà sản xuất cung cấp cho ống ellipse nằm ngang (Kaiser 1984), các thông số hình học cần thiết được dùng để tính toán \( H_c/D \text{ và } Q_c/AD^{0.5}\)
| \(d_c/D\) | \(y_h/D\) | (Phương trình A.4) \(H_c/D\) | \(A_p/A\) | (Phương trình A.5) \(Q_c/AD^{0.5}\) |
|---|---|---|---|---|
| 0.1 | 0.04 | 0.12 | 0.04 | 0.05 |
| 0.2 | 0.14 | 0.27 | 0.14 | 0.30 |
| 0.4 | 0.30 | 0.55 | 0.38 | 1.18 |
| 0.6 | 0.49 | 0.84 | 0.64 | 2.54 |
| 0.8 | 0.85 | 1.22 | 0.88 | 4.60 |
| 0.9 | 1.27 | 1.53 | 0.97 | 6.20 |
| 1.0 | — | — | 1.00 | — |
Từ phương trình chưa bị ngập và bảng trên:
| \(Q_c/AD^{0.5}\) | \(0.0340 \times (Q_c/AD^{0.5})^{1.5}\) | \(+H_c/D\) | -0.5S= | \(HW_i/D\) |
|---|---|---|---|---|
| 0.05 | 0.0004 | 0.12 | 0.01 | 0.11 |
| 0.3 | 0.0054 | 0.27 | 0.01 | 0.27 |
| 1.18 | 0.044 | 0.55 | 0.01 | 0.58 |
| 2.54 | 0.138 | 0.84 | 0.01 | 0.55 |
| 4.6 | 0.336 | 1.22 | 0.01 | 1.54 |
| 6.2 | 0.525 | 1.53 | 0.01 | 2.05 |
Đối với phương trình bị ngập, bất kỳ giá trị nào củ \(Q/AD^{0.5}\) đều có thể được chọn vì không liên quan đến độ sâu tới hạn:
| \(Q_c/AD^{0.5}\) | \(0.0496 \times (Q_c/AD^{0.5})^2\) | +Y | −0.5S= | \(HW_i/D\) |
|---|---|---|---|---|
| 1 | 0.05 | 0.53 | 0.01 | *0.57 (*chưa bị ngập) |
| 2 | 0.2 | 0.53 | 0.01 | *0.72 (*chưa bị ngập) |
| 4 | 0.79 | 0.53 | 0.01 | 1.31 |
| 6 | 1.79 | 0.53 | 0.01 | 2.31 |
| 8 | 3.17 | 0.53 | 0.01 | 3.69 |
Giá trị có dấu sao () cho biết rõ ràng thuộc trường hợp chưa bị ngập.
Ghi chú rằng các giá trị chồng lấp của HW₁/D đã được tính toán nhằm xác định vùng chuyển tiếp giữa trạng thái không bị ngập và trạng thái bị ngập của dòng chảy. Kết quả của các phép tính trên được thể hiện trong Hình A.1. Một đường chuyển tiếp được vẽ giữa các đường cong không bị ngập và bị ngập. Các tỷ lệ trong Hình A.1 là không thứ nguyên, nhưng các hình này có thể được sử dụng để phát triển các đường cong có thứ nguyên cho bất kỳ kích thước nào của ống hình elip bằng cách nhân: Q/AD⁰·⁵ với AD⁰·⁵ và HWᵢ/D với D.
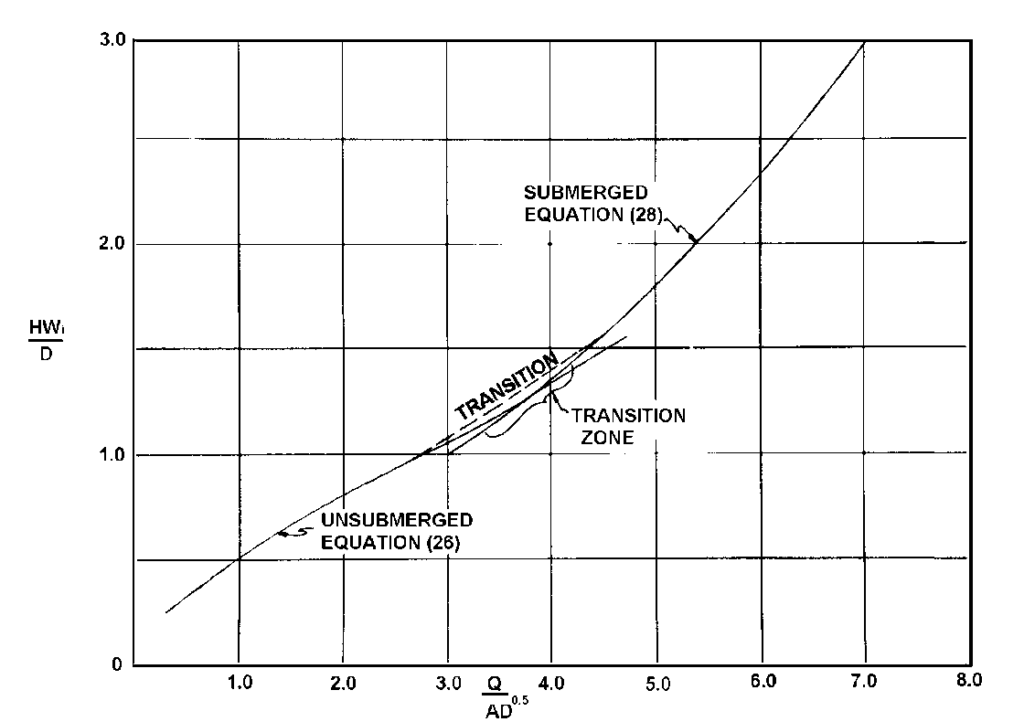
A.3.2 Biểu đồ thiết kế không thứ nguyên cho cống không cần hệ số
Các biểu đồ thiết kế inlet control không thứ nguyên được cung cấp cho vòm nhịp dài (Biểu đồ 52) và cho ống tròn và elip (Biểu đồ 51) được xây dựng bằng cách sử dụng các phương trình inlet control trong Mục A.2, các hằng số được chọn từ table A.1, hình học của ống được lấy từ các bảng và thông tin của nhà sản xuất (FHWA 1972b, Kaiser 1984, AISI 1983).
Một số kiểu cấu hình không có các thử nghiệm thủy lực. Thay vì những thử nghiệm như vậy, các điều kiện mép vào được chọn phải gần đúng với các cấu hình chưa được thử nghiệm và dẫn đến một ước lượng tốt về hiệu suất của cống. Trong một số trường hợp, sẽ cần thiết phải đánh giá cấu hình cửa vào tại một độ sâu dòng chảy cụ thể. Ví dụ, một số cửa vào có thể hành xử như cửa vào kiểu ăn sâu khi mực nước thấp và như cửa vào thành mỏng nhô ra khi mực nước cao. Kỹ sư thiết kế phải áp dụng đánh giá kỹ thuật khi lựa chọn các mối quan hệ thích hợp cho các kết cấu lớn này.
Điều kiện không bị ngập. Phương trình (A.1) được sử dụng để tính toán HWᵢ/D cho các kiểu mép vào được chọn. Các hằng số sau đây được lấy từ Table A.1, Chart 34 cho ống hình vòm, ngoại trừ cửa vào vát mép 45 độ. Các hằng số này được lấy từ Chart 3, Scale (Thang) A, cho ống tròn. Không có hằng số nào có sẵn từ các thử nghiệm trên các mô hình ống hình vòm với mép vát.
| Mép vào | K | M | KuS |
|---|---|---|---|
| Thành mỏng nhô ra (Thin Wall Projecting) | 0.0340 | 1.5 | -0.01 |
| Vát với nền đường (Mitered to Embankement) | 0.0300 | 1.0 | +0.01 |
| Mép vuông trong tường đầu (Square Edge in Headwall) | 0.0083 | 2.0 | -0.01 |
| Mép vát (vát 45°) Beveled Edge (45o Bevels) | 0.0018 | 2.5 | -0.01 |
Các mối quan hệ hình học cho ống tròn và elip (trục dài nằm ngang) được lấy từ Table 4 và 7 (FHWA 1972b). Các mối quan hệ hình học cho vòm nhịp dài kiểu cao và thấp được lấy từ DP-131 (Kaiser 1984) và các kết quả được kiểm tra chéo với các bảng trong sổ tay AISI (AISI 1983).
Điều kiện bị ngập. Phương trình (A.3) được sử dụng để tính toán HWᵢ/D cho cùng các kiểu mép vào bằng cách sử dụng các hằng số sau:
| Mép vào | c | Y | KuS |
|---|---|---|---|
| Thành mỏng nhô ra (Thin Wall Projecting) | 0.0496 | 0.53 | -0.01 |
| Vát với nền đường (Mitered to Embankement) | 0.0463 | 0.75 | +0.01 |
| Mép vuông trong tường đầu (Square Edge in Headwall) | 0.0496 | 0.57 | -0.01 |
| Mép vát (vát 45°) Beveled Edge (45o Bevels) | 0.0300 | 0.74 | -0.01 |
Xét theo Q/AD⁰·⁵, tất cả các hình dạng không chữ nhật hầu như có cùng đường cong không thứ nguyên đối với dòng chảy kiểm soát bởi cửa vào, bị ngập. Điều này không đúng nếu Q/BD¹·⁵ được sử dụng làm thông số không thứ nguyên.
Để chuyển đổi từ Q/BD¹·⁵ sang Q/AD⁰·⁵, chia cho A/B/D cho hình dạng cụ thể đang xét như trình bày trong Phương trình (A.6). Điều này giả định rằng hình dạng có hình học tương tự nhau, do đó A/BD gần như không đổi đối với một phạm vi kích thước.
$$\frac{Q/BD^{1.5}}{A/BD} = \left( \frac{Q}{BD^{1.5}} \right) \left( \frac{BD}{A} \right) = \frac{Q}{AD^{0.5}} \tag{A.6}$$
Đường cong không thứ nguyên. Bằng cách vẽ kết quả của các phép tính trong điều kiện không bị ngập và bị ngập, rồi nối các đường cong kết quả bằng các đường chuyển tiếp, các đường cong thiết kế không thứ nguyên được thể hiện trong Chart 51 và 52 của Phụ lục C đã được xây dựng. Tất cả các vòm có mặt cắt cao và thấp có thể được biểu diễn bằng một đường cong duy nhất cho mỗi cấu hình mép vào. Một tập hợp đường cong tương tự đã được phát triển cho các hình dạng tròn và elip. Khuyến nghị rằng các đường cong cho vòm cao và thấp trong Chart 52 được sử dụng cho tất cả các hình dạng vòm thực sự (tức là những hình dạng có đáy phẳng) và rằng các đường cong trong Biểu đồ 51 được sử dụng cho các hình dạng cong bao gồm hình tròn, elip, ống hình vòm và hình quả lê.
A.3.3 Biểu đồ độ sâu tới hạn không thứ nguyên
Một số cống nhịp dài và các hình dạng cống đặc biệt không có biểu đồ độ sâu tới hạn. Các hình dạng đặc biệt này có sẵn với nhiều kích thước, khiến cho việc xây dựng các đường cong độ sâu tới hạn riêng biệt cho mỗi kích thước và hình dạng cống trở nên không thực tế. Do đó, các đường cong độ sâu tới hạn không thứ nguyên đã được phát triển cho các hình dạng có mối quan hệ hình học đầy đủ trong tài liệu của nhà sản xuất. Cần lưu ý rằng các hình dạng đặc biệt này không thực sự tương đồng về mặt hình học, và bất kỳ tập hợp quan hệ hình học tổng quát nào cũng sẽ bao hàm một mức độ sai số nhất định. Mức độ sai số là không xác định vì các mối quan hệ hình học được phát triển bởi các nhà sản xuất.
Tài liệu của nhà sản xuất chứa các mối quan hệ hình học bao gồm độ sâu thủy lực chia cho chiều cao trong (độ vồng bên trong) của ống (yₕ/D) và diện tích của hình lăng trụ dòng chảy chia cho diện tích tiết diện ống (Aₚ/A) đối với các tỷ lệ độ sâu khác nhau y/D. Theo Phương trình (A.5):
$$\frac{Q}{AD^{0.5}} = \frac{A_p}{A} \left(g \cdot \frac{y_h}{D} \right)^{0.5} \tag{A.7}$$
Khi đặt y/D bằng dc/D, có thể xác định Aₚ/A và yₕ/D tại một độ sâu tương đối đã cho và sau đó tính toán Qc/AD⁰·⁵. Các đồ thị không thứ nguyên của dc/D so với Qc/AD⁰·⁵ đã được phát triển cho các vật liệu và hình dạng cống sau:
- Chart 20, corrugated metal box culverts – cống hộp kim loại gợn sóng (xem HDS 5 bản thứ hai)
- Chart 44, corrugated metal arches – vòm kim loại gợn sóng (xem HDS 5 bản thứ hai)
- Chart 53, Structural plate corrugated metal ellipses, long axis horizontal – hình elip kim loại gợn sóng, trục dài nằm ngang
- Chart 54, Structural plate corrugated metal arches, low and high profile – vòm kim loại dạng tấm, biên dạng thấp và cao
A.4 Nomograph cho Inlet Control
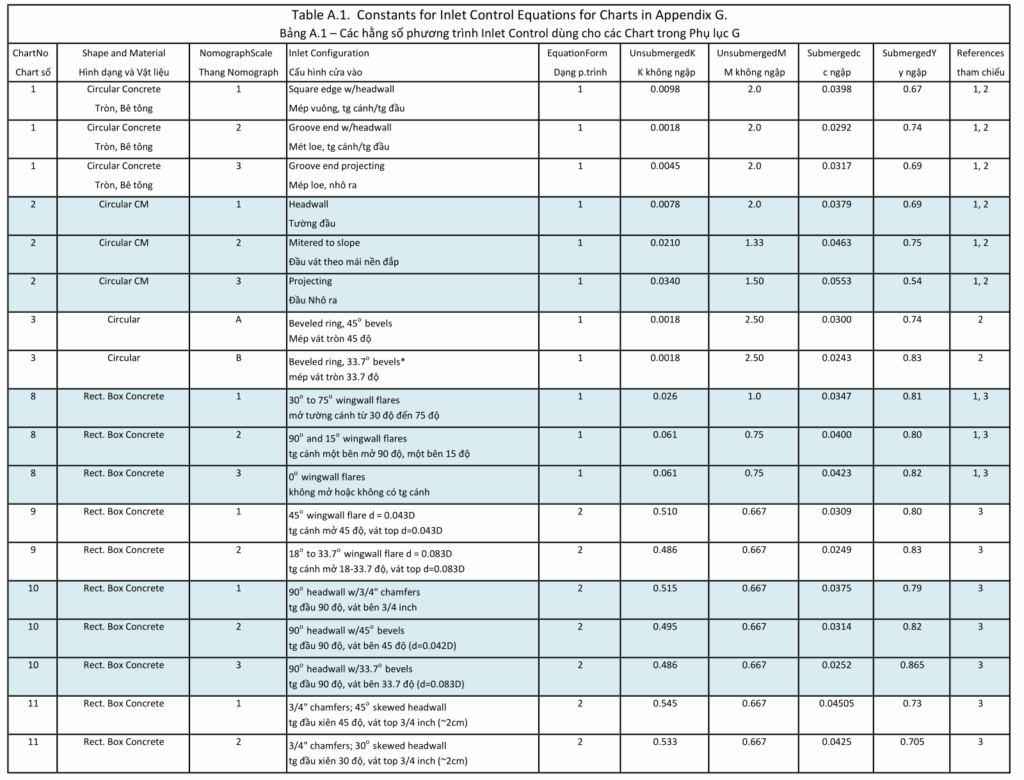
Các nomograph trong Phụ lục C được xây dựng bằng cách sử dụng các phương trình trong Mục A.2 và các hằng số được trình bày trong Table A.1. Các phương trình trong điều kiện không bị ngập và bị ngập cho một hình dạng, vật liệu và cấu hình mép vào cụ thể đã được vẽ bằng cách sử dụng quy trình đường cong thiết kế không thứ nguyên được mô tả trong Mục A.3.1. Một độ dốc cố định có giá trị 2 phần trăm (0.02) được sử dụng để phát triển các đường cong thiết kế này. Điều này là do ảnh hưởng của độ dốc là nhỏ và mực nước đầu vào (headwater) thu được là cao một cách bảo thủ (tăng độ an toàn thiết kế) đối với các vị trí có độ dốc vượt quá 2 phần trăm (trừ các cửa vào vát theo mái nền đường). Một đường cong chuyển tiếp mượt được vẽ bằng tay. Đường cong này là dữ liệu được sử dụng để xây dựng nomograph. Tiến sĩ F. T. Mavis mô tả quy trình tạo nomograph trong “The Construction of Nomographic Charts” (Mavis 1939). Các nomograph đã được sử dụng rộng rãi trong kỹ thuật trước khi máy tính vi mô được đưa vào sử dụng vào đầu những năm 1980.
Khi dùng các nomograph thiết kế cho inlet control và outlet control, một mức độ sai số nhất định được đưa vào quy trình thiết kế. Sai số này là do việc xây dựng nomograph liên quan đến các kỹ thuật lắp đồ họa, dẫn đến các Scale (thang) không khớp hoàn toàn với các phương trình. Các kiểm tra bởi các tác giả của ấn bản đầu tiên và các bên khác cho thấy tất cả các nomograph từ HEC-5 có độ chính xác ±10% so với giá trị phương trình tính theo mực nước đầu vào-headwater (trường hợp inlet control) hoặc tổn thất mực nước (trường hợp outlet control). Các nomograph cho cửa vào dạng thuôn (tapered inlet) có sai số dưới 5%, cũng tính theo mực nước đầu vào – headwater.
A.5 Phương trình Inlet Control đa thức
Các phương trình đa thức được phát triển để sử dụng trong phần mềm. Các phương trình trong Mục A.2 với các hằng số được trình bày trong các bảng hằng số cho một hình dạng, vật liệu và cấu hình mép cụ thể đã được vẽ bằng cách sử dụng quy trình đường cong thiết kế không thứ nguyên được mô tả trong Mục A.3.1. Các tọa độ của các điểm được chọn có thể được đọc từ đường cong và phân tích thống kê tốt nhất được thực hiện. Một phương trình đa thức với dạng sau được xem là phù hợp:
$$ \frac{HW_i}{D} = A + B \left[ \frac{Q}{BD^{1.5}} \right] + C \left[ \frac{Q}{BD^{1.5}} \right]^2 + \ldots + X \left[ \frac{Q}{BD^{1.5}} \right]^n + K_s S$$
Để khớp với các phương trình đa thức, Ks=0 được sử dụng cho hầu hết các phương trình để phần mềm có thể áp dụng điều chỉnh độ dốc. Hệ số dòng chảy có thể được tính dựa trên AD0.5 thay vì BD1.5. Các hằng số để khớp tốt nhất được tìm thấy trong HY-8 User Manual đi kèm với phần mềm HY-8. Đối với các phương trình bao gồm KsS, hệ số A được điều chỉnh sao cho KsS=0. HY-8 sử dụng các phương trình đa thức cho tất cả các hình dạng có hằng số được xác định trong phòng thí nghiệm hoặc bởi FHWA. Bao gồm:
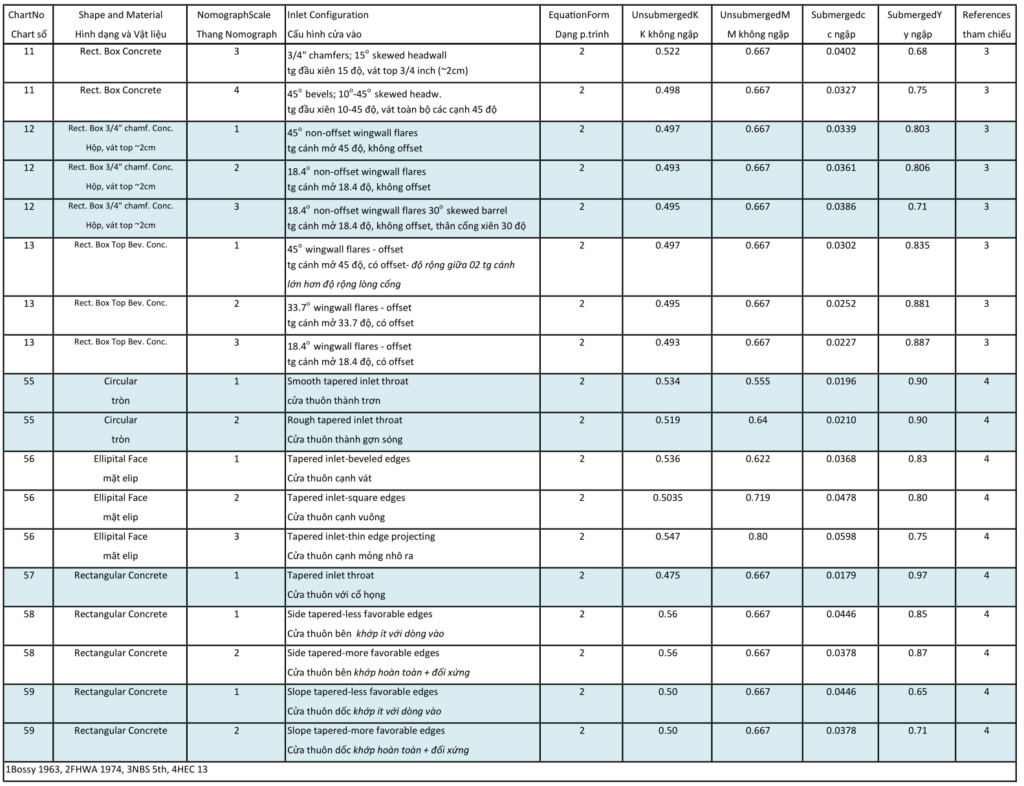
- Table A.1 – hình tròn, hộp, và cửa vào dạng thuôn (NBS, Bossy 1961)
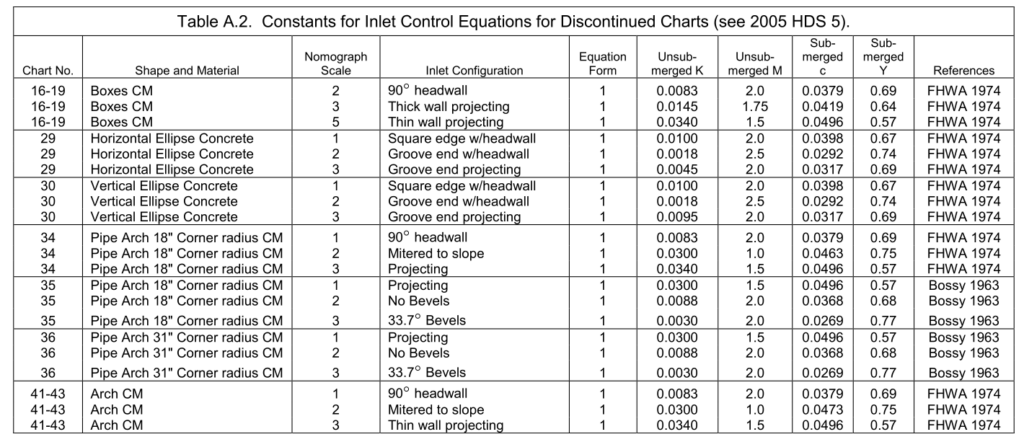
- Table A.2 – ống hình vòm, elip, hộp kim loại và vòm kim loại (Bossy 1961)
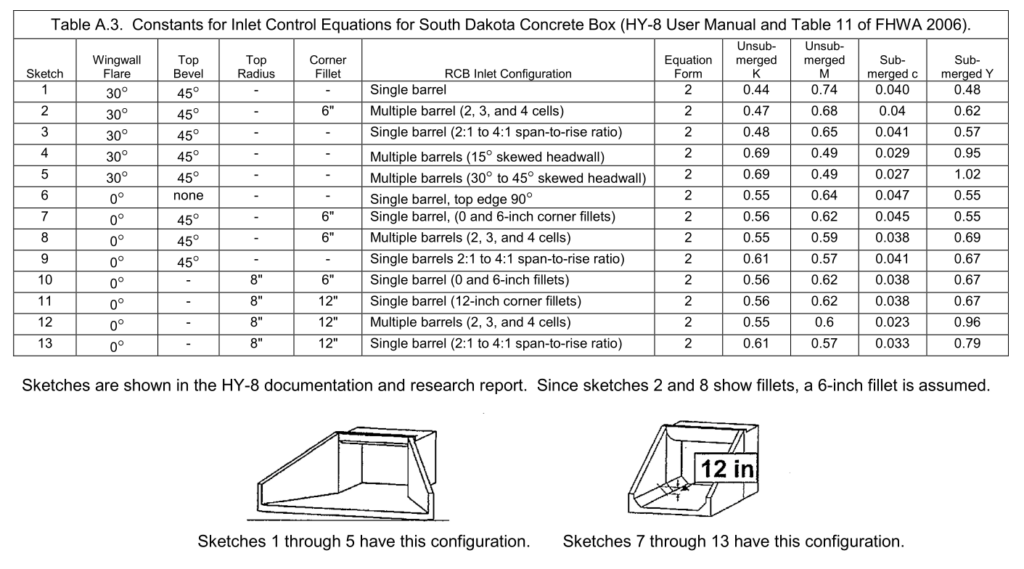
- Table A.3 – South Dakota DOT RCB (FHWA 2006c)
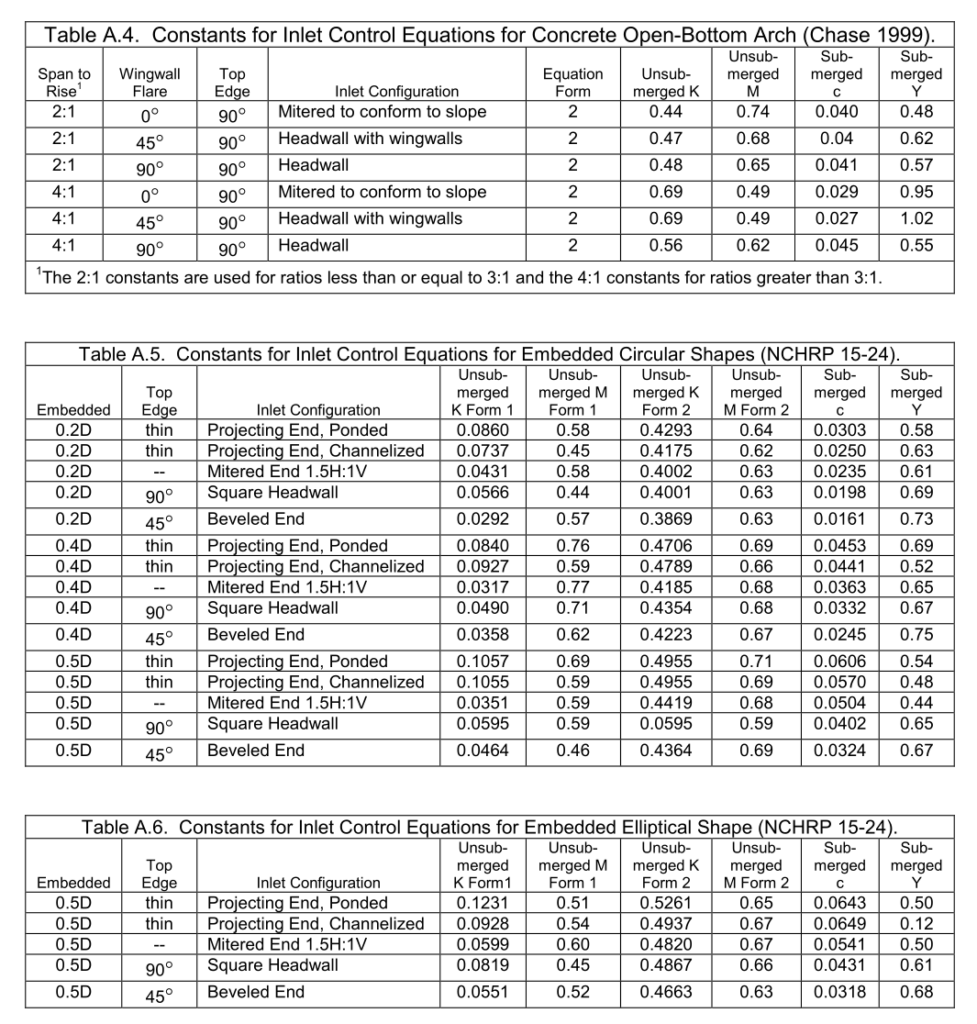
- Table A.4 – hộp bê tông đáy mở (Chase 1999)
- Table A.5 – ống tròn đặt chìm (NCHRP 2011)
- Table A.6 – hình elip đặt chìm (NCHRP 2011)
Đối với các hình dạng không có hằng số, HY-8 sử dụng Chart 52 được phát triển bằng cách sử dụng quy trình trong Mục A.3.2.
Hỗ trợ duy trì trang:
Tôi xây dựng trang này để chia sẻ các tài liệu kỹ thuật cốt lõi trong thiết kế hạ tầng giao thông.
Nếu bạn thấy nội dung hữu ích và muốn góp phần duy trì trang hoạt động bền vững, tôi rất trân trọng mọi sự ủng hộ.