Phụ lục B – Độ sâu tới hạn và dòng chảy đều đối với các hình dạng cống, kênh khác nhau

B.1 Độ sâu tới hạn mặt cắt hình chữ nhật

(nd: tính độ sâu tới hạn)

Độ sâu tới hạn cho mặt cắt chữ nhật:

$$y_c = \left( \frac{q^2}{g} \right)^{1/3}$$

trong đó:

• \(y_c\): Độ sâu tới hạn (m)
• \(q = \frac{Q}{b}\): Lưu lượng riêng (m²/s), tức là lưu lượng chia cho bề rộng đáy
• Q: Lưu lượng tổng (m³/s)
• b: Bề rộng đáy kênh chữ nhật (m)
• g: Gia tốc trọng trường (≈ 9.81 m/s²)

Ví dụ:

Cho \(Q = 10 \, \text{m}^3/\text{s}\), b=2 m

$$q = \frac{10}{2} = 5 \, \text{m}^2/\text{s}$$

$$y_c = \left( \frac{5^2}{9.81} \right)^{1/3} = \left( \frac{25}{9.81} \right)^{1/3} \approx (2.55)^{1/3} \approx 1.36 \, \text{m}$$

Độ sâu tới hạn cho mặt cắt hình thang

Đối với mặt cắt hình thang, không có công thức tường minh (explicit formula) cho độ sâu tới hạn \(y_c\) như hình chữ nhật. Tuy nhiên, có thể xác định \(y_c\) bằng phương trình năng lượng tới hạn, thường được giải bằng phương pháp lặp hoặc số.

Công thức cơ bản (để giải tìm \(y_c\):

Độ sâu tới hạn xảy ra khi mô men thuỷ lực bằng mô men động lượng, tức:

$$\frac{Q^2}{g A^3} = \frac{1}{T}$$

hoặc:

$$ Fr=1⇒ \frac{Q^2 T}{g A^3} = 1$$

trong đó:

• Q: Lưu lượng (m³/s)
• g: Gia tốc trọng trường (9.81 m/s²)
• A: Diện tích mặt cắt ướt (m²) = \(b y + z y^2\)
• T: Mặt thoáng (m) = \(b + 2 z y\)
• b: Bề rộng đáy (m)
• z: Hệ số mái (zH:1V)
• y: Độ sâu dòng chảy (sẽ là \(y_c\) khi đạt điều kiện tới hạn)

Cách làm:

1. Biểu diễn A(y)= \(b y + z y^2\)
2. Biểu diễn T(y)= \(b + 2 z y\)
3. Thế vào công thức: \(\frac{Q^2 T(y)}{g A(y)^3} = 1\)
4. Giải phương trình này bằng phương pháp lặp, ví dụ dùng Excel hoặc solver số.

Ví dụ số đơn giản:

• \(Q = 20 \, \text{m}^3/s\)
• b=4 m, z=1.5

Dùng Excel hoặc code để giải phương trình:

$$\frac{20^2 \cdot (4 + 3y)}{9.81 \cdot (4y + 1.5y^2)^3} = 1$$

Kết quả sẽ là giá trị \(y_c\) gần đúng (khoảng vài bước lặp).

Tính độ sâu Online cho mặt cắt hình thang tại đây

Độ sâu tới hạn cho mặt cắt hình tròn

Đối với mặt cắt hình tròn (ống tròn đầy hoặc không đầy), độ sâu tới hạn \(y_c\) cũng không có công thức tường minh, mà phải giải phương trình tới hạn bằng số.

Cơ sở lý thuyết:

Điều kiện tới hạn xảy ra khi: \(1Fr = 1 \Rightarrow \frac{Q^2 T(\theta)}{g A(\theta)^3} = 1\)

trong đó:

• Q: Lưu lượng (m³/s)
• g: 9.81 m/s²
• A(θ): Diện tích ướt (m²) – hàm theo góc tâm θ
• T(θ): Mặt thoáng (m) – cũng hàm theo θ
• θ: Góc ở tâm tương ứng với độ sâu dòng chảy trong ống

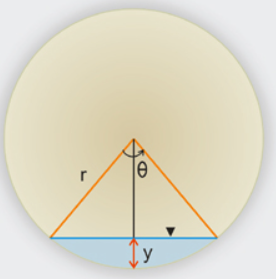
Biểu thức hình học cho ống tròn bán kính R:

Gọi θ là góc ở tâm (rad), tính từ đường nước:

• Diện tích ướt: \(A(\theta) = \frac{R^2}{2} \left( \theta – \sin \theta \right)\)
• Mặt thoáng: \(T(\theta) = 2 R \sin \left( \frac{\theta}{2} \right)\)
• Độ sâu dòng chảy (y): \(y = R (1 – \cos (\theta/2))\)

Quy trình tìm \(y_c\):

1. Chọn một bán kính ống R
2. Thử các giá trị θ∈(0,π)
3. Tính A(θ), T(θ)
4. Tính vế trái: \(\frac{Q^2 T(\theta)}{g A(\theta)^3}\)
5. Tìm θ sao cho vế trái = 1 → đó là trạng thái tới hạn
6. Tính lại \(y_c = R (1 – \cos (\theta/2))\)

Ví dụ nhanh:

Cho ống bán kính R=1 m, lưu lượng Q=2 m³/s

→ bạn có thể lập bảng trong Excel với các giá trị θ (từ 0.1 đến 3.0 rad), tính từng bước để tìm giá trị θ cho: \(\frac{Q^2 T(\theta)}{g A(\theta)^3} \approx 1\)

Khi đó, tính ra \(y_c\) theo công thức phía trên.

Tính độ sâu tới hạn Online ống tròn tại đây

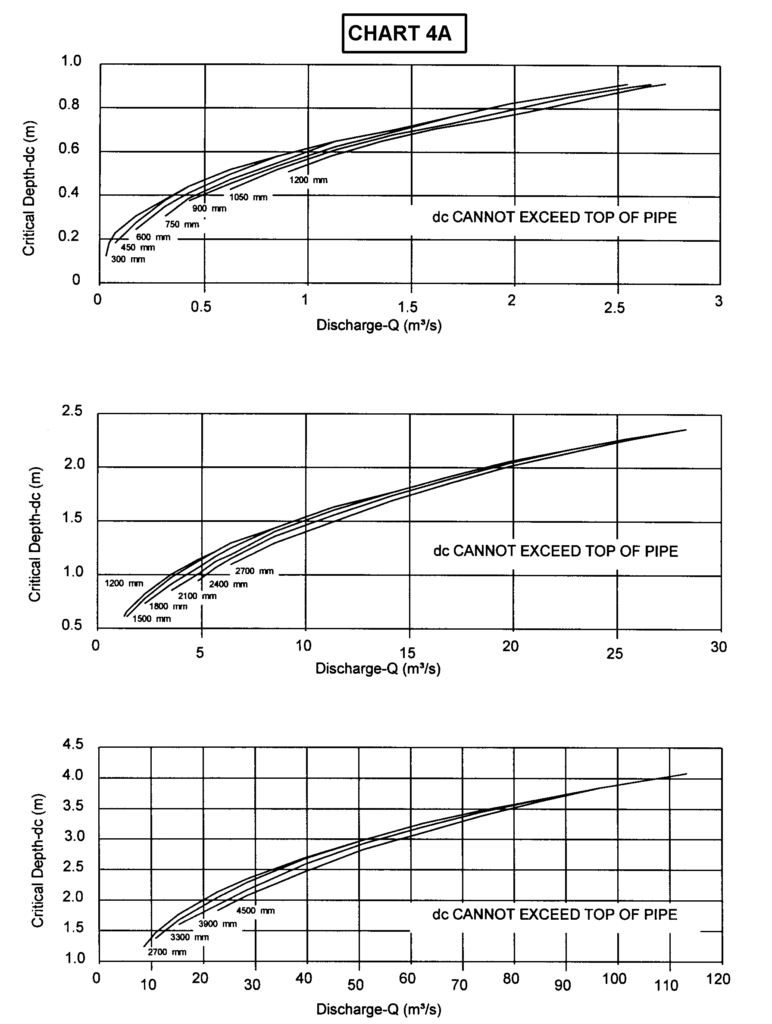
B.2 Độ sâu tới hạn cho cống tròn

B.3 Độ sâu tới hạn cho ống bê tông Oval trục dài nằm ngang

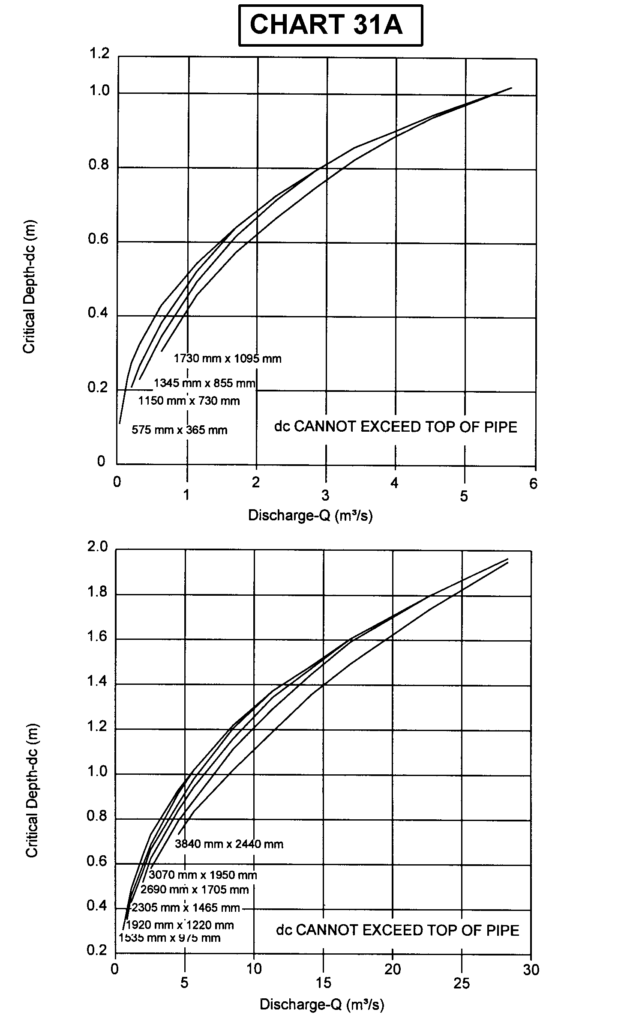
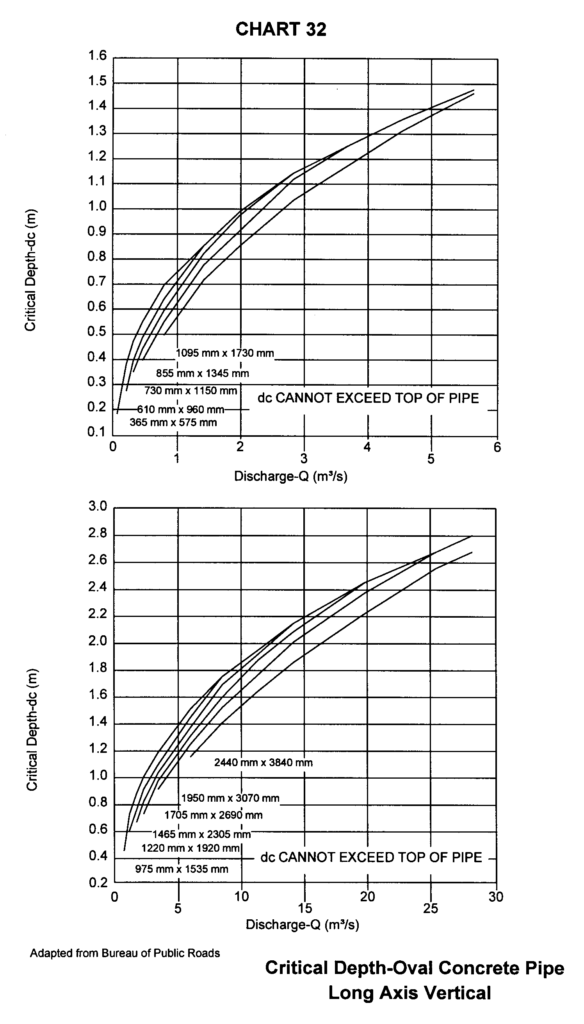
B.3 Độ sâu tới hạn cho ống bê tông Oval trục dài thẳng đứng

Bảng B.1. Dòng chảy đều trong kênh hình thang theo công thức Manning

Giá trị của (αQn)/(b^8/3S^1/2)

y/b1	z = 0	z = 0.25	z = 0.5	z = 0.75	z = 1	z = 1.25	z = 1.5	z = 1.75	z = 2	z = 3
0.02	0.00213	0.00215	0.00216	0.00217	0.00218	0.00219	0.00220	0.00220	0.00221	0.00223
0.03	0.00414	0.00419	0.00423	0.00426	0.00429	0.00429	0.00433	0.00434	0.00437	0.00443
0.04	0.00661	0.00670	0.00679	0.00685	0.00690	0.00690	0.00700	0.00704	0.00707	0.00722
0.05	0.00947	0.00964	0.00980	0.00991	0.01000	0.01010	0.01020	0.01030	0.01030	0.01060
0.06	0.0127	0.0130	0.0132	0.0134	0.0136	0.0137	0.0138	0.0140	0.0141	0.0145
0.07	0.0162	0.0166	0.0170	0.0173	0.0176	0.0177	0.0180	0.0182	0.0183	0.0190
0.08	0.0200	0.0206	0.0211	0.0215	0.0219	0.0222	0.0225	0.0228	0.0231	0.0240
0.09	0.0240	0.0249	0.0256	0.0262	0.0267	0.0271	0.0275	0.0279	0.0282	0.0296
0.10	0.0283	0.0294	0.0305	0.0311	0.0318	0.0324	0.0329	0.0334	0.0339	0.0358
0.11	0.0329	0.0342	0.0354	0.0364	0.0373	0.0380	0.0387	0.0394	0.0400	0.0424
0.12	0.0376	0.0393	0.0408	0.0420	0.0431	0.0441	0.0450	0.0458	0.0466	0.0497
0.13	0.0425	0.0446	0.0464	0.0480	0.0493	0.0505	0.0516	0.0527	0.0537	0.0575
0.14	0.0476	0.0501	0.0524	0.0542	0.0559	0.0573	0.0587	0.0599	0.0312	0.0659
0.15	0.0528	0.0559	0.0585	0.0608	0.0628	0.0645	0.0662	0.0677	0.0692	0.0749
0.16	0.0582	0.0619	0.0650	0.0676	0.0699	0.0720	0.0740	0.0759	0.0776	0.0845
0.17	0.0638	0.0680	0.0717	0.0748	0.0775	0.0800	0.0823	0.0845	0.0867	0.0947
0.18	0.0695	0.0744	0.0786	0.0822	0.0854	0.0883	0.0910	0.0936	0.0961	0.1050
0.19	0.0753	0.0809	0.0857	0.0900	0.0936	0.0970	0.1000	0.1030	0.1060	0.1170
0.20	0.0813	0.0875	0.0932	0.0979	0.1020	0.1060	0.1100	0.1130	0.1160	0.1290
0.21	0.0873	0.0944	0.1010	0.1060	0.1110	0.1150	0.1200	0.1230	0.1270	0.1420
0.22	0.0935	0.1010	0.1090	0.1150	0.1200	0.1250	0.1300	0.1340	0.1390	0.1550
0.23	0.0997	0.1090	0.1170	0.1240	0.1300	0.1350	0.1410	0.1460	0.1510	0.1690
0.24	0.106	0.116	0.125	0.133	0.139	0.146	0.152	0.157	0.163	0.184
0.25	0.113	0.124	0.133	0.142	0.150	0.157	0.163	0.170	0.176	0.199
0.26	0.119	0.131	0.142	0.152	0.160	0.168	0.175	0.182	0.189	0.215
0.27	0.126	0.139	0.151	0.162	0.171	0.180	0.188	0.195	0.203	0.232
0.28	0.133	0.147	0.160	0.172	0.182	0.192	0.201	0.209	0.217	0.249
0.29	0.139	0.155	0.170	0.182	0.193	0.204	0.214	0.223	0.232	0.267
0.30	0.146	0.163	0.179	0.193	0.205	0.217	0.227	0.238	0.248	0.286
0.31	0.153	0.172	0.189	0.204	0.217	0.230	0.242	0.253	0.264	0.306
0.32	0.160	0.180	0.199	0.215	0.230	0.243	0.256	0.269	0.281	0.327
0.33	0.167	0.189	0.209	0.227	0.243	0.257	0.271	0.285	0.298	0.348
0.34	0.174	0.198	0.219	0.238	0.256	0.272	0.287	0.301	0.315	0.369
0.35	0.181	0.207	0.230	0.251	0.270	0.287	0.303	0.318	0.334	0.392
0.36	0.190	0.216	0.241	0.263	0.283	0.302	0.319	0.336	0.353	0.416
0.37	0.196	0.225	0.251	0.275	0.297	0.317	0.336	0.354	0.372	0.440
0.38	0.203	0.234	0.263	0.289	0.311	0.333	0.354	0.373	0.392	0.465
0.39	0.210	0.244	0.274	0.301	0.326	0.349	0.371	0.392	0.412	0.491
0.40	0.218	0.254	0.286	0.314	0.341	0.366	0.389	0.412	0.433	0.518
0.41	0.225	0.263	0.297	0.328	0.357	0.383	0.408	0.432	0.455	0.545
0.42	0.233	0.279	0.310	0.342	0.373	0.401	0.427	0.453	0.478	0.574
0.43	0.241	0.282	0.321	0.356	0.389	0.418	0.447	0.474	0.501	0.604
0.44	0.249	0.292	0.334	0.371	0.405	0.437	0.467	0.496	0.524	0.634
0.45	0.256	0.303	0.346	0.385	0.442	0.455	0.487	0.519	0.548	0.665
0.46	0.263	0.313	0.359	0.401	0.439	0.475	0.509	0.541	0.547	0.696
0.47	0.271	0.323	0.371	0.417	0.457	0.494	0.530	0.565	0.600	0.729
0.48	0.279	0.333	0.384	0.432	0.475	514.000	0.552	0.589	0.626	0.763
0.49	0.287	0.345	0.398	0.448	0.492	0.534	0.575	0.614	0.652	0.797
0.50	0.295	0.356	0.411	0.463	0.512	0.556	0.599	0.639	0.679	0.833
0.52	0.310	0.377	0.438	0.496	0.548	0.599	0.646	0.692	0.735	0.906
0.54	0.327	0.398	0.468	0.530	0.590	0.644	0.696	0.746	0.795	0.984
0.56	0.343	0.421	0.496	0.567	0.631	0.690	0.748	0.803	0.856	1.070
0.58	0.359	0.444	0.526	0.601	0.671	0.739	0.802	0.863	0.922	1.150
0.60	0.375	0.468	0.556	0.640	0.717	0.789	0.858	0.924	0.988	1.240
0.62	0.391	0.492	0.590	0.679	0.763	0.841	0.917	0.989	1.060	1.330
0.64	0.408	0.516	0.620	0.718	0.809	0.894	0.976	1.050	1.130	1.430
0.66	0.424	0.541	0.653	0.759	0.858	0.951	1.040	1.130	1.210	1.530
0.68	0.441	0.566	0.687	0.801	0.908	1.010	1.100	1.200	1.290	1.640
0.70	0.457	0.591	0.722	0.842	0.958	1.070	1.170	1.270	1.370	1.750
0.72	0.474	0.617	0.757	0.887	1.010	1.130	1.240	1.350	1.450	1.870
0.74	0.491	0.644	0.793	0.932	1.070	1.190	1.310	1.430	1.550	1.980
0.76	0.508	0.670	0.830	0.981	1.120	1.260	1.390	1.510	1.640	2.110
0.78	0.525	0.698	0.868	1.030	1.180	1.320	1.460	1.600	1.730	2.240
0.80	0.542	0.725	0.906	1.080	1.240	1.400	1.540	1.690	1.830	2.370
0.82	0.559	0.753	0.945	1.130	1.300	1.470	1.630	1.780	1.930	2.510
0.84	0.576	0.782	0.985	1.180	1.360	1.540	1.710	1.870	2.030	2.650
0.86	0.593	0.810	1.030	1.230	1.430	1.610	1.790	1.970	2.140	2.800
0.88	0.610	0.839	1.070	1.290	1.490	1.690	1.880	2.070	2.250	2.950
0.90	0.627	0.871	1.110	1.340	1.560	1.770	1.980	2.170	2.360	3.110
0.92	0.645	0.898	1.150	1.400	1.630	1.860	2.070	2.280	2.480	3.270
0.94	0.662	0.928	1.200	1.460	1.700	1.940	2.160	2.380	2.600	3.430
0.96	0.680	0.960	1.250	1.520	1.780	2.030	2.270	2.500	2.730	3.610
0.98	0.697	0.991	1.290	1.580	1.850	2.110	2.370	2.610	2.850	3.790
1.00	0.714	1.020	1.330	1.640	1.930	2.210	2.470	2.730	2.990	3.970
1.05	0.759	1.100	1.460	1.800	2.130	2.440	2.750	3.040	3.330	4.450
1.10	0.802	1.190	1.580	1.970	2.340	2.690	3.040	3.370	3.700	4.960
1.15	0.846	1.270	1.710	2.140	2.560	2.960	3.340	3.720	4.090	5.520
1.20	0.891	1.360	1.850	2.330	2.790	3.240	3.680	4.090	4.500	6.110
1.25	0.936	1.450	1.990	2.520	3.040	3.540	4.030	4.490	4.950	6.730
1.30	0.980	1.540	2.140	2.730	3.300	3.850	4.390	4.900	5.420	7.390
1.35	1.02	1.64	2.29	2.94	3.57	4.18	4.76	5.34	5.90	8.10
1.40	1.07	1.74	2.45	3.16	3.85	4.52	5.18	5.80	6.43	8.83
1.45	1.11	1.84	2.61	3.39	4.15	4.88	5.60	6.29	6.98	9.62
1.50	1.16	1.94	2.78	3.63	4.46	5.26	6.04	6.81	7.55	10.40
1.55	1.20	2.05	2.96	3.88	4.78	5.65	6.50	7.33	8.14	11.30
1.60	1.25	2.15	3.14	4.14	5.12	6.06	6.99	7.89	8.79	12.20
1.65	1.30	2.27	3.33	4.41	5.47	6.49	7.50	8.47	9.42	13.20
1.70	1.34	2.38	3.52	4.69	5.83	6.94	8.02	9.08	10.10	14.20
1.75	1.39	2.50	3.73	4.98	6.21	7.41	8.57	9.72	10.90	15.20
1.80	1.43	2.62	3.93	5.28	6.60	7.89	9.13	10.40	11.60	16.30
1.85	1.48	2.74	4.15	5.59	7.01	8.40	9.75	11.10	12.40	17.40
1.90	1.52	2.86	4.36	5.91	7.43	8.91	10.40	12.40	13.20	18.70
1.95	1.57	2.99	4.59	6.24	7.87	9.46	11.00	12.50	14.00	19.90
2.00	1.61	3.12	4.83	6.58	8.32	10.00	11.70	13.30	14.90	21.10
2.10	1.71	3.39	5.31	7.30	9.27	11.20	13.10	15.00	16.80	23.90
2.20	1.79	3.67	5.82	8.06	10.30	12.50	14.60	16.70	18.70	26.80
2.30	1.89	3.96	6.36	8.86	11.30	13.80	16.20	18.60	20.90	30.00
2.40	1.98	4.26	6.93	9.72	12.50	15.30	17.90	20.60	23.10	33.40
2.50	2.07	4.58	7.52	10.60	13.70	16.80	19.80	22.70	25.60	37.00
2.60	2.16	4.90	8.14	11.60	15.00	18.40	21.70	25.00	28.20	40.80
2.70	2.26	5.24	8.80	12.60	16.30	20.10	23.80	27.40	31.00	44.80
2.80	2.35	5.59	9.49	13.60	17.80	21.90	25.90	29.90	33.80	49.10
2.90	2.44	5.95	10.20	14.70	19.30	23.80	28.20	32.60	36.90	53.70
3.00	2.53	6.33	11.00	15.90	20.90	25.80	30.60	35.40	40.10	58.40
3.20	2.72	7.12	12.50	18.30	24.20	30.10	25.80	41.50	47.10	68.90
3.40	2.90	7.97	14.20	21.00	27.90	34.80	41.50	48.20	54.60	80.20
3.60	3.09	8.86	16.10	24.00	32.00	39.90	47.80	55.50	63.00	92.80
3.80	3.28	9.81	18.10	27.10	36.30	45.50	54.60	63.50	72.40	107
4.00	3.46	10.8	20.2	30.5	41.1	51.6	61.9	72.1	82.2	122
4.50	3.92	13.5	26.2	40.1	54.5	68.8	82.9	96.9	111	164
5.00	4.39	16.7	33.1	51.5	70.3	89.2	108	126	145	216

Chú thích:

• y: độ sâu dòng chảy
• b: bề rộng đáy
• z: hệ số mái nghiêng (zH:1V)
• Q: lưu lượng dòng chảy (m³/s)
• n: hệ số nhám Manning
• S: độ dốc đáy
• α: hệ số điều chỉnh động năng (thường lấy bằng 1 nếu không có chỉ định đặc biệt)

Người dịch: Cách tính từ công thừc dòng chảy đều trong kênh hình thang:

Phương trình Manning cho dòng chảy đều:

$$Q = \frac{1}{n} A R^{2/3} S^{1/2}$$

trong đó:

• Q: Lưu lượng (m³/s)
• n: Hệ số nhám Manning
• A: Diện tích mặt cắt ướt (m²)
• \(R = \frac{A}{P}\): Bán kính thuỷ lực (m)
• P: Chu vi ướt (m)
• S: Độ dốc đáy kênh (m/m)

Áp dụng cho kênh hình thang:

Gọi:

• b: Bề rộng đáy kênh (m)
• z: Hệ số mái nghiêng (zH:1V)
• y: Độ sâu dòng chảy (m)

Tính toán hình học:

• Diện tích ướt: \(A = b y + z y^2\)
• Chu vi ướt: \(P = b + 2 y \sqrt{1 + z^2}\)
• Bán kính thuỷ lực: \(R = \frac{A}{P} = \frac{b y + z y^2}{b + 2 y \sqrt{1 + z^2}}\)

Công thức Manning đầy đủ cho kênh hình thang:

$$Q = \frac{1}{n} \cdot \left( b y + z y^2 \right) \cdot \left( \frac{b y + z y^2}{b + 2 y \sqrt{1 + z^2}} \right)^{2/3} \cdot S^{1/2}$$

Bạn có thể dùng công thức này để:

• Tính Q khi biết y, b, z, S, n
• Hoặc ngược lại, tìm y khi biết Q — thường cần giải bằng phương pháp lặp (thử-sai)

Tính độ sâu normal trong kênh hình thang Online tại đây

Bảng B.2. Dòng chảy đều, không đầy trong ống tròn

y/D	A/D2	R/D	aQn/(D8/3S1/2)	aQn/(y8/3S1/2)		y/D	A/D2	R/D	aQn/(D8/3S1/2)	aQn/(y8/3S1/2)
0.01	0.0013	0.0066	0.00007	15.04		0.51	0.4027	0.2531	0.239	1.442
0.02	0.0037	0.0132	0.00031	10.57		0.52	0.4127	0.2562	0.247	0.415
0.03	0.0069	0.0197	0.00074	8.56		0.53	0.4227	0.2592	0.255	1.388
0.04	0.0105	0.0262	0.00138	7.38		0.54	0.4327	0.2621	0.263	1.362
0.05	0.0147	0.0325	0.00222	6.55		0.55	0.4426	0.2649	0.271	1.336
0.06	0.0192	0.0389	0.00328	5.95		0.56	0.4526	0.2676	0.279	1.311
0.07	0.0294	0.0451	0.00455	5.47		0.57	0.1626	0.2703	0.287	1.286
0.08	0.0350	0.0513	0.00604	5.09		0.58	0.4724	0.2728	0.295	1.262
0.09	0.0378	0.0575	0.00775	4.76		0.59	0.4822	0.2753	0.303	1.238
0.10	0.0409	0.0635	0.0097	4.49		0.60	0.4920	0.2776	0.311	1.215
0.11	0.0470	0.0695	0.0118	4.25		0.61	0.5018	0.2799	0.319	1.192
0.12	0.0534	0.0755	0.0142	4.04		0.62	0.5115	0.2821	0.327	1.170
0.13	0.0600	0.0813	0.0167	3.86		0.63	0.5212	0.2842	0.335	1.148
0.14	0.0668	0.0871	0.0195	3.69		0.64	0.5308	0.2862	0.343	1.126
0.15	0.0739	0.0929	0.0225	3.54		0.65	0.5405	0.2988	0.350	1.105
0.16	0.0811	0.0985	0.0257	3.41		0.66	0.5499	0.2900	0.358	1.084
0.17	0.0885	0.1042	0.0291	3.28		0.67	0.5594	0.2917	0.366	1.064
0.18	0.0961	0.1097	0.0327	3.17		0.68	0.5687	0.2933	0.373	1.044
0.19	0.0139	0.1152	0.0365	3.06		0.69	0.5780	0.2948	0.380	1.024
0.20	0.1118	0.1206	0.0406	2.96		0.70	0.5872	0.2962	0.388	1.004
0.21	0.1199	0.1259	0.0448	2.87		0.71	0.5964	0.2975	0.395	0.985
0.22	0.1281	0.1312	0.0492	2.79		0.72	0.6054	0.2987	0.402	0.965
0.23	0.1365	0.1364	0.0537	2.71		0.73	0.6143	0.2998	0.409	0.947
0.24	0.1449	0.1416	0.0585	2.63		0.74	0.6231	0.3008	0.416	0.928
0.25	0.1535	0.1466	0.0634	2.56		0.75	0.6319	0.3042	0.422	0.910
0.26	0.1623	0.1516	0.0686	2.49		0.76	0.6405	0.3043	0.429	0.891
0.27	0.1711	0.1566	0.0739	2.42		0.77	0.6489	0.3043	0.435	0.873
0.28	0.1800	0.1614	0.0793	2.36		0.78	0.6573	0.3041	0.441	0.856
0.29	0.1890	0.1662	0.0849	2.30		0.79	0.6655	0.3039	0.447	0.838
0.30	0.1982	0.1709	0.0907	2.25		0.80	0.6736	0.3042	0.453	0.821
0.31	0.2074	0.1756	0.0966	2.20		0.81	0.6815	0.3043	0.458	0.804
0.32	0.2167	0.1802	0.1027	2.14		0.82	0.6893	0.3043	0.463	0.787
0.33	0.2260	0.1847	0.1089	2.09		0.83	0.6969	0.3041	0.468	0.770
0.34	0.2355	0.1891	0.1153	2.05		0.84	0.7043	0.3038	0.473	0.753
0.35	0.2450	0.1935	0.1218	2.00		0.85	0.7115	0.3033	0.453	0.736
0.36	0.2546	0.1978	0.1284	1.958		0.86	0.7186	0.3026	0.458	0.720
0.37	0.2642	0.2020	0.1351	1.915		0.87	0.7254	0.3018	0.485	0.703
0.38	0.2739	0.2062	0.1420	1.875		0.88	0.7320	0.3007	0.488	0.687
0.39	0.2836	0.2102	0.1490	1.835		0.89	0.7384	0.2995	0.491	0.670
0.40	0.2934	0.2142	0.1561	1.797		0.90	0.7445	0.2980	0.494	0.654
0.41	0.3032	0.2182	0.1633	1.760		0.91	0.7504	0.2963	0.496	0.637
0.42	0.3130	0.2220	0.1705	1.724		0.92	0.7560	0.2944	0.497	0.621
0.43	0.3229	0.2258	0.1779	1.689		0.93	0.7612	0.2921	0.498	0.604
0.44	0.3328	0.2295	0.1854	1.655		0.94	0.7662	0.2895	0.498	0.588
0.45	0.3428	0.2331	0.1929	1.622		0.95	0.7707	0.2865	0.498	0.571
0.46	0.3527	0.2366	0.201	1.590		0.96	0.7749	0.2829	0.496	0.553
0.47	0.3627	0.2401	0.208	1.559		0.97	0.7785	0.2787	0.494	0.535
0.48	0.3727	0.2435	0.216	1.530		0.98	0.7817	0.2735	0.489	0.517
0.49	0.3827	0.2468	0.224	1.500		0.99	0.7841	0.2666	0.483	0.496
0.50	0.3927	0.2500	0.232	1.471		1.00	0.7854	0.2500	0.463	0.463

• y = độ sâu dòng chảy, m (ft)
• D = đường kính ống, m (ft)
• A = diện tích dòng chảy, m² (ft²)
• R = bán kính thủy lực, m (ft)
• Nguồn: USBR (1974)
• Q = lưu lượng theo phương trình Manning, m³/s (ft³/s)
• n = hệ số nhám Manning
• S = độ dốc đáy kênh và mặt nước
• a = hệ số chuyển đổi đơn vị = 1.49 cho hệ SI, 1 cho hệ CU (hệ Anh)

Người dịch: Cách tính trực tiếp từ công thức

Trường hợp ống tròn chảy không đầy (partly full), ta vẫn áp dụng phương trình Manning:

$$Q = \frac{1}{n} A R^{2/3} S^{1/2}$$

Nhưng vì mặt cắt không đầy, nên:

• A, R, và chu vi ướt P sẽ phụ thuộc vào góc ướt θ (góc ở tâm – radian)
• Phải biểu diễn A, P, R theo θ

1. Các biểu thức hình học cho ống tròn bán kính R:

Gọi θ: góc ở tâm tính từ mặt thoáng (radian), với θ∈(0,2π)

• Diện tích mặt cắt ướt: $$A = \frac{R^2}{2} \left( \theta – \sin \theta \right)$$
• Chu vi ướt: $$P = R \theta$$
• Bán kính thuỷ lực: $$R_h = \frac{A}{P} = \frac{R}{2} \cdot \frac{\theta – \sin \theta}{\theta}$$
• Mặt thoáng (không dùng trực tiếp trong Manning nhưng dùng trong Froude): $$T = 2R \sin\left( \frac{\theta}{2} \right)$$

2. Công thức Manning áp dụng:

$$Q = \frac{1}{n} \cdot \left[ \frac{R^2}{2} (\theta – \sin \theta) \right] \cdot \left( \frac{R}{2} \cdot \frac{\theta – \sin \theta}{\theta} \right)^{2/3} \cdot S^{1/2}$$

3. Dạng không thứ nguyên (tra bảng hoặc vẽ đường cong):

Để tổng quát hóa, thường dùng dạng không thứ nguyên: $$\frac{Q}{Q_{\text{full}}} = f(\theta)$$

trong đó \(Q_{\text{full}}\) là lưu lượng khi ống đầy. Các giá trị tỉ lệ như:

• \(\frac{A}{A_{\text{full}}}\)
• \(\frac{P}{P_{\text{full}}}\)
• \(\frac{R}{R_{\text{full}}}\)
• \(\frac{Q}{Q_{\text{full}}}\)

→ được lập bảng và vẽ biểu đồ theo y/D hoặc θ

Tính độ sâu normal trong cống tròn Online tại đây