B1 Tổng quan
Trong điều kiện kiểm soát tại cửa ra (outlet control), lực cản thủy lực của thân cống phải được tính thông qua phương trình tổn thất ma sát. Có nhiều phương trình, cả lý thuyết và thực nghiệm, được sử dụng, bao gồm phương trình Darcy và phương trình Manning. Phương trình Darcy, thể hiện trong Phương trình (B.1), là chính xác về mặt lý thuyết và được trình bày trong hầu hết các tài liệu thủy lực:
$$h_f = f \left( \frac{L}{D} \right) \left( \frac{V^2}{2g} \right) \tag{B.1}$$
trong đó:
hf = cột áp tổn thất do ma sát, ft (m)
f = hệ số ma sát Darcy
L = chiều dài ống dẫn (conduit), ft (m)
D = đường kính ống dẫn, ft (m)
V = vận tốc trung bình, ft/s (m/s)
g = gia tốc trọng trường, 32.2 ft/s² (9.8 m/s²)
Hệ số ma sát Darcy f được lấy từ biểu đồ phổ biến gọi là biểu đồ Moody, liên hệ f với số Reynolds (vận tốc dòng chảy, kích thước ống và độ nhớt chất lỏng) và độ nhám tương đối (tỷ lệ giữa kích thước phần tử nhám và kích thước ống). Để phát triển các hệ số cản cho các cấu hình nhám thành ống mới hoặc chưa được kiểm nghiệm, giá trị f có thể được xác định bằng lý thuyết và sau đó chuyển đổi thành hệ số Manning n bằng mối quan hệ trong Phương trình (B.2):
$$n = 0.0926 \, R^{1/6} \, f^{1/2} \tag{B.2}$$
R là bán kính thuỷ lực, ft
Một cuộc thảo luận đầy đủ về hệ số Darcy f, cách suy diễn, và mối liên hệ của nó với các hệ số cản khác có thể được tìm thấy trong tài liệu tham khảo (Morris và Wiggert 1972).
Phương trình Manning, một quan hệ thực nghiệm, thường được dùng để tính toán tổn thất ma sát trong thiết kế cống. Dạng phổ biến của phương trình Manning như sau:
$$V = \frac{1.486}{n} \, R^{2/3} \, S^{1/2} \tag{B.3}$$
Trong đó:
V = vận tốc trung bình của dòng chảy, ft/s (m/s)
R = bán kính thuỷ lực, ft (m)
S = độ dốc của ống dẫn, ft/ft, bằng với độ dốc của mặt nước trong dòng chảy đều
Thay thế Hf/L cho S và biến đổi lại Phương trình (B.3) sẽ cho ra Phương trình (3.4b).
Giá trị hệ số Manning nn trong Phương trình (B.3) có thể dựa trên dữ liệu thử nghiệm thủy lực hoặc các hệ số cản được tính bằng phương trình lý thuyết như Darcy, sau đó quy đổi sang hệ số Manning. Như thấy trong Phương trình (B.2), hệ số Manning n thay đổi theo kích thước ống (bán kính thủy lực) với lũy thừa 1/6 và có đơn vị là ft1/6.
Do đó, với các ống dẫn rất lớn hoặc rất nhỏ, hệ số Manning’s n nên được điều chỉnh theo kích thước ống. Hầu hết các thử nghiệm thủy lực để xác định giá trị nn của Manning được tiến hành trên các ống dẫn có kích thước vừa, với đường kính từ 2 đến 5 ft (600 đến 1500 mm), hoặc trên các kênh có bán kính thủy lực từ 1 đến 4 ft (0.3 đến 1.2 m). Với các kênh tự nhiên lớn, việc tính toán backwater thường được sử dụng để hiệu chỉnh mặt cắt mực nước theo thực tế, bằng cách điều chỉnh hệ số n phù hợp với hình dạng và độ nhám của kênh.
Việc sử dụng một giá trị Manning’s n không đổi bất kể kích thước hoặc lưu lượng ống dẫn giả định rằng hệ số này chỉ phụ thuộc vào kích thước tuyệt đối của phần tử nhám tường và không phụ thuộc vào kích thước ống dẫn hay số Reynolds. Giả định này là hợp lý với các ống dẫn nhám, nơi mà ảnh hưởng của số Reynolds là không đáng kể và mối quan hệ theo lũy thừa 1/6 của kích thước ống dẫn là hợp lệ. Do đó, phương trình Manning được chấp nhận rộng rãi đối với các kênh tự nhiên và ống dẫn có thành nhám. Với các ống dẫn trơn, các phương trình cản thực nghiệm khác như phương trình Hazen-Williams thường được sử dụng nhiều hơn.
Bảng B.1 tóm tắt hệ số nn của Manning cho các vật liệu thường dùng trong xây dựng cống. Với cống kim loại có gân, dải giá trị n phụ thuộc vào kích thước ống (xem Mục B.4). Với các loại cống khác, dải giá trị phụ thuộc vào chất lượng thi công ống dẫn (xem các Mục B.2 và B.3). Trong mọi trường hợp, người thiết kế cần đánh giá và lựa chọn giá trị phù hợp, đồng thời tham khảo các tài liệu hướng dẫn khác trong các trường hợp đặc biệt. Các bảng chi tiết về hệ số Manning’s n có trong HDS 3 (FHWA 1961) và sách Open Channel Hydraulics (Chow 1959). Với các kênh tự nhiên, người thiết kế tham khảo Bảng C.1 trong Phụ lục C và các tài liệu USGS 1967 và 1984. Các giá trị Manning’s n cho vật liệu cống thường dùng được trình bày trong các phần sau.
B2 Ống bê tông
Ống bê tông được sản xuất theo nhiều phương pháp, bao gồm quay ly tâm, đúc khô, đúc nén rung, đầm chặt và đúc ướt (ACPA 1981). Độ nhám mặt trong (ảnh hưởng đến hệ số n) thay đổi tùy theo phương pháp sản xuất. Ví dụ, phương pháp đúc nén thường tạo ra bề mặt thô hơn so với đúc ướt. Chất lượng các mối nối và sự lão hóa (do mài mòn và ăn mòn) cũng ảnh hưởng đến sức cản thủy lực của ống. Thử nghiệm trong phòng trên ống đúc nén (đường kính 24–36 in, hoặc 600–900 mm, có mối nối tốt) cho giá trị n≈0.009n (Straub et al. 1960). Các giá trị này có thể tăng lên n = 0.011 đến 0.013 khi tính đến điều kiện lắp đặt thực tế và ảnh hưởng của lão hóa. Các giá trị n trong phòng thí nghiệm cho ống bê tông được liệt kê trong Bảng B.1.
B.3 Hộp bê tông
Sức cản thủy lực của cống hộp bê tông phụ thuộc vào phương pháp sản xuất, kỹ thuật lắp đặt và tình trạng lão hóa. Cống hộp có thể được đúc sẵn hoặc đúc tại chỗ. Với cống đúc sẵn, độ nhẵn của thành cống, chất lượng mối nối và độ lão hóa ảnh hưởng đến hệ số Manning n. Với cống đúc tại chỗ, chất lượng ván khuôn, kỹ thuật thi công và thời gian sử dụng là những yếu tố quan trọng. Giá trị n đối với cống đúc tại chỗ thường dao động từ 0.012 đến 0.022 (xem HDS 3, Bảng 1 – FHWA 1961). Với cống đúc sẵn, thường giả định sử dụng các giá trị thấp hơn do điều kiện bề mặt được kiểm soát tốt hơn trong nhà máy.
B4 Cống kim loại gân
Hệ số cản thủy lực của cống kim loại có gân phụ thuộc vào hình dạng và kích thước gân, khoảng cách giữa các gân, loại mối nối, độ nhám của bu lông hoặc đinh tán, phương pháp sản xuất, kích thước ống, vận tốc dòng chảy và quá trình lão hóa. Mô tả chi tiết về sức cản thủy lực của loại cống này được trình bày trong tài liệu Hydraulic Flow Resistance Factors for Corrugated Metal Conduits (FHWA 1980). Thông tin từ tài liệu đó đã được rút gọn và đưa vào Phụ lục này. Các hệ số cản được trình bày dựa trên các tiêu chí cụ thể, bao gồm cả việc sử dụng lưu lượng đặc trưng Q/D2.5 = 4.0. Ảnh hưởng của bu lông và mối nối, nếu có, cũng được nêu rõ.
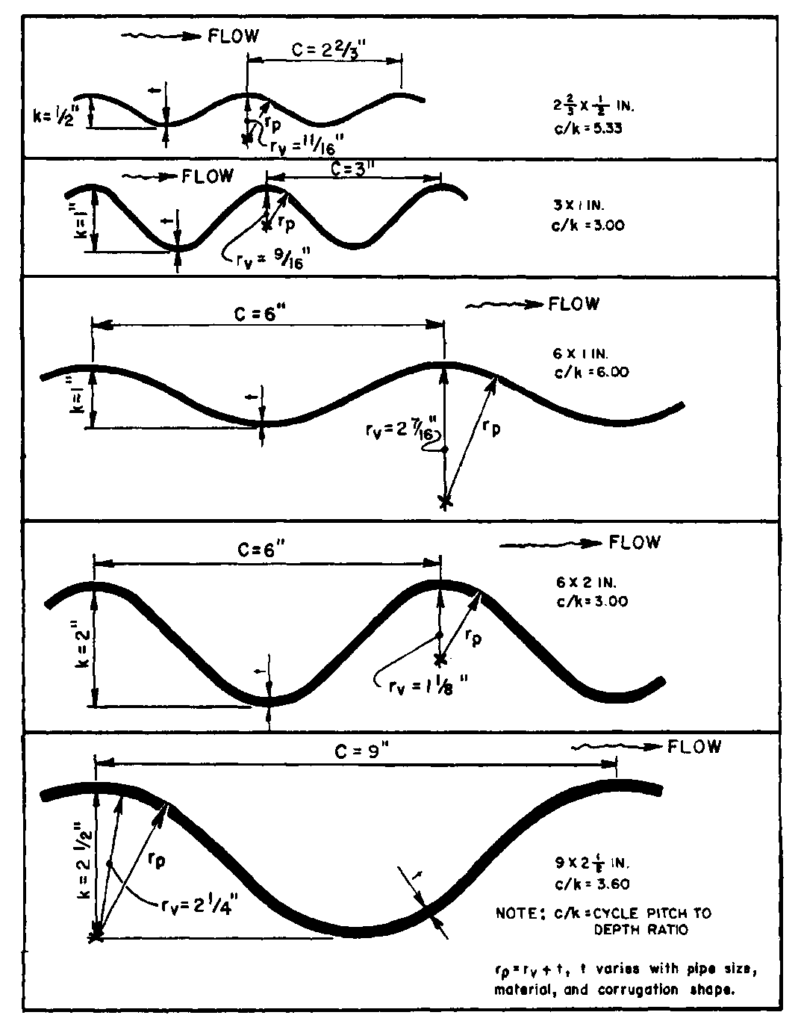
B.4.1 Gân vòng (Annular Corrugations)
Các hệ số cản đối với các dạng gân vòng được thể hiện trong Hình B-1 (FHWA 1980). Các phương pháp cũng được trình bày để ước tính sức cản thủy lực của các loại gân mới hoặc chưa được thử nghiệm. Những phương pháp này đã được sử dụng để ước tính sức cản của loại gân 5×1 inch (5 inch x 1 inch), được thể hiện trong Hình B-2, tuy nhiên hiện chưa có kết quả thử nghiệm nào cho loại này (AISI 1983).
Một loạt biểu đồ đã được xây dựng mô tả giá trị cản Manning’s nn cho nhiều dạng gân khác nhau theo các kích thước ống dẫn khác nhau (FHWA 1980). Các biểu đồ này thể hiện sự thay đổi của hệ số nn theo đường kính ống, lưu lượng và độ sâu dòng chảy. Với các ống tấm dạng kết cấu (structural plate conduits), các đường cong có thể bị gián đoạn do thay đổi số lượng tấm được sử dụng trong quá trình chế tạo. Các đường cong được trình bày cho hai mức lưu lượng: /(Q/D^{2.5} = 2.0\) và \(Q/D^{2.5} = 4.0\). Trong điều kiện thiết kế, lưu lượng chảy qua cống thường gần với đường cong ứng với \(Q/D^{2.5} = 4.0.\)
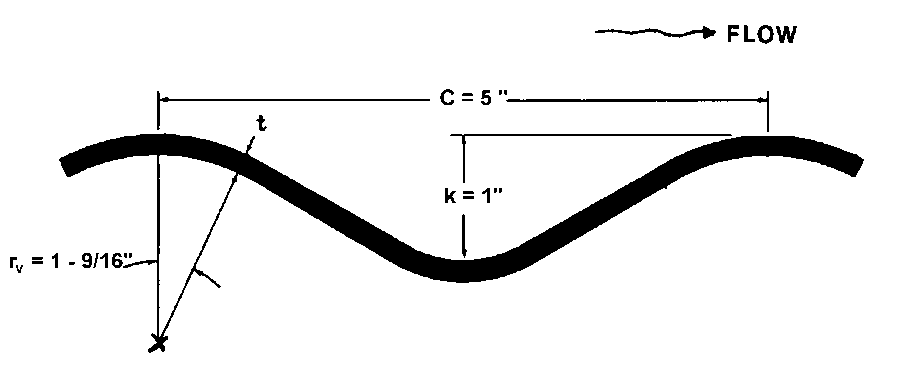
Hình B.2. Hình dạng gân 5 inch x 1 inch
Gân 5 in x 1 in là dạng gân vòng tiêu chuẩn, trong đó:
- 5 inch là khoảng cách giữa hai đỉnh gân liên tiếp (bước sóng – pitch),
- 1 inch là chiều cao của gân (từ đáy đến đỉnh sóng).
Hình B.2 thường minh họa mặt cắt ngang của một đoạn ống với các gân hình tròn đều, thể hiện rõ chiều cao gân (1 in) và bước sóng (5 in). Dạng gân này tạo ra độ nhám thành ống giúp tăng cường khả năng chịu tải và ảnh hưởng trực tiếp đến sức cản thủy lực trong tính toán hệ số Manning’s n.
B.4.2 Gân xoắn (Helical Corrugations)
Với các ống có đường kính nhỏ hơn khoảng 6 ft (1800 mm), các gân xoắn có thể cho giá trị sức cản thủy lực thấp hơn. Điều này là do dòng chảy xoáy theo hình xoắn ốc hình thành khi dòng chảy đầy trong các ống dạng này. Khi kích thước ống tăng lên, góc xoắn của gân tiến gần đến 90 độ, và hệ số Manning’s nn trở nên tương đương với loại gân vòng.
Đối với dòng chảy không đầy trong ống kim loại tròn có gân xoắn 2-2/3 in × 1/2 in (68 mm × 13 mm), hệ số Manning’s n nên được tăng thêm 11% so với giá trị dùng cho dòng chảy đầy. Trong trường hợp dòng chảy đầy qua cống hình mái vòm bằng kim loại có gân 2-2/3 in × 1/2 in (68 mm × 13 mm), hệ số Manning’s n được coi là bằng với ống có đường kính tương đương.
B.4.3 Mối quan hệ giữa hệ số Manning’s nn và đường kính ống kim loại có gân
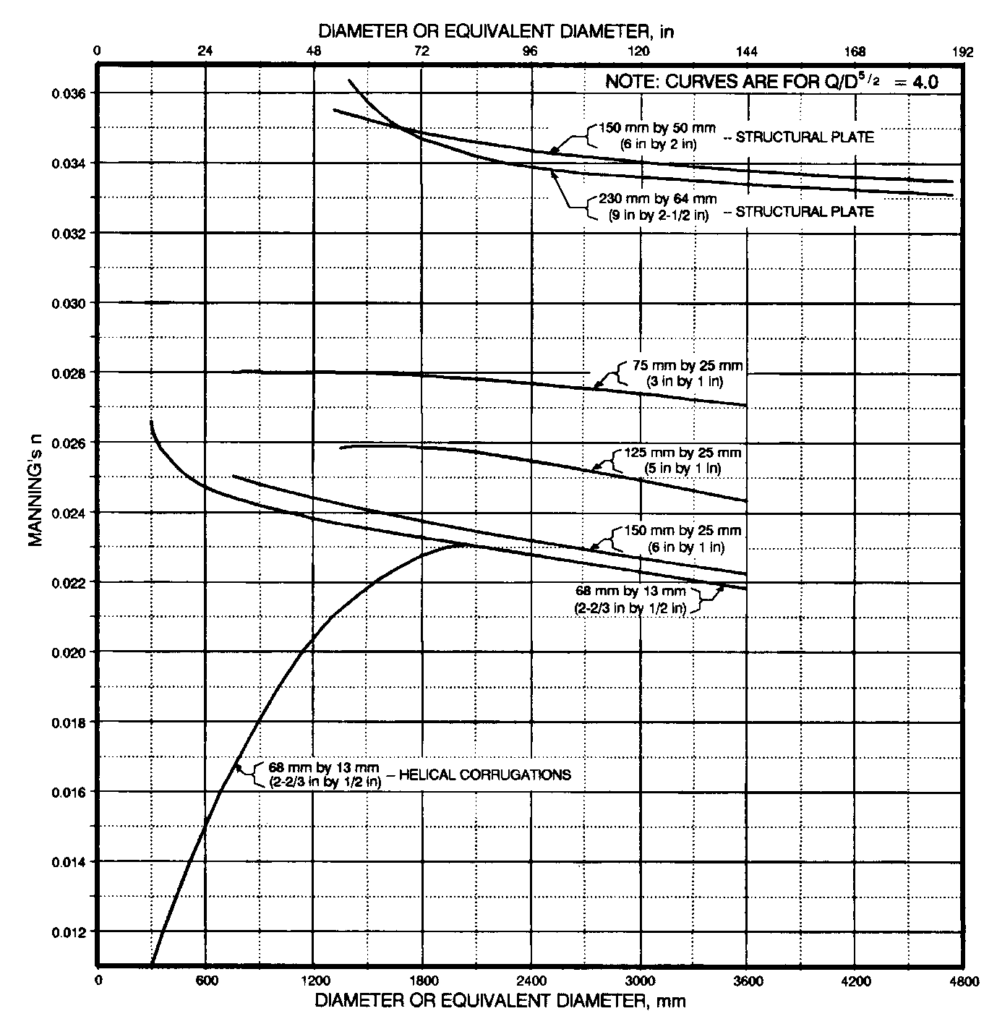
- Dựa trên các biểu đồ cho gân vòng và gân xoắn (FHWA 1980), Hình B-3 đã được xây dựng để thể hiện sự thay đổi của hệ số Manning’s nn theo đường kính ống có gân. Biểu đồ được xây dựng dựa trên giả định đơn giản hóa: các đường cong được vẽ với Q/D2.5=4.0Q/D^{2.5} = 4.0, là điều kiện thiết kế điển hình cho cống.
- Các điểm gián đoạn trong đường cong của ống thép tấm kết cấu đã được bỏ qua để thay bằng một đường cong trơn.
- Loại ống có gân xoắn duy nhất được thể hiện trong biểu đồ là loại 2-2/3 in × 1/2 in (68 × 13 mm), với chiều rộng tấm là 24 in. (600 mm).
Cách sử dụng Hình B-3: tra đường kính ống tròn theo trục ngang, sau đó đọc giá trị Manning’s nn từ đường cong tương ứng với kiểu gân.
B.5 Ống gân xoắn có sống (Spiral Rib Pipe)
Ống spiral rib là loại ống thép thành mỏng có bề mặt trơn, được chế tạo bằng đường hàn xoắn. Các yếu tố tạo nhám bao gồm các mối nối và một gân âm chạy xoắn quanh thành ống. Dựa trên thử nghiệm của các ống spiral rib đường kính 2 và 3 ft (600 đến 900 mm) (Tullis 1983), loại ống này có sức cản thủy lực gần như bằng với ống thép trơn, ngoại trừ tác động của sự lão hóa và các mối nối.
Kết quả thử nghiệm trong phòng cho thấy hệ số Manning’s nn dao động từ 0.010 đến 0.011. Có xét đến yếu tố lão hóa và kháng cản từ mối nối, hệ số Manning’s nn trong khoảng 0.012 đến 0.013 được khuyến nghị dùng trong thiết kế. Khi sử dụng các giá trị nn thấp này, người thiết kế cần đảm bảo không có phần tử gây nhám nổi bật như gân bên trong hoặc mối nối kém chất lượng.
B.1. Giá trị Manning’s n cho các loại cống
| Loại cống | Độ nhám hoặc dạng gân | Giá trị Manning’s n | Tài liệu tham khảo |
|---|---|---|---|
| Ống bê tông | Trơn | 0.010 – 0.011 | Straub et al. 1960, May et al. 1986, Tullis 1986 & 1991a |
| Hộp bê tông | Trơn | 0.012 – 0.015 | FHWA 1961 |
| Ống kim loại gân có sống xoắn | Trơn | 0.012 – 0.013 | Tullis 1983 & 1991b |
| Ống kim loại gân (Gân xoắn 2-2/3 in × 1/2 in / 68 × 13 mm) | 0.011 – 0.023 | FHWA 1980, Tullis 1991c | |
| Ống kim loại gân (Gân xoắn 6 in × 1 in / 150 × 25 mm) | 0.022 – 0.025 | FHWA 1980 | |
| Ống kim loại gân tròn hoặc mái vòm (Gân vòng 2-2/3 in × 1/2 in / 68 × 13 mm) | 0.022 – 0.027 | FHWA 1980 | |
| Ống kim loại gân tròn hoặc mái vòm (Gân vòng 5 in × 1 in / 125 × 25 mm) | 0.025 – 0.026 | FHWA 1980 | |
| Ống kim loại gân tròn hoặc mái vòm (Gân vòng 3 in × 1 in / 75 × 25 mm) | 0.027 – 0.028 | FHWA 1980 | |
| Ống kim loại kết cấu (Gân vòng 6 in × 2 in / 150 × 50 mm) | 0.033 – 0.035 | FHWA 1980 | |
| Ống kim loại kết cấu (Gân vòng 9 in × 2-1/2 in / 230 × 64 mm) | 0.033 – 0.037 | FHWA 1980 | |
| Polyethylene gân (corrugated) | Trơn | 0.009 – 0.015 | Barfuss & Tullis 1988, Tullis et al. 1990 |
| Polyethylene gân | Gân | 0.018 – 0.025 | Clyde 1980, USBR 1985 |
| Polyvinyl chloride (PVC) | Trơn | 0.009 – 0.011 | Neale and Price 1964, Bishop and Jeppson 1975 |
Chú thích:
- Các giá trị Manning’s n trong bảng này được xác định trong điều kiện phòng thí nghiệm và được hỗ trợ bởi tài liệu tham khảo đã nêu. Giá trị thực tế ngoài hiện trường có thể thay đổi do ảnh hưởng của mài mòn, ăn mòn, biến dạng và điều kiện mối nối.
- Xem Hình B.3, giá trị Manning’s n thay đổi theo kích thước thân cống.